Рекуррентная модель

В функционально-целевом подходе рекуррентная модель предметной области служит основой формализации главных задач структурно-алгоритмической организации автоматизированных систем и методов решения этих задач. Прежде чем перейти к рассмотрению модели, приведем основные определения, которые будут использоваться далее.

Одним из таких понятий является понятие <система>. В настоящее время существует множество определений этого понятия. В формальных исследованиях будем пользоваться определением [11]:

Системой 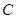называется отношение над абстрактными множествами X и Y:

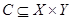, (3.1)

где 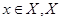- входное множество системы;

Отношением над множествами X и Y называется произвольное подмножество множества всехупорядоченных пар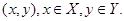

Система 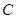определяется также с помощью задачи принятия решений: решающая система

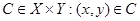
тогда и только тогда, когда 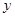является решением определенной задачи, конкретизация которой осуществляется посредством задания 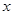. В работе [11] показано, что всякая система, формализованная посредством модели вход-выход (3.1), может быть представлена в виде решающей системы, и наоборот.

Пусть 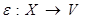- функция, отображающая произвольное множество 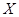в множество 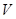, частично или полностью упорядоченное соотношением 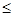. Задача оптимизации для системы (3.1) формулируется следующим образом. Дано подмножество 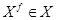. Требуется найти :

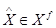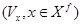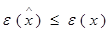
и (3.2)

Здесь 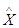- множество всех решений задачи оптимизации; 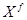- множество допустимых решений; 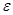- целевая функция; 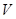- множество платежей. Элемент 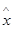, удовлетворяющий (3.2), называется решением оптимизационной задачи .

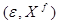Функция 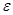может быть задана двумя функциями:

.

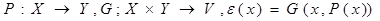В этом случае 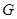называется оценочной функцией, или функцией (показателем) качества. Задача оптимизации тогда определяется тройкой 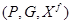или парой 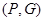, если .

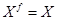Элементом системы будет называться простейшая неделимая с точке зрения решения конкретного класса задач часть системы. Под структурой системы понимается устойчивая упорядоченность в пространстве и времени ее элементов и связей. Множество элементов системы, определенных для конкретного класса решаемых задач, будет называться функциональным базисом, на котором строится эта система.

Понятия цели и целенаправленного поведения являются характерными для деятельности автоматизированных сметем. Общепринято понятие цели как предвосхищения результатов деятельности, это понятие и будет использоваться далее. Целенаправленное поведение предполагает выявление несоответствия между целью (целями) и реальной ситуацией. Цель достигается реализацией процесса преодоления этого несоответствия - организацией действий автоматизированной системы. Таким образом, под действием понимается процесс изменения внутреннего состояния и параметров выходов системы, направленный на решение стоящих перед ней задач.

В многоуровневых системах такие понятия, как <цель>, <целенаправленная деятельность> <целенаправленные системы>, тесно связаны с понятиями <принятие решений> и <системы принятия решений>. Целенаправленное поведение в сущности представляет собой последовательность принимаемых и реализуемых решений. Вследствие возможности представления систем типа вход-выход (3.1) в виде решающих систем и наоборот цели могут быть определены через решаемые задачи. Поэтому цель считается достигнутой, когда найдено решение соответствующей задачи (задача может быть оптимизационной). В дальнейшем в соотношение между целями и решаемыми задачами в работе будет вкладываться именно такой смысл.

Для решения задачи структурно-алгоритмического синтеза автоматизированной системы необходимо построить модель данной предметной области и соответствующую ей в определенном смысле модель автоматизированной системы на основе функционально-целевого подхода, задать критерии эффективности функционирования системы, определить механизм построения эффективных систем на базе предложенных моделей и выбранного критерия.

Как указывается, например, в работах [1,16] идеальная в смысле приспособленности к решаемой задаче по важнейшим характеристикам процесса решения структура вычислительной машины (системы) должна соответствовать естественной структуре решаемой задачи.

Следовательно, при организации управления в вычислительном эксперименте в общем случае нельзя обойтись только последовательно-параллельными композициями действий. Поэтому на уровне функциональных модулей пакетов прикладных программ (ППП) будем предполагать возможность организации более сложных конструкции, но это уже имеет место внутри элементов нижнего уровня (примитивов) древовидной декомпозиции, над которыми работает основанный на рекуррентных моделях аппарат синтеза. Тем не менее при построении систем на основе функционально-целевого подхода уровень применимости последовательно-параллельных конструкций может быть глубоким [5].

Иерархическая структура заложена в самом понятии комплексного вычислительного эксперимента, заведомо образуемого различными по характеру согласованными исследованиями различных сторон изучаемых объектов - объектно-ориентированными экспериментами. Каждый из этих экспериментов в свою очередь образуется набором исследований, основанных на различных методах изучения определенной стороны исследуемого объекта (эти методы в физическом эксперименте реализуются уже конкретными экспериментальными установками или комплексами установок). Такая детализация может продолжаться и далее.

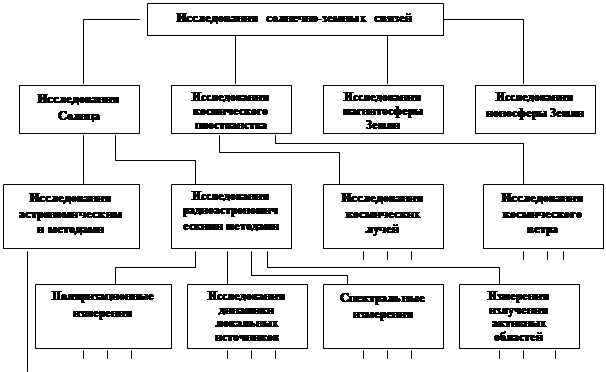
Для пояснения процесса иерархической декомпозиции задач комплексного вычислительного эксперимента рассмотрим исследования солнечно-земных связей. На рис.3.1 представлена общая схема декомпозиции понятия <комплексный эксперимент> в этой предметной области. Комплексный эксперимент является организованной совокупностью экспериментов по изучению солнечной активности, процессов в межпланетном космическом пространстве, параметров электромагнитного поля и ионосферы земли. Эти эксперименты образуют классы объектно-ориентированных экспериментов. Каждый из представителей этих классов в свою очередь разбивается на совокупность методо-ориентированных экспериментов.

На рис.3.1 показано, в частности, такое разбиение для радиоастрономических экспериментов по исследованию солнечной активности. Здесь к методо-ориентированным относятся эксперименты по исследованиям суммарного радиоизлучения солнца, динамики локальных источников, спектральных характеристик всплесков и т.д. Такое разбиение возможно вплоть до достижения неделимых с точки зрения исследователей подзадач, смысл которых будет ясен из дальнейшего изложения. Приведенная декомпозиция носит общий характер в реальных приложениях число уровней декомпозиции больше, это определяется необходимостью однозначной декомпозиции исходной задачи и конкретными неформализованными знаниями исследователей о структуре предметной области.

Обращаясь к соотношению между целями и решениями задач (если найдено решение задачи, в том числе и оптимизационной, то достигнута соответствующая цель), видим, что процесс последовательной детализация задачи в рассматриваемой предметной области комплексных исследований представляется деревом декомпозиции целей исследований (рис.3.1). Обратимся к задаче синтеза структуры многоуровневой системы управления вычислительными экспериментами, обеспечивающей достижение целей исследований. Такая задача имеет много аспектов. Определим, какими свойствами должны обладать отдельные элементы многоуровневой системы. Рассматриваемая ниже простая теорема о подсистемах многоуровневой системы показывает, что система в целом должна строиться из таких подсистем, которые обеспечивают покрытие соответствующих подзадач основной целевой задачи многоуровневой системы.

Теорема 3.1. Система, построенная из подсистем, покрывающих подзадачи основной целевой задачи системы, покрывает основную целевую задачу системы.

Доказательство. Пусть имеется некоторая декомпозиция основной целевой задачи 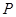системы 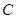на множество подзадач :

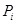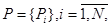
где 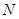— число подзадач основной целевой задачи системы. Декомпозиция проведена так, чтомножества подзадач не пересекаются:

,

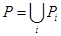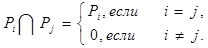(3.3)

Каждой подзадаче 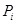поставим в соответствие некоторую подсистему 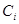системы 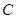, такую,

что совокупность действий 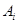, выполняемых этой подсистемой, будет покрывать подзадачу :

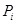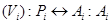покрывает .

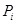Рис.3.1. Декомпозиция задач комплексных исследований в солнечно-земной физике.

Тогда объединение действий 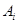всех подсистем будет покрывать объединение всех подзадач целевой задачи системы:

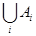покрывает , .

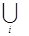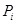Учитывая выражение (3.3), получаем, что множество действий, выполняемых подсистемами, покрывает основную целевую задачу системы:

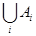покрывает .

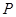Таким образом, доказано, что если строить систему 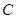из подсистем 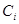, покрывающих подзадачи 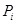, то множество действий 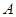системы 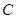покрывает множество целей 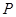тогда и только тогда, когда совокупность действий 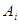подсистемы 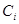покрывает множество соответствующих подцелей 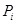для каждого . -

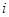Однако некоторая подзадача 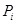может быть представлена в виде множества подзадач следующего уровня иерархии, т.е.

,

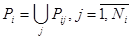где 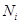- количество подзадач задачи 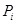. Следовательно, множество действий 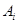покрывает множество задач 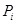тогда и только тогда, когда действия 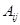подсистем 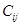покрывают соответствующие подцели 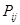для каждого 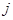, и так далее. Теорема доказана.

Следствие. Если строить декомпозицию системы изоморфно декомпозиция цели на подцели, то множество действий 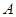системы 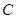покрывает множество целей 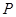тогда и только тогда, когда некоторое множество действии 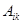подсистемы 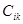покрывает множество подцелей 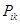на любом 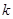-м уровне декомпозиции, включая нижний. Следовательно, вопрос о покрытии целей действиями можно решать длямелких подзадач и подсистем по отдельности, что значительно проще сделать.

Определив, что построение структуры системы должно проводиться изоморфно построению основной цели из некоторой совокупности подцелей, перейдем к построению формальной рекуррентной модели комплексных вычислительных экспериментов и систем управления этими экспериментами. Макроструктура многоуровневой системы управления вычислительным экспериментом в области исследований солнечно-земных связей, построенная изоморфно декомпозиции основной целевой задачи комплексных исследований, представляется в виде дерева, аналогично рис.3.1. Корню дерева ставятся в соответствие подсистема верхнего уровня (собственно система), вершинам дерева, отстоящим от корня на одно ребро, подсистемы, реализующие классы объектно-ориентированных экспериментов, на три ребра - подсистемы, реализующие методоориентированные эксперименты, и.т д.

Будем характеризовать любой элемент 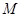макроструктуры системы состоянием 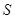, управляющим воздействием 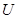для задания режима работы элемента и его состояния, входной информацией 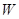. поскольку элементы макроструктуры - это программы, ориентированные на прием, переработку и передачу информации, то результатом работы элемента 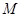является некоторая выходная информация 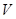. Будем рассматривать результирующую информацию 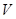как некоторую функцию от состояния элемента макроструктуры 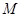, входной информации и управляющего воздействия:

.

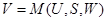Под элементарной неделимой единицей алгоритма управления экспериментом условимся понимать функциональную операцию 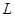- некоторую совокупность действий исполнительной системы, зависящих от управляющего воздействия, состояния элемента макроструктуры и его внутренней структуры:

.

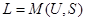Функциональные операции выполняют преобразование входной информации 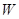в выходную следующим образом:

.

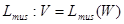Считывание состояния элемента макроструктуры достигается подачей специального управляющего сигнала :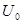

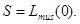
Таким образом определен алфавит функциональных операций (множество атомарных действийсистемы):

.

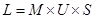Представим содержательную информацию рассматриваемой предметной области комплексных экспериментов в виде формальных высказываний. Построим алгебраическую систему 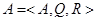, состоящую из непустого множества 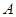, семейства алгебраических операций 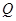и семейства отношений 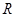. Для задания такой системы определим некоторые исходные объекты, которые будем рассматривать как неделимые; перечислим способы комбинирования исходных объектов между собой; укажем условие, которому удовлетворяют те и только те комбинации исходных объектов, которые считаются элементами системы; 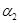сформулируем условие, при котором два элемента системы считаются равными.

Отождествим семейство 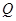алгебраических операций с организацией достижений совокупной цела исследований из известных атомарных целей, достижение которых реализуется атомарными действиями, заданными алфавитом 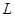. Такие совокупные цели обеспечиваются комбинациями последовательного и параллельного (одновременного) достижения атомарных целей, т.е. композициями элементов функционального алфавита целей, построенными с использованием двух обобщенных операций:

1) операция 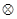: достичь атомарной цели 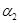после достижения атомарной цели ;

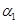2) операция 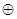: достичь атомарной цели 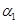одновременно с атомарной целью 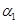. Использование принципа управления через целеполагание обеспечивает организацию всего многообразия вариантов комплексных вычислительных экспериментов через композиции элементов функционального алфавита, построенные с использованием двух введенных обобщенных операций. Действительно, совокупная цель достигается последовательно-параллельной комбинацией подцелей нижнего уровня.

Введем точно такие же операции для атомарных действий элементов функционального алфавита 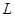. Зададим операцию. Как последовательное применение следующей функциональной операции к результату предыдущей:

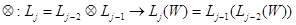. (3.4)

Операцию 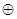зададим как одновременное выполнение двух атомарных воздействий:

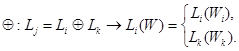(3.5)

Операция 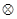производит последовательный запуск и исполнение выбранных атомарных элементов вычислительного процесса. Операция 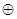производит параллельный запуск выбранных атомов.

Проведем исследования полученной алгебры строк (цепочек), определим свойства замкнутости, ассоциативности, коммутативности относительно введенных операци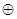й и 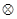а также установим наличие нулевого, единичного и обратных элементов. Не теряя общности, ограничим рассмотрение алгеброй действий, в которой нагляден физический смысл введенных обобщенных операций, Полученные результаты справедливы и для алгебры целей.

1. Замкнутость. Алгебра 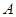является замкнутой относительно операци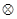й и 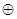,поскольку полученные новые элементы 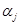являются также цепочками функциональных операций:

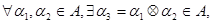
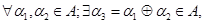
2. Ассоциативность. Операция 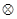является ассоциативной, поскольку совокупное воздействие на экспериментальную установку при последовательномвыполнении атомарных воздействийне зависит от группировки элементов, составляющих цепочку:

.

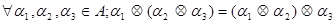Операция 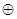также ассоциативна, поскольку совокупное воздействие при одновременном выполнении атомарных действий не зависит от группировки элементов, составляющих цепочку:

.

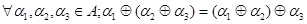3. Коммутативность. Операция 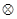некоммутативна, так как в результате изменения порядка элементарных действий изменяется физический смысл совокупного действия:

.

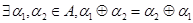Операция 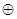коммутативна, поскольку при одновременном выполнении элементарных воздействий совокупное воздействие не зависит от порядка их выполнения:

.

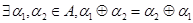4. Единичный элемент. Единичным элементом рассматриваемой алгебры является пустая цепочка 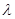, т.е. цепочка, не производящая никаких действий с экспериментальной установкой:

.

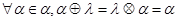5. Нулевой элемент. Нулевым элементом рассматриваемой алгебры является цепочка 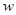, производящая блокировку действий элемента макроструктуры, выполняющего эту цепочку:

,

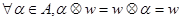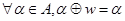
Последовательное включение (операция 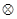в цепочку выполняемых действий 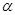нулевого элемента приводит к блокировке процесса выполнения всей цепочки 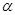. Параллельное вылолнение (операция?) нулевого элемента одновременно с цепочкой 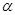не влияет на ее выполнение.

6. Обратные элементы. Для операции 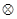не существует такой цепочки 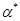, последовательное применение которой после цепочки 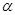давало бы в результате единичный элемент алгебры 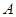(пустую цепочку 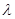). Для операции 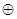не существует такой цепочки 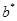, параллельное выполнение которой вместе с цепочкой 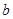давало бы в результате нулевой элемент рассматриваемой алгебры (атом блокировки действий ).

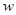Следовательно, можно сделать вывод, что алгебра 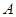является полукольцом, так как имеет

полугрупповые свойства по операциям 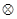и выполняется свойство дистрибутивности

.

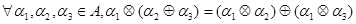Зададим на алгебре цепочек 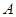некоторое отношение эквивалентности 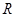. Отношение эквивалентности может задаваться как совпадение параметров цепочек (например, длины или используемых операций) либо как совпадение параметров результата, т.е. при одинаковой входной информации в результате выполнения двух разных цепочек получаем результирующую информацию, принадлежащую в обоих случаях к одному некоторому множеству.

Известно, что заданное некоторым образом отношение эквивалентности 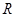разбивает все множество цепочек на множество непересекающихся классов эквивалентности [10]. Поэтому все семантически одинаковые цепочки находятся в пределах одного класса эквивалентности. Классы эквивалентности 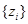характеризуются следующими соотношениями:

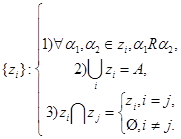
В каждом классе эквивалентности задается новое отношение эквивалентности, разбивающее каждый класс эквивалентности на подклассы, и т. д. В результате получается семейство алгебр классов эквивалентности

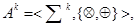
где 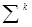- множество цепочек над алфавитом .

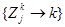Таким образом строятся модели декомпозиции целей исследований на комплексной предметной области и декомпозиция действий соответствующей автоматизированной системы, обеспечивающих достижение этих целей. Они получены абстрагированием от конкретного содержания составляющих предметных областей и заменой их понятием классов эквивалентности функций (целей или действий в зависимости от приложения модели), т.е. множеств функций, эквивалентных в смысле их предметной направленности. В каждом классе эквивалентности задано новое отношение эквивалентности, относящее функции к разным поднаправлениям и разбивающее каждый класс эквивалентности на подклассы. Рекуррентный процесс детализации исходной функции продолжается вплоть до достижения уровня <примитивов> - элементарных функций, неделимых с точки зрения исследователя. Тем самым задание множества отношений эквивалентности функций определяет топологию на множестве функций. Базой этой топологии является множество примитивов.

Полученная декомпозиция предметной области представляется древовидным графом иерархии классов, в котором узлы - имена классов, ребра - отношения включения, корень - имя функции на комплексное предметной области, листья - примитивы:

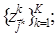
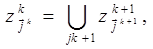
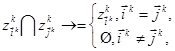(3.6)

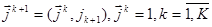
где 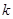- индекс уровня декомпозиции; 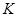- число уровней; 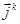— вектор-индекс длиной 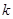класса эквивалентности на 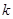-м уровне декомпозиции; 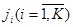- -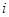й компонент вектор-индекса; 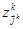- имя класса на 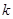- м уровне декомпозиции с вектор-индексом 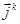. Система (2.6) порождается системой отношений эквивалентности

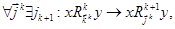. (3.7)

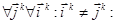
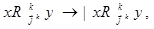
где 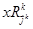- отношение эквивалентности, разбивающее 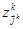на

.

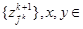
Построенная алгебраическая система 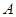, состоящая из множества элементов, двух алгебраических операций и семейства отношений эквивалентности, является формальной моделью. Постановки и решения задач организации вычислительного эксперимента, поскольку одинаковым образом описывает цели эксперимента и действия по достижению этих целей на любом уровне декомпозиции исходной задачи.

В общем случае имеется множество классов эквивалентности

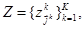
(3.8)

где 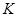- число уровней декомпозиции; соответственно общая рекуррентная модель представляет собой иерархию алгебр

,

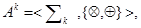гомоморфно отображенных друг на друга <снизу вверх>:

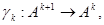(3.10)

где 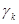есть совокупность отношений .

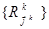Таким образом, построены формальная рекуррентная модель предметной области (комплексных научных исследований), основанная на рекуррентной декомпозиции целей исследований, и модель соответствующей системы управления вычислительным экспериментом в этой предметной области, основанная на адекватном декомпозиции целей процессе детализация действий по организации и проведению эксперимента.

Date: 2015-07-02; view: 1286; Нарушение авторских прав