Основні властивості вибіркової середньої

1. При множенні усіх варіант вибірки на однаковий множ­ник вибіркова середня також множиться на цей множник.

2. Якщо додати (відняти) до всіх варіант вибірки однакове число, то вибіркова середня зростає (зменшується) на це число.

Ці властивості можна поєднати в одну формулу, яку нази­вають формулою моментів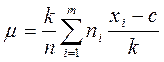

56.Генеральною середньою Dг наз середнє арифметичне квадратів відхилень значень ознак генеральної сукупності від їх середнього значення. Вибірковою дисперсією D_B назива­ють середню квадратів відхилення варіант від вибіркової середньої з врахуванням відповідних частостей . Вибірковим середньоквадратичним відхиленням (стандартом) називають квадратний корінь із вибіркової дисперсії. Вибіркова дисперсія дає занижені зна­чення для дисперсії D (X) генеральної сукупності, вона буде зсунутою оцінкою D(Х). Тому вибіркову дисперсію доцільно виправити таким чи­ном, щоб вона стала незсунутою оцінкою.

57. вібіркова дисперсия D_в наз. Середню квадратів відхилення варіант від вибіркової середньої з врахуванням відповідних частостей. 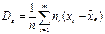²

Виправлене середньоквадратичне відхилення s=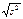

58. точковими оцінками параметрів розподілу генеральної сукупності наз. Такі оцінки, які визначаються одним числом.

Інтервальна оцінка та, що визначається 2 числами – кінцями інтервалу.

Надійністю оцінки параметрів 0 за 0^* наз. імовірність 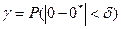з якою викон. нерівність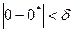

Інтервал (0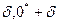^* - )= наз. надійним, якщо він покриває невідомий параметр 0 із заданою надійністю .

Точність оцінки визнач. .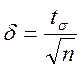

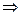
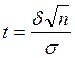
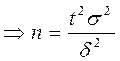
59. 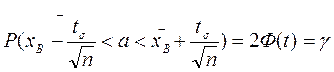, тобто з надійністю 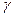довірчий інтервал (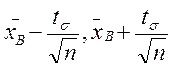) покриває невідомий параметр а. точність оцінки буде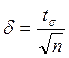

Число t визначається рівністю 2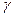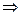Ф(t)= Ф(t)= .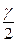

При зростанні об’єму вибірки число 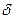зменш., а це знач., що точність оцінки збільш. Коли надійність збільш. 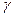, ф-ція Ф(t) зростає. Збільшення надійності зменш. її точність.

60. 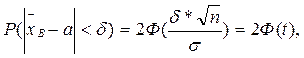де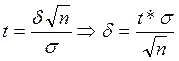

Ф-інтегральна ф-ція Лапласа, 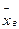-випадкова величина.

61. мода- значения варіанти, яка має найбільшу частоту.

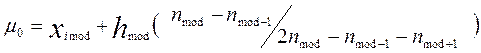
медіана значення змінюваної ознаки, яке ділить множину даних навпіл, так що одна половина значень більша від медіани, а друга – менша.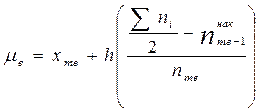

Початковий момент середнє знач. К-го степення різниці х_і-с, при с=0 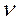^*_k=

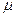центральний момент середнє знач. К-го степення різниці х_і-с, при с= М[(X-m_k)^k]= _k

асиметрія: 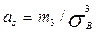, де m₃-централ. емпіричний момент 3-го порядку.

Ексцес: е_к=m₄/ 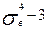, m₄- централ. емпіричний момент 4-го порядку.

Дати означення емпіричної та теоретичної частоти, записати формули обчислення теоретичної частоти для розподілів: а) Пуассона, б)Нормальної генеральної сукупності. Пояснити зміст букв. Навести загальну схему побудови відповідних графіків. Навести приклад вирівнювання статистичних рядів в припущенні, що генеральна сукупність розподілена за законом: а) Пуассона, б) нормальним.

Розглянемо ДВВ Х, закон розподілу якої невідомий, нехай виконано п випробувань. В яких величина Х прийняла п1 разів значення х1, п2 разів значення х2,... пк разів значення хк. Причому сума: ∑пі=п. Емпіричними частотами називають частоти пі, що спостерігають фактично. Теоретичними частотами називають частоти, що знаходяться теоретично (розрахунково). Теоретичні частоти знаходять за формулою: пі=п*Рі (п – кількість випробувань; Рі – імовірність хі).

Пуссона: Рп(к)=(λ^k*e^-λ)/к!. λ- середня вибіркова.

63. Дати означення функціональної, статистичної та кореляційної залежності, умовного середнього, вибіркових рівняння та лінії регресії. Навести приклади. Розглянемо залежність У від однієї випадкової величини Х, а потім від декількох величин. Дві випадкові величини можуть бути пов’язані функціональною залежністю або залежністю іншого роду, яка називається статистичною, або бути незалежними. Строга функціональна залежність реалізується рідко. У цьому випадку виникає статистична залежність. наприклад: якщо У залежить від Z1, Z2, V1, V2, а Х залежить від Z1, Z2, і U1. то між У і Х є статистична залежність (наявні спільні фактори Z1, Z2). Статистичною називають залежність при якій зміна однієї з величин викликає зміну розподілу іншої. Зокрема, статистична залежність проявляється в тому, що при зміні однієї з величин змінюється середнє значення іншої. В цьому випадку статистичну залежність називають кореляційною. Умовним середнім Ух(з рискою зверху) називають середнє арифметичне значень У, відповідних значенню Х=х. Кореляційною залежністю У від Х називають функціональну залежність умовної середньої Ух(з рискою зверху) від х: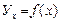

Це рівняння називають рівнянням регресії У на Х. Функцію f(x) називають регресією У на Х, а її графік – лінією регресії У на Х вибіркове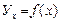

64. вивести формули для обчислення параметрів вибіркового рівня лінійної регресії: а) за не згрупованими данними. Б) за згрупованими данними кореляційної таблиці. Пояснити зміст букв, навести приклади. Дана формула виведена із рівняння прямої: у=кх+b. Де к замінено на вибірковий коефіцієнт регресії. Вибіркове рівня лінійної регресії: 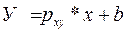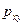- вибірковий коефіцієнт регресії У на Х.

Записати формули для обчислення вибіркового коефіцієнта кореляції, кінців надійного інтервалу для інтервальної оцінки коефіцієнта кореляції нормально розподіленої генеральної сукупності. Навести найпростіші приклади нелінійної кореляції, дати поняття множинної кореляції.

Вибіркового коефіцієнта кореляції:

67. дати означення статистичної гіпотези. Назвати основні види статистичних гіпотез. Дати означення нульової (основної), альтернативної (конкурентної) гіпотез. Дати означення помилки першого роду, другого роду. Навести приклади. Статистичною називають гіпотезу про вид невідомого розподілу чи про параметр відомих розподілів. Існує два види гіпотез. Нульовою (основною) називають гіпотезу Н_0, ту що висувають. Конкурентною (альтернативною) називають гіпотезу Н₁, яка суперечить нульовій. Помилка 1-го роду полягає в тому, що буде відкинута правильна гіпотеза. Помилка 2-го роду полягає в тому, що буде прийнята неправильна гіпотеза.

68. Статистичним критерієм узгодження перевірки гіпотези (або просто критерієм) називають випадкову величину К, розподіл якої (точний або наближений) відомий і яка застосовується для перевірки основної гіпотези.

Спостереженим значенням критерію узгодження називають значення відповідного критерію, обчислене за даними вибірки.

Критична область. Критичні точки.+

Після вибору стат.критерію К вся множина його можливих значень розбивається на 2 підмножини, що не перетинаються. Одна з них містить ті з-ня К, при яких гіпотеза Но приймається і назив. областю прийняття гіпотез. Інші області, що відхиляються називаються критичними областями.

Ці області відділяються точками, які назив. критичними точками(Kkp).

Розрізняють однобічну (правобічну та лівобічну) та двобічну критичні області.

Правостороння критична область:

К>Kkp> 0

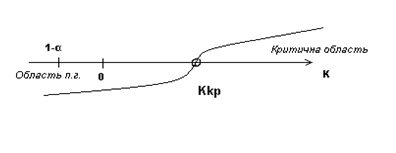
Лівостороння критична область:

0<Kkp<K

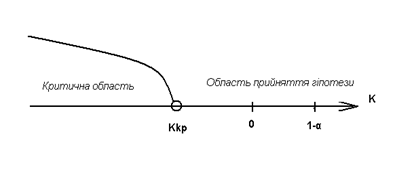
Двостороння критична область:

K<Kkp’<0 U K>Kkp”>0

Date: 2015-07-01; view: 576; Нарушение авторских прав