Довести основні властивості математичного сподівання і дисперсії

Основні властивості математичного сподівання

1) Математичне сподівання постійної величини дорівнює самій постійній М(С) = С.

2) Постійний множник можна виносити за знак математичного сподівання М(СХ)=С*М(Х).

3) Математичне сподівання добутку декількох взаємно незалежних дискретних випадкових величин дорівнює добутку їх математичних сподівань, тобто М(Х₁*Х₂*…*Х_n) = М(Х₁)*М(Х₂)*…*М(Х_n).

4) Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань, тобто М(Х₁+Х₂+…+Х_n) = М(Х₁)+М(Х₂)+…+М(Х_n)

Основні властивості дисперсії.

1)Дисперсія будь-якої ДВВ Х невід’ємна

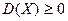
Дійсно, (Х – М(Х))² невід’ємна, тому згідно означення математичного сподівання та властивостей p_k, k =1,2, …, n, D(X) також невід’ємна.

2)Дисперсія постійної величини С дорівнює нулеві

D(X) = 0

Дійсно, якщо Х=С, то М(С)= С, тому С – М(С) = 0

3)Постійний множник С можна виносити за знак дисперсії, при цьому постійний множник треба піднести у квадрат

D(СX) = С² D(X).

Дійсно, СХ – М(СХ) = С (Х – М(Х)), тому

(СХ – М(СХ))² = С² (Х – М(Х))².

Постійний множник С² можна виносити за знак математичного сподівання, тому з формули D(X) = М((Х – М(Х))²) випливає потрібна рівність D(СX) = С² D(X).

4) Дисперсія ДВВ Х дорівнює різниці між математичним сподіванням квадрата випадкової величини Х та квадрата її математичного сподівання

D(X) = М(Х²) – (М(Х))².

Дійсно, D(X) = М((Х – М(Х))²) = М(Х² – 2ХМ(Х) + М²(Х)) = М(Х²) – 2М²(Х) + М²(Х) = М(Х²) - М²(Х).

5) дисперсія алгебраїчної суми ДВВ Х та Y дорівнює сумі їх дисперсій

.

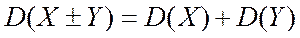Записати основні закони розподілу д.в.в.: а) біноміальний; б)Пуассона; в)геометричний; г) гіпергеометричний. Пояснити зміст букв. Навести приклади д.в.в., розподілених за цими законами.

1. Біноміальний

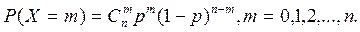
2.Пуассона

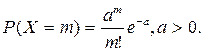
3.Геометричний

.

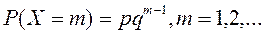4. Гіпергеометричний

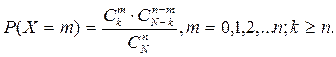
Date: 2015-07-01; view: 369; Нарушение авторских прав