Функция готовности

Если время до отказа и время ремонта представляют независимые случайные величины, распределенные каждая по экспоненциальному закону, то подобный подход приводит к марковскому процессу, называемому процессом «гибели и размножения» [7].

Для необслуживаемых систем важны два критерия качества:

- функция надежности, которая определялась вероятностью безотказной работы к некоторому моменту времени t (то есть переход в поглощающее состояние не происходит до момента t);

- среднее время, которое необходимо до первого попадания в поглощающее состояние (состояние отказа), или, как его называют, среднее время до первого отказа.

Для обслуживаемых систем обычно представляют интерес два других критерия. Первым является время, в течение которого система находится в исправном состоянии, или состоянии готовности. Как будет показано ниже, процесс гибели и размножения описывает готовность системы в переходном и установившемся режимах. Для систем, которые должны работать длительное время непрерывно, изучение установившегося режима является достаточным.

Другим критерием качества, относящимся к обслуживаемым системам, является среднее время возвращения. В этом случае нас интересует время до возвращения системы в исправное состояние из состояния отказа. Иногда его называют средним временем одного вынужденного простоя. Важность среднего времени возвращения ясна, так как готовность учитывает только общее время, проведенное системой в исправном состоянии, и не указывает, как это время распределено.

Метод определения вероятности того, что система находится в некотором состоянии в момент времени t+Δt, остается тем же, что и для необслуживаемых систем. Единственное отличие состоит в том, что в связи с возможностью ремонта система может осуществлять прямые и обратные переходы вместо односторонних переходов в случае необслуживаемых систем. Так, для системы из одного образца оборудования можно ввести два состояния: состояние 0, когда система работает, и состояние 1, когда система неисправна и ремонтируется. Далее, так как условная вероятность отказа в интервале t, t+Δt равна λΔt, а условная вероятность завершения ремонта в интервале [ t, t+Δt ] равна µΔt, получаем следующую матрицу переходов:

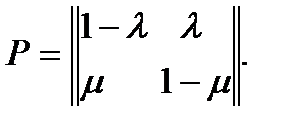(5.16)

Конечно, разностные уравнения, описывающие стохастическое поведение этой системы, можно составить из следующих соображений: вероятность того, что система находится в состоянии 0 к моменту t+Δt, выводится из вероятности того, что эта система была в состоянии 0 в момент времени t и не отказала в течение отрезка времени [ t, t+Δt ], или что она находилась в состоянии 1 в момент t и возвратилась в состояние 0 за интервал t, t+Δt. Поэтому получаем

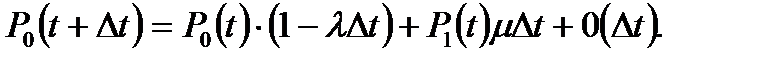(5.17)

Подобным образом, вероятность пребывания систем в состоянии 1 в момент времени t+Δt выводится из вероятности того, что данная система была в состоянии 1 в момент t и ремонт за время [ t, t+Δt ] не был закончен. Поэтому

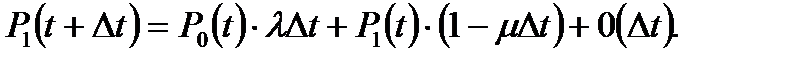(5.18)

Член 0(Δt) в обоих уравнениях представляет собой вероятность осуществления двух событий за [ t, t+Δt ], то есть является бесконечно малой величиной более высокого порядка, чем остальные величины.

Заметим, что коэффициенты этих уравнений являются элементами одних и тех же строк матрицы переходов. Как и ранее, дифференциальные уравнения получаем, используя предельный переход при Δt →0, также определения

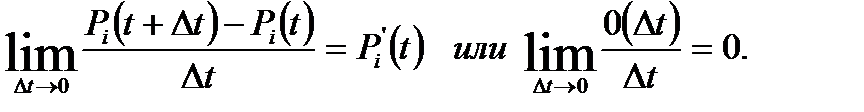(5.19)

В результате имеем 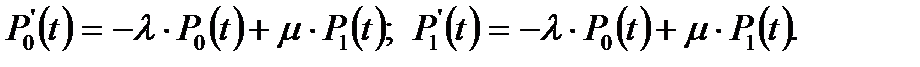(5.20)

Если система при t =0 находилась в работе, то начальными условиями будут Р(0) =1, Р₁(0) =0.

Интересно также рассмотреть случай, когда при t =0 система находится в ремонте. Тогда начальными условиями будут Р(0) =0, Р₁(0) =1. Применяя преобразование Лапласа и учитывая начальные условия Р(0) =1, Р₁(0) =0, получаем

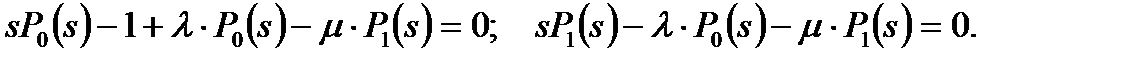(5.21)

После приведения подобных членов имеем:

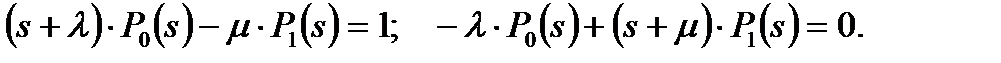(5.22)

Хотя P₀(s) и P₁(s) для этого случая можно легко найти подстановкой, используем правило Крамера, так как это окажется полезным для дальнейшего изложения [7]. Для решения данной системы уравнений введем определитель D, элементами которого являются коэффициенты при P_i(s). Кроме того, введем определитель D_i, который образуется в результате замены i -го столбца столбцом коэффициентов правой части уравнений системы. Тогда 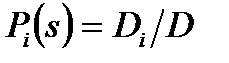и

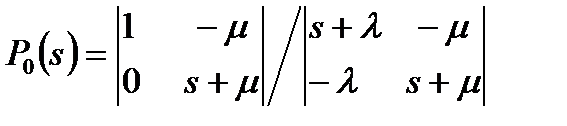или 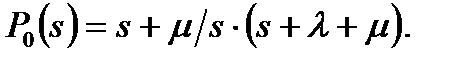(5.23)

Функция готовности, которую обозначим через A(t), является обратным преобразованием Лапласа для P₀(s), то есть

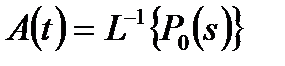или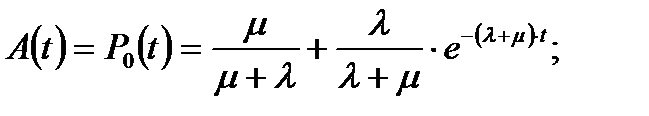

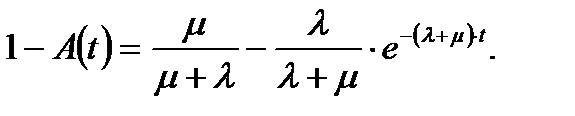(5.24)

Если система в начальный момент t =0 находилась в ремонте, то есть Р₀(0) =0 и Р₁(0) =1, то

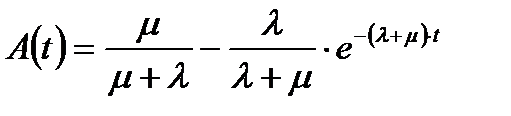и 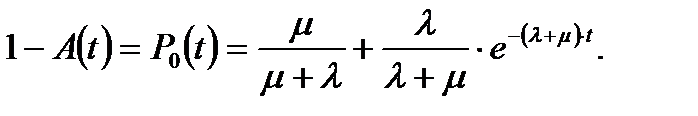(5.25)

Заметим, что при больших значениях t выражения (5.24) и (5.25) становятся равными. Это означает, что после того, как система проработает некоторое время, ее поведение становится независимым от начального состояния.

Функцию готовности A(t) можно понимать как вероятность того, что система находится в рабочем состоянии в произвольный момент времени t. Во многих случаях нас интересует среднее время исправного для некоторого конечного интервала времени. Тогда можно просуммировать A(t) по всему интервалу и разделить на него, то есть

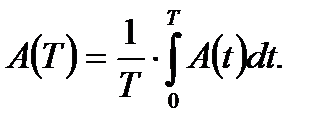(5.26)

В данном случае 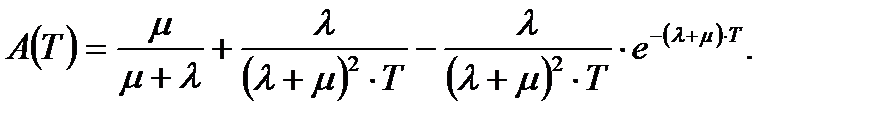(5.27)

Если нас интересует коэффициент готовности системы при длительной эксплуатации, то, полагая T→∞, имеем

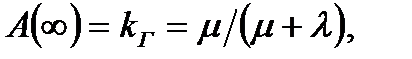(5.28)

причем 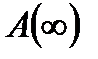обычно называют коэффициентом готовности в установившемся режиме. Этим предполагается, что для большой совокупности (ансамбля) одинаковых образцов оборудования процесс будет поддерживаться в состоянии статического равновесия.

В литературе по вопросам надежности можно часто встретить определение коэффициента готовности как отношения среднего времени до отказа к сумме среднего времени до отказа и среднего времени ремонта. Для рассматриваемой системы такое определение приводит к результату, аналогичному выражению (5.28). Однако, как далее будет видно, для резервированных систем эта эквивалентность не сохраняется. Для системы из одного образца оборудования среднее время до отказа равно 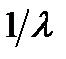, среднее время ремонта 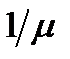и коэффициент готовности .

Для всех случаев, когда оказывается возможным перейти из одного состояния в другое в течение длительного периода времени, легко показать, что 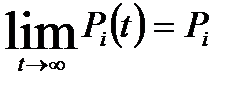всегда существует. Это означает, что решение для установившегося режима можно получить, полагая производные 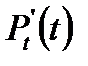равными нулю. Тогда система дифференциальных уравнений сводится к системе алгебраических уравнений. Для решения этих уравнений нужно использовать тот факт, что P_i (i =0, 1, 2, ….., n) составляют распределение вероятностей, то есть . Так, рассматриваемая система уравнений приобретает следующий вид:

(5.29)

Откуда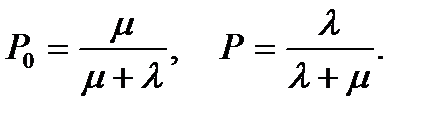

Date: 2015-07-01; view: 873; Нарушение авторских прав