Гипербола және оның қасиеттері

Анықтама. Гипербола деп фокустары деп аталатын нүктелерден қашықтықтары айырмасының модулі сол фокустары арақашықтығынан (F₁F₂ = 2c) кем болатын тұрақты 2 а санына тең болатын жазықтықтағы нүктелердің геометриялық орнын айтады, оны былайша белгілейді:

|F₁М - F₂М| = 2 а (5).

F₁, F₂ – гиперболаның фокустары. F₁ = (-c; 0); F₂(c; 0), F₁F₂ = 2c.

с – фокустары ара қашықтығының жартысы; 2 а - тұрақты шама. F₁М және F₂М қашықтықтарын r₁ = F₁М, r₂= F₂М деп белгілесек, онда (5) теңдік мына түрде жазылады:

ïr₁ – r₂ï= 2a (5¹)

Гиперболаның бойынан кез келген М(х, у) нүкте алайық..

y

M(x, y)

b

r₁

r₂

x

a

F₁ А₂(- а;0) А₁(а;0) F₂

c

Сонда:

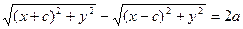
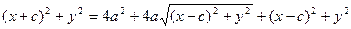
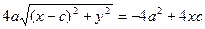
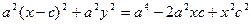
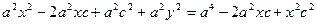
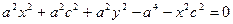
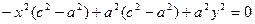
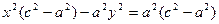
с² – а² = b² деген белгілеме енгіземіз (геометриялық түрдегі бұл шама – кіші жарты ось)

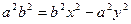
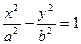
Гиперболаның жабайы (канондық) теңдеуін алдық..

Гипербола фокустарын қосатын кесіндінің ортасына (О нүктеге), және координат осьтеріне қарағанда симметриялы.

2а гиперболаның нақты өсі деп аталады.

2b гиперболаның жорамал өсі деп аталады.

Гиперболаның қасиеттерін студенттерге өз беттерімен қарастыруға тапсырылады.

Гиперболаның екі асимптотасы болады және олар 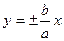теңдеулері арқылы беріледі.

Анықтама. 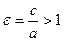қатынасы гиперболаның эксцентриситеті деп аталады, мұндағы с – фокустары қашықтығының жартысы, а –нақты жарты өсь.

с² – а² = b² екеніні ескерсек:

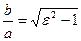
Егер а = b, = 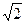болса, онда гипербола теңбүйірлі (тең қабырғалы) деп аталады.

Анықтама. Гиперболаның нақты өсіне перпендикуляр, оның центріне қарағанда симметриялы және одан a/ қашықтықта болатын екі түзу гиперболаның директрисалары деп аталады.Олардың теңдеулері: .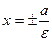

Теорема. Егер r – гиперболаның кез келген М нүктесінен қандай да бір фокусына дейінгі қашықтығы, ал d – осы фокусқа сәйкес директрисаға дейінгі қашықтығы болса,онда r/d қатынас – эксцентриситетке тең тұрақты шама.

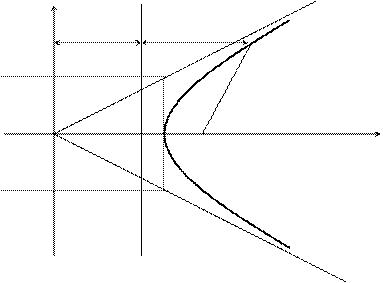
Дәлелдеуі. Гиперболаны схемалық түрде кескіндейік:

y

a/e d

M(x, y)

r₁

0 a F₁ x

OF₁ = c. Геометриялық кескінедемеден мыналарды жазуға болады:

a/ e + d = x, сондықтан d = x – a/ e. (x – c)² + y² = r²

Гиперболаның канондық теңдеуінен: 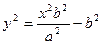, с учетом b² = c² – a²:

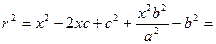
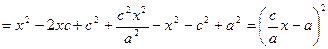
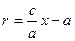
Сонда с/a = болғандықтан, r = x – a.

Сонымен: .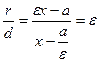

Гиперболаның сол жақтағы тармағы үшін дәлелдеме осы тәріздес.

Пример. Төбелері мен фокустары 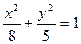эллипсінің сәйкес төбелері мен фокустарында болатын гиперболаның теңдеуін жаз.

Эллипс үшін: c² = a² – b².

Гипербола үшін: c² = a² + b².

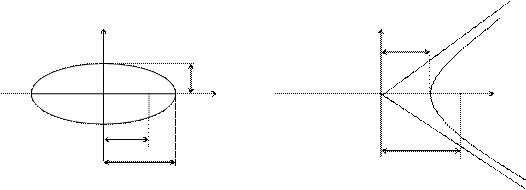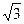
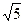
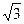
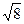
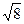
Гиперболаның теңдеуі: .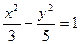

Мысал. Егер гиперболаның эксцентриситеті 2-ге тең, ал фокустары 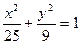теңдеуімен берілген эллипстің фокустарымен беттессе, онда гиперболаның теңдеуін жаз.

Шешу. Эллипстің фокустық ара қашықтығын табамыз: c² = 25 – 9 = 16.

Гипербола үшін: c² = a² + b² = 16, = c/a = 2; c = 2a; c² = 4a²; a² = 4;

b² = 16 – 4 = 12.

Сонда 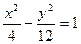- гиперболаның теңдеуі болады.

Date: 2015-07-01; view: 1699; Нарушение авторских прав