
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Связь между алгеброй логики и двоичным кодированием
|
|
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже две: "1" и "0".
1. Основные понятия математической логики
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности и ложности) и логических операций над ними.
Создателем алгебры логики является английский математик Джордж Буль (XIX век), в честь которого эта алгебра названа булевой алгеброй высказываний.
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Для обозначения истины (истинного высказывания) используется символ 1, а для обозначения лжи (ложного высказывания) используется символ 0. Привести примеры ложных и истинных высказываний.
Рассмотрим примеры логических высказываний (см. Таблицу 1):
Таблица 1. Примеры логических выражений
| Предложение | Характеристика с точки зрения алгебры логики |
| Москва - столица России | Истинное логическое высказывание |
| За днем наступит вечер | Истинное логическое высказывание |
| В Москве проживают только граждане России | Ложное логическое высказывание |
| После дождя всегда тепло | Ложное логическое высказывание |
| После вторника будет выходной | Не является логическим высказыванием, (если у человека текущий график работы) |
Слова и словосочетания «не», «и», «или», «если…то», «тогда и только тогда» называют логическими связками. Высказывания бывают элементарные и составные.
Москва - столица России - Элементарное высказывание.
Если у учащегося хорошая успеваемость и мало пропусков занятий, то он проходит практику на производстве - Составное высказывание.
Пример обозначения логических высказываний.
А – высказывание «В четверг был дождь»,
В – высказывание «В пятницу было солнечно», то составное высказывание «В четверг был дождь, а в пятницу было солнечно», можно записать в виде:
А и В.
Здесь А, В – логические высказывания (могут быть либо истинными, либо ложными), и – логическая связка.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (см. Таблицу 2): Таблица 2. Логические связки
| № | Логическая связка | Название | Обозна-чение | Высказы-вание | Математическая запись |
| и | конъюнкция логическое умножение | Ù, & *, And | A и В | A Ù B, A & B A * B, A And B | |
| или | дизъюнкция логическое сложение | Ú +, Or | A или В | A Ú B A + B, A Or B | |
| не | инверсия, логическое отрицание | , 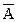 ,
Not ,
Not
| не А | А, 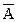 ,
Not A ,
Not A
| |
| Если…то | импликация, логическое следование | →, Þ | Если A, то В | A → B A Þ B | |
| тогда и только тогда | эквивалентность, равносильность, логическое тождество | «, º Û, ~ | А тогда и только тогда, когда В | А«В, АºВ АÛВ, А~В |
Импликацию можно выразить через дизъюнкцию и отрицание:
| A → B = А Ú B | (1) |
Эквивалентность можно выразить через отрицание, дизъюнкцию и конъюнкцию:
| A «B = (А Ú B) Ù (B Ú А) | (2) |
Вычисление значения логического выражения производится слева направо в соответствии с таблицей истинности (см. Таблицу 3) и приоритетом выполнения логических операций (см. Таблицу 4). Порядок выполнения операций можно менять, используя круглые скобки.
Таблица 3. Таблица истинности
| A | B | A Ú (+)B | A Ù (*)B | A |
При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
- действия в скобках
- инверсия (отрицание);
- конъюнкция (умножение);
- дизъюнкция (сложение):
- импликация (следование)
- эквивалентность (равносильность).
Date: 2015-07-01; view: 1094; Нарушение авторских прав