
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Взаимное пересечение многогранников
|
|
Линия пересечения двух многогранников может быть построена двумя способами.
Первый способ состоит в определении точек пересечения ребер первого многогранника с гранями второго многогранника и ребер второго с гранями первого, т.е. задача сводится к многократному решению задачи по определению точки пересечения прямой с плоскостью.
Второй способ состоит в определении линий пересечения граней одного многогранника с гранями другого. Задача сводится к определению линии пересечения двух плоскостей. Преимущество отдается тому из способов, который в зависимости от условия задания дает наиболее простое и точное решение. Эти два способа построения линии пересечения двух многогранников часто комбинируют между собой.
Линия пересечения двух многогранников представляется в общем случае в виде пространственных замкнутых ломаных линий. В зависимости от вида многогранников и их взаимного расположения линией пересечения может быть одна, две и более ломаных линий (в частности могут быть и плоские ломаные линии). Отрезки ломаных линий являются отрезками прямых, по которым пересекаются грани двух многогранников. Вершины ломаной линии этой точки пересечения ребер одного многогранника с гранями другого, и ребер второго с гранями первого. Отрезки ломаной линии строятся как отрезки прямых, соединяющих только те пары вершин, которые принадлежат одной и той же грани первого многогранника, а также одной грани второго многогранника. Вершины ломаной линии соединяются при строгом соблюдении последовательности.
Задача: Построить линию пересечения прямой четырехугольной призмы с треугольной пирамидой (рис.5.9).
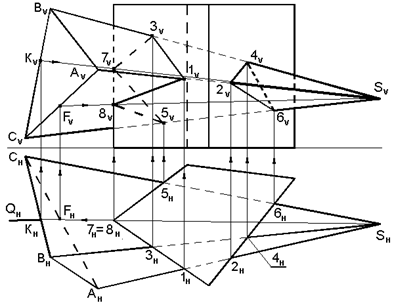
Рис. 5.9. Построение линии пересечения пирамиды и
призмы
Решение:
Призма своим основанием стоит на горизонтальной плоскости проекций Н. Горизонтальные проекции ее вертикальных ребер вырождаются в точки. Грани боковой поверхности призмы проецируются в отрезки прямых. Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника. Так, ребро SA пирамиды пересекается с двумя вертикальными гранями призмы в точках 1 (1V,1H) и 2 (2V,2H).
Ребро SB пирамиды пересекает две вертикальные грани призмы в точках 3(3V,3H) и 4(4V, 4H) и ребро SC – в точках 5(5V, 5H) и 6(6V, 6H). Из четырех вертикальных ребер призмы только одно пересекает пирамиду. Находим точки его пересечения с гранями пирамиды. Через это ребро и вершину S пирамиды проводим вспомогательную горизонтально проецирующую плоскость Q. На рис.5.9 показан горизонтальный след этой плоскости QH. Плоскость Q пересекает пирамиду по двум прямым линиям SK и SF, которые пересекаются с ребром призмы в точках 7(7V, 7H) и 8(8V, 8H). Последовательность построения точек 7V и 8V на рис.5.9 показана с помощью стрелок.
Соединяя каждые пары точек, принадлежащих одной и той же грани, получаем две ломаные линии пересечения многогранников. Одна из них пространственная ломаная линия 137581, другая – треугольник 246 – плоская ломаная линия лежащая в грани призмы. Видимость линии определяем с помощью конкурирующих точек.
Date: 2015-07-01; view: 962; Нарушение авторских прав