Способ вращения вокруг линии уровня

Этот способ удобно применять в тех случаях, когда требуется расположить плоскую фигуру параллельно плоскости проекций, что достигается за один поворот.

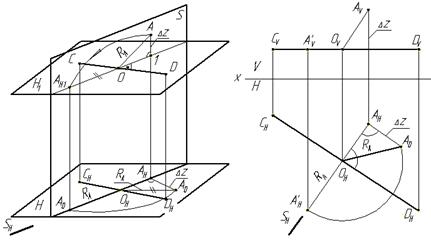
Рассмотрим сущность способа на примере поворота точки А вокруг горизонтали (Рис.4.13а).

Возьмем в пространстве точку А и горизонталь СД и повернем точку А вокруг СД до положения, когда она окажется в горизонтальной плоскости Н₁, проходящей через СД. Траекторией точки А будет окружность R=ОА, центр О которой лежит на прямой СД. Плоскость окружности, то есть плоскость S вращения точки А перпендикулярна к прямой СД – оси вращения, а следовательно и к плоскости Н. Поэтому горизонтальная проекция А будет перемещаться по горизонтальному следу S_Н плоскости вращения, перпендикулярному к горизонтальной проекции С_НД_Н оси вращения.

Чтобы выполнить такой поворот точки А на чертеже, (Рис 4.13б), необходимо соблюдать следующие требования:

1.Провести через точку А_Н прямую (след S_Н плоскости вращения), перпендикулярную к С_НD_Н оси вращения, их пересечение определяет положение центра вращения О точки А и, следовательно, проекции радиуса вращения О_НА_Н и О_VA_V.

2.Определить одним их известных способов натуральную величину радиуса R_A (О_НА_О). (На рис. 4.13б применен способ построения прямоугольного треугольника О_НА_НА_О).

A) б)

Рис.4.13 Определение расстояния от точки А до линии СD способом вращения вокруг линии уровня

3.Отложить от центра О_Н на прямой, перпендикулярной к С_НD_Н, отрезок О_НА_О, равный натуральной величине радиуса R_A.

Задача: Определить натуральную величину треугольника АВС способом вращения вокруг горизонтали (Рис. 14).

Решение. Если за ось вращения построить горизонталь, принадлежащую плоскости треугольника АВС, то для поворота этой фигуры в положение, параллельное горизонтальной плоскости проекций, достаточно повернуть всего одну точку треугольника, не лежащую на оси вращения, а именно точку В. Остальные точки строятся из условия принадлежности их плоскости фигуры. Горизонталь А1 проведена через вершину А треугольника до пересечения с продолжением стороны ВС в точке 1. В треугольнике АВ1 вершины А и 1 лежат на оси вращения и не изменят своего положения при вращении вокруг горизонтали. Вращая точку В способом, рассмотренным на рис.4.13б, определяют положение ее новой проекции В¹. Соединив ее с точками А и 1, получим треугольник АВ’1, повернутый в положение, параллельное плоскости Н. Положение проекции точки С’, вершины С находят, проведя через точку С прямую перпендикулярную к оси вращения А1 до пересечения со стороной В1, поскольку все точки треугольника при его повороте перемещаются в параллельных плоскостях. Проекция А_НВ’_НС’_Н треугольника АВС определяет его натуральную величину, т.к. А_VВ’_VС’_V параллельна Н.

Date: 2015-07-01; view: 884; Нарушение авторских прав