Глава 5. МНОГОГРАННИКИ

Общие положения

Многогранником называют геометрическое тело, ограниченное плоскими многоугольниками. Эти многоугольники называют гранями общие стороны смежных многоугольников – ребрами, вершины многогранных углов, образованных его гранями, сходящимися в одной точке - вершинами многогранника.

Совокупность вершин и соединяющих их ребер называют сеткой многогранника.

Рассмотрим только выпуклые многогранники, то есть такие, все грани которых лежат по одну сторону от каждой его грани.

Из всех многогранников наибольший практический интерес представляют призмы, пирамиды и правильные многогранники.

Многогранник, две грани которого n–угольники, лежащие в параллельных плоскостях, а остальные грани параллелограммы, называется n–угольной призмой.

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой призмой.

Если боковые ребра призмы не перпендикулярны плоскостям оснований, то она называется наклонной призмой.

Многогранник, одна из граней которого произвольный многоугольник, а остальные грани треугольники имеющие общую вершину, называется пирамидой (рис.5.1б).

Если основание пирамиды правильный многоугольник и вершина пирамиды лежит на перпендикуляре восстановленном из центра этого многоугольника, то она называется правильной пирамидой (рис.5.1б).

К правильным многогранникам относятся те, грани которых представляют собой равные и правильные многоугольники, например: гексаэдр (куб) – правильный шестигранник (рис.5.1а), тетраэдр – правильная треугольная пирамида (рис.5.1в), октаэдр – правильный восьмигранник, додекаэдр – правильный двенадцатигранник, икосаэдр – правильный двадцатигранник.

Правильный четырехгранник, или тетраэдр (рис.5.1в), состоит из четырех равносторонних и равных треугольников. Они соединены по три около каждой вершины. Тетраэдр представляет собой частный случай пирамиды. Правильный шестигранник (куб), или гексаэдр, состоит из шести равных квадратов, соединенных по три у каждой вершины.

На комплексном чертеже построение многогранников сводится к построению его сетки (проекций его вершин и ребер). Из многогранников наибольший практический интерес представляют призмы, пирамиды и правильные многогранники.

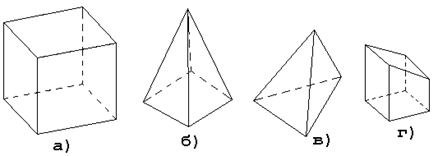
Рис. 5.1 – Многогранники: а) куб; б) пирамида; в) тетраэдр;

Date: 2015-07-01; view: 765; Нарушение авторских прав