Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать неотразимый комплимент Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?

Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Примечание. 1 Понять этические вопросы, иногда встающие перед исследователями, вам поможет кн.: Beanchamp T.L

⇐ ПредыдущаяСтр 128 из 130Следующая ⇒

1 Понять этические вопросы, иногда встающие перед исследователями, вам поможет кн.: Beanchamp T.L. et al., eds. Ethical Issues in Social Science Research. – Baltimore: Johns Hopkinks University Press.

 


Таблица А.1

ТАБЛИЦА СЛУЧАЙНЫХ ЧИСЕЛ

10097 37542 08422 99019 12807 32533 04805 68953 02529 99970   76520 64894 19645 09376 80157 13586 74296 09303 70715 36147   34673 24805 23209 38311 64032 54876 24037 02560 31165 36653   80959 20636 15953 88676 98951 09117 10402 34764 74397 16877   39292 00822 35080 04436 12171 74945 91665 33606 27659 76833
66065 31060 85269 63573 73796 74717 10805 77602 32135 45753   34072 45571 02051 05325 03529 76850 82406 65692 47048 64778   36697 35303 68665 90553 35808 36170 42614 74818 57548 34282   65813 86799 73053 28468 60935 39885 07439 85247 28709 20344   11199 23403 18623 83491 35273 29170 09732 88579 25624 88435
98520 11805 83452 88685 99594 17767 05431 99634 40200 67348   14905 39808 06288 86507 87517 68607 27732 98083 58401 64969   22109 50725 13746 36766 91826 40558 68248 70078 67951 08928   60970 29405 18475 90364 93785 93433 24201 40610 76493 61368   50500 52775 68711 29609 23478 73998 67851 77817 11062 34113
                        [c.514]
65481 80124 74350 69916 09893 17674 35635 99817 26803 20505   17468 17727 77402 66252 14225 50950 08015 77214 29148 68514   58047 45318 43236 36936 46427 76974 22374 00210 87203 56788   73039 21115 45521 76621 96297 57186 78253 64237 13990 78822   40218 14385 96286 94400 54382 16544 53763 02655 56418 14598
91499 80336 44104 12550 63606 14523 94598 81949 73742 49329   68479 26940 85157 11100 16505 27686 36858 47954 02040 34484   46162 70297 32979 12860 40219 83554 34135 26575 74697 52563   94750 53140 57600 96644 43651 89923 33340 40881 89439 77082   37089 42050 22222 28707 07207 20048 82341 06413 25815 31790
61196 15474 94557 42481 23523 90446 45266 28573 16213 78317   26457 95270 67897 97344 73208 47774 79953 54387 08721 89837   51924 59367 54622 16868 68935 33729 83848 44431 48767 91416   65394 82396 91190 03071 26252 59593 10118 42592 12059 29663   42582 33211 92927 25701 05522 60527 59466 45973 46670 82562
04493 00549 35963 59808 46058 52494 97654 15307 08391 85236   75246 64051 26898 45427 01390 33824 88159 09354 26842 92286   45862 96119 33351 83609 77281 51025 63896 35462 49700 44077   61962 54692 77974 13021 93910 79335 82391 50024 24892 83647   65337 23287 90103 78565 70617 12472 29529 39333 20106 42941
                        [c.515]
32179 69234 19565 45155 94664 00597 61406 41430 14938 31994   87379 20117 01758 19476 36168 25241 45204 75379 07246 10851   05567 15956 40419 43667 34888 07007 60000 21585 94543 81553   86743 18743 66674 59047 01540 17157 92423 36806 90033 35456   85394 97118 84962 20826 05014 11838 96338 85207 69541 51176
98086 33185 80951 79752 18633 24826 16232 00406 49140 32537   45240 41941 96382 71961 98145 28404 50949 70774 28296 06571   44999 89435 20151 69861 31010 08896 48581 23387 02591 24674   39094 88695 25016 74852 05455 73407 41994 25298 20539 61427   35441 37548 94624 00387 77938 31880 73043 61171 59579 91936
74029 54178 11664 48324 69074 43902 45611 49883 77928 94138   77557 80993 52079 31249 87637 32270 37143 84827 64710 91976   97790 05335 59381 02295 35584 17119 12969 71539 36870 04401   52527 56127 09973 32307 10518 58021 19255 33440 57546 21615   80814 36040 88461 15020 01848 51748 90324 23356 09994 76938

 

Таблица А.2

Размер выборки для определения уровней точности
(в процентах с доверительным интервалом в 95%, р=0,5)

Размер совокупности Размер выборки для следующих уровней точности
± 1% ± 2% ± 3% ± 4% ± 5% ± 10%
+ + +  
1 000 + + +
1 500 + +
2 000 + +
2 500 + 1 250
3 000 + 1 364
3 500 + 1 458
4 000 + 1 538
4 500 + 1 607
5 000 + 1 667
6 000 + 1 765
7 000 + 1 842
8 000 + 1 905
9 000 + 1 957
10 000 5 000 2 000 1 000
15 000 6 000 2 143 1 034
20 000 6 667 2 222 1 053
25 000 7 143 2 273 1 064
50 000 8 333 2 381 1 087
100 000 9 091 2 439 1 099
→ ∞ 10 000 2 500 1 111

* Доля в выборке единиц, обладающих измеренными характеристиками; для других значений р необходимый размер выборки будет меньше.

+ В этих случаях более 50% объема выборки дадут большую точность, чем требуемая. Поскольку нормальное распределение – это лишь грубое приближение к гипергеометрическому распределению, где п составляет более 50% oт N, формула, используемая при этих подсчетах, не применяется.

Источник: Таrо Y. Elementary Sampling Theory. – Englewood Cliffs, NJ.: Prentice-Hall, 1967. Р.398.

 


Таблица А.3

Размер выборки для определения уровней точности
(в процентах с доверительным интервалом в 99,7 %, р=0,5)*

Размер совокупности Размер выборки для следующих уровней точности
± 1% ± 2% ± 3% ± 4% ± 5%
+ + + + +
1 000 + + + +
1 500 + + +
2 000 + + +
2 500 + + +
3 000 + +
3 500 + +
4 000 + +
4 500 + +
5 000 + +
6 000 +
7 000 +
8 000 +
9 000 +
10 000 +
15 000 +
20 000 +
25 000
50 000
100 000
→ ∞

* Доля в выборке единиц, обладающих измеренными характеристиками; для других значений р необходимый размер выборки будет меньше.

+ В этих случаях более 50% объема выборки дадут большую точность, чем требуемая. Поскольку нормальное распределение – это лишь грубое приближение к гипергеометрическому распределению, где п составляет более 50% oт N, формула, используемая при этих подсчетах, не применяется.

Источник: Таrо Y. Elementary Sampling Theory. – Englewood Cliffs, NJ.: Prentice-Hall, 1967. Р.399.


Таблица А.4

РАСПРЕЛЕЛЕНИЕ χ2

df 0,05 0,01 0,001 df 0,05 0,01 0,001
1 2 3 4 5 3,841 5,991 7,815 9,488 11,070 6,635 9,210 11,345 13,277 15,086 10,827 13,815 16,266 18,467 20,515 26 27 28 29 30 38,885 41,337 40,113 42,557 43,773 45,642 48,278 46,963 49,588 50,892 54,052 56,893 55,476 58,302 59,703
6 7 8 9 10 12,592 14,067 15,507 16,919 18,307 16,812 18,475 20,090 21,666 23,209 22,457 24,322 26,125 27,877 29,588 32 34 36 38 40 46,194 48,602 50,999 53,384 55,759 53,486 56,061 58,619 61,162 63,691 62,487 65,247 67,985 70,703 73,402
11 12 13 14 15 19,675 21,026 22,362 23,685 24,996 24,725 26,217 27,688 29,141 30,578 31,264 32,909 34,528 36,123 37,697 42 44 46 48 50 58,124 60,481 62,830 65,171 67,505 66,206 68,710 71,201 73,683 76,154 76,084 78,750 81,400 84,037 86,661
16 17 18 19 20 26,296 27,587 28,869 30,144 31,410 32,000 33,409 34,805 36,191 37,566 39,252 40,790 42,312 43,820 45,315 52 54 56 58 60 69,832 72,153 74,468 76,778 79,082 78,616 81,069 83,513 85,950 88,379 89,272 91,872 94,461 97,039 99,607
21 22 23 24 25 32,671 33,924 35,172 36,415 37,652 38,932 40,289 41,638 42,980 44,314 46,797 48,268 49,728 51,179 52,620 62 64 66 68 70 81,381 83,675 85,965 88,250 90,531 90,802 93,217 95,626 98,028 100,425 102,166 104,716 107,258 109,791 112,317

Примечание. Для нечетных значений п между 30 и 70 можно взять среднее геометрическое табличных значений для df – 1 и df + l. Для больших значений п можно использовать выражение 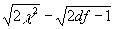как нормальное отклонение с единичным колебанием, принимая во внимание, что вероятность χ2 соответствует вероятности одного из концов нормальной кривой.

Источник:Fisher R.A., Yates F. Statistical Tables for Biological, Agricultural and Medical Research, 6th ed., published by Longman Group, Ltd., London (previously published by Oliver and Boyd, Edinburgh), Table IV.


Таблица А.5

⇐ Предыдущая121122123124125126127128129130Следующая ⇒





Date: 2015-06-11; view: 132; Нарушение авторских прав
mydocx.ru - 2015-2019 year. (0.008 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию