Признаки подобия треугольников

Первый признак подобия треугольников.
Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.

Второй признак подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Третий признак подобия треугольников.
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то такие треугольники подобны.

Доказательство (1-ый):
Рассмотрим два треугольника ABC и A₁B₁C₁.
Равны углы при вершинах A и A₁, кроме того,
=
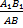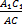
Отложим на луче AB отрезок AB₂ = A₁B₁ и проведем через B₂ прямую, параллельную BC. Получившийся треугольник AB₂C₂ подобен треугольнику ABC по основной теореме о подобных треугольниках.
Нам остается доказать, то треугольник AB₂C₂ равен треугольнику A₁B₁C₁.
В треугольниках A₁B₁C₁ и AB₂C₂ равны углы при вершинах A и A₁, A₁B₁ = AB₂. Кроме того, по условию
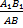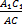= , а из того, что треугольники AB₂C₂ и ABC подобны, следует равенство = .
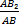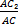Из этих двух равенств получаем (так как A₁B₁ = AB₂), то A₁C₁ = AC₂. Значит, треугольники A₁B₁C₁ и AB₂C₂ равны по первому признаку равенства треугольников.
Теорема доказана.

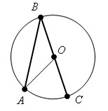
23. Теорема о вписанном угле.
Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Доказательство:
Пусть есть окружность с центром в точке O и угол ABC, вписанный в эту окружность, так что одна из сторон угла проходит через центр окружности.

Соединим точку A с центром окружности точкой O.
Δ ABO равнобедренный (BO=AO как радиусы). Следовательно, ∠OBA = ∠OAB.
Внешний угол при вершине O, угол AOC равен сумме углов OBA и OAB.
Значит ∠COA = ∠OBA.
В общем случае может быть два варианта, когда стороны угла не проходят через центр окружности. Проведем вспомогательный диаметр BD:

Вариант 1:
Тогда ∠ABC = ∠ABO + ∠CBO = ∠AOD + ∠COD = ∠AOC
Вариант 2:
Тогда ∠ABC = ∠CBD - ∠ABD = ∠COD - ∠AOD = ∠AOC
Теорема доказана.

Следствия из теоремы:
1. Если вписанные углы опираются на одну дугу, то они равны.
2. Вписанный угол в окружность опирается на диаметр тогда и только тогда, когда он прямой.

24. Вывод формул площади треугольника.
1. Через высоту и основание:
Достроив треугольник ABC до параллелограмма ABDC, получим
S_ABDC = a*h_a = 2S => S = ah_a

2. Через две стороны и угол между ними:
Поскольку h_a = b*sin C, то справедлива формула: S = ab*sin C
3. Через полупериметр и радиус вписанной окружности.
Соединив центр O вписанной окружности с вершинами треугольника, получим
S = S_ΔAOB + S_ΔBOC + S_ΔAOC = cr + ar + br = (a+b+c)r

25. Декартова система координат.
Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O, причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки.

Вывод формулы расстояния между двумя точками.
Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x – x₀;

BC = y – y₀.
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = .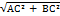
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Уравнение окружности.
(x - x₀)² + (y – y₀)² = r², где
x₀, y₀ – координаты центра окружности.
r – радиус окружности.

Взаимное расположение окружностей.
1. Одна окружность лежит внутри другой.
2. Одна окружность касается другой изнутри.
3. Окружности пересекаются.
4. Одна окружность касается другой снаружи.
5. Одна окружность лежит вне другой.

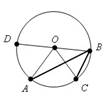
26. Теорема о произведении отрезков пересекающихся хорд окружности.
При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.

Доказательство:
угол BAD = углу BCD = 1/2 BmD (вписанные углы опираются на одну дугу)
=> треугольник APD подобен треугольнику CPD (по двум углам)
=> PD/PB = AP/CP.
Теорема доказана.

27. Теорема о произведении отрезков секущей и квадрате касательной.
Квадрат касательной равен произведению секущей на её внешнюю часть.

Доказательство:
Проведём отрезки АК и ВК. Треугольники АКМ и ВКМ подобны: угол М у них общий, а углы АКМ и В равны, так как каждый из них измеряется половиной дуги АК.
Следовательно, MK/MA = MB/MK, или MK² = MA*MB.
Теорема доказана.

28. Свойство площадей подобных треугольников.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Доказательство:
Пусть треугольники ABC и А1В1С1 подобны, причем коэффициент подобия равен k O, обозначим буквами S и S1 площади этих треугольников. Так как A=A1, то

S/S1 = AB*AC/A1B1*A1C1 (по теореме об отношении площадей треугольника).

По формулам имеем: АВ/А1В1 = k, AC/A1C1 = k, поэтому S/S1 = k2

Теорема доказана.

29. Теорема о точке пересечения медиан треугольника.
Медианы треугольника пересекаются в одной точке и делятся этой токой в отношении 2: 1, считая от вершин треугольника.

Доказательство:
Медиана AA₁ треугольника ABC представляет собой геометрическое место точек M внутри треугольника, для которых треугольники ABM и ACM равновелики.
В самом деле, так как треугольники BAA₁ и CAA₁ равновелики, то равны и их высоты к общей стороне AA₁.
Потому для любой точки M на AA₁ также будут равны высоты к AM в треугольниках BAM и CAM, а значит, эти треугольники для всех M равновелики. Точно так же проводится и обратное рассуждение. Если тока M внутри треугольника ABC такова, что треугольники ABM и ACM равновелики, то равны и высоты этих треугольников к общей стороне AM.

Пусть AM пересекает BC в точке A1. Треугольники BAA1 и CAA1 равновелики, поскольку у них AA1 общая сторона, и высоты, опущенные на нее, равны. И из равенства площадей треугольников BAA1 и CAA1 следует, что A1 ¾ середина BC, т. е. точка A1 совпадает с A1.
Теорема доказана.
Треугольники, полученные при пересечении всех медиан треугольника, равновелики.