Признак вписанного четырёхугольника

Если в четырёхугольнике сумма противолежащих углов равна 180°,то около него можно описать окружность.

Доказательство:
Пусть ABCD - такой четырёхугольник, что ∠A+∠C = 180°. Проведём окружность через три вершины A, B и D четырёхугольника. В таком случае, вершина C может оказаться как внутри окружности, так и снаружи.
Рассмотрим второй случай. По теореме об угле между двумя секущими:
∠C = => ∠C <
Так как по теореме о вписанном угле ∠A = 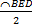, то ∠A + ∠C < 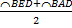= 180°,
то есть ∠A+∠C < 180°, что противоречит условию.
Теорема доказана.

21. Признак описанного четырёхугольника.
Если в выпуклом четырехугольнике суммы противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

Доказательство:
Воспользуемся методом от противного. Пусть для четырехугольника ABCD выполняется условие AB + CD = BC + DA. Проведем биссектрисы угловA и B и обозначим через O точку их пересечения. Точка O равноудалена от сторон AD и AB, а также от сторон BA и BC. Значит, точка O равноудалена от трех сторон AB, AD и BC, поэтому мы можем построить окружность с центром в O, касающуюся этих трех сторон четырехугольника ABCD. Пусть эта окружность не касается стороны CD. Для определенности можно считать, что она не пересекает стороны CD. Проведем через C прямую, касающуюся этой окружности, и обозначим через D1 ее точку пересечения с AD. Имеем два четырехугольника ABCD и ABCD1, в каждом из которых суммы противоположных сторон равны. В первом - по условию теоремы, во втором потому, что он описанный. Запишем оба эти равенства:
AB + CD = BC + AD, AB + CD₁ = BC + AD₁.
Вычтем второе равенство из первого. Получим: CD - CD₁= DD₁ или CD = CD₁ + DD₁. Последнее равенство означает, что точки C, D и D₁ лежат на одной прямой, так как в противном случае оно противоречило бы неравенству треугольника. Значит, точки D и D₁ совпадают, и четырехугольник ABCD является описанным.
Теорема доказана.