Подготовка к зачёту по геометрии в 9 классе

1. Признаки равенства треугольника.
1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Доказательство первого признака:
Рассмотрим два треугольника ABC и A₁B₁C₁.
Пусть в этих треугольниках равны стороны AB и A₁B₁, BC и B₁C₁, а угол ABC равен углу A₁B₁C₁.
Тогда треугольник A₁B₁C₁ можно наложить на треугольник ABC так, чтобы угол A₁B₁C₁ совпал с углом ABC.
При этом можно расположить треугольник A₁B₁C₁ так, чтобы сторона А₁В₁ совпала со стороной АВ, а сторона B₁С₁ - со стороной ВС. Тогда треугольники совпадут полностью, поскольку совпадут все их вершины.
Теорема доказана.

2. Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.

Доказывать через теорему о площади треугольника через синус угла.

Обобщённая теорема синусов.
Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.

Формула площади треугольника через три стороны и R.
S =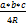

3. Признаки равнобедренного треугольника.
1. Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
2. Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным.
3. Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным.
4. Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным.
5. Если в треугольнике две стороны равны, он равнобедренный.

Свойства равнобедренного треугольника.
1.Если треугольник является равнобедренным треугольником, то углы при его основании равны.
2. В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.

Свойство медианы равнобедренного треугольника.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Доказательство:
Пусть ABC – равнобедренный треугольник, а CD медиана, проведенная к основанию AB этого треугольника.
Треугольники ACD и BCD равны по первому признаку равенства треугольников: AC=AB – так как ABC равнобедренный, AD=DB – так как CD медиана и разбивает основание AB пополам, ∠ CAD = ∠ CBD – так как ABC равнобедренный.
Из равенства треугольников следует:

1) так как ∠ ACD = ∠ BCD, то CD – биссектриса;

2) так как ∠ CDA = ∠ CDB и эти углы смежные, то они по 90° и CD – высота.

Теорема доказана.

4. Основные свойства площадей.
1. Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не изменится.
2. Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований.
3. Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.
4. Отношение площадей подобных треугольников равны квадрату коэффициента подобия.
5. Медианы треугольника делят его на шесть равновеликих частей.

5. Теорема о серединном перпендикуляре к отрезку.
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Доказательство:
Обозначим буквой M произвольную точку серединного перпендикуляра a к отрезку AB и докажем, что AM = BM.
Если точка M совпадает с серединой O отрезка AB, то справедливость равенства AM = BM очевидна. Если же M и O – различные точки, то прямоугольные треугольники OAM и OBM равны по двум катетам, поэтому AM = BM. Теорема доказана.

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его сторонам.

6. Понятие о движении.
Движение – это отображение пространства на себя, сохраняющее расстояния между точками.

Общие свойства движений.
1. При движении три точки, лежащие на прямой, переходят в три точки, лежащие на прямой, причем точка, лежащая между двумя другими, переходит в точку, лежащую между образами двух других точек.
2. Образом отрезка при движении является отрезок.
3. Образом прямой при движении является прямая, а образом луча - луч.
4. При движении образом треугольника является равный ему треугольник, образом плоскости - плоскость, причем параллельные плоскости отображаются на параллельные плоскости.
5. При движении углы сохраняются, т.е. всякий угол отображается на угол того же вида и той же величины.

Центральная, осевая симметрия – симметрия относительно точки, прямой.

Доказательство того, что осевая симметрия является движением.
Докажем, что осевая симметрия является движением, используя метод координат. Примем прямую А за ось Х декартовых координат.
Тогда при симметрии относительно нее точка, имеющая координаты (x;y) будет преобразована в точку с координатами (x, -y).
Возьмем любые две точки A(x₁, y₁) и B(x₂, y₂) и рассмотрим симметричные им относительно оси Х точки A'(x₁,- y₁) и B'(x₂, -y₂). Вычисляя расстояния A'B' и AB, получим:
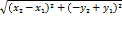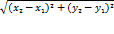A’B’ = + = AB
Таким образом, осевая симметрия сохраняет расстояние, следовательно, она является движением.

7. Теорема о биссектрисе угла.
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Доказательство:
Обозначим буквой M произвольную точку биссектрисы неразвернутого угла A, проведем перпендикуляры MH и MK.
Прямоугольные треугольники AMH и AMK равны по гипотенузе и острому углу (AM – общая гипотенуза, ∠1 = ∠2 по условию). Следовательно, MH = MK.
Теорема доказана.

Обратная теорема о биссектрисе угла.
Каждая точка, лежащая внутри неразвернутого угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Доказательство:
Рассмотрим точку M, которая лежит внутри неразвернутого угла A и равноудалена от его сторон, т. е. перпендикуляры MH и MK к сторонам равны. Докажем, что луч AM – биссектриса угла A.
Прямоугольные треугольники AMH и AMK равны по гипотенузе и катету (AM – общая гипотенуза, MH = MK по условию). Поэтому, ∠1 = ∠2, т. е. луч AM – биссектриса угла A.
Теорема доказана.

Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис его внутренних углов.

8. Теорема Пифагора.
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.
Доказывать через построение до квадрата.

Обратная теорема Пифагора.
Если в треугольнике со сторонами a, b и c выполняется равенство c2 = a 2 + b 2, то этот треугольник прямоугольный, причем прямой угол противолежит стороне c.

Доказательство:
Рассмотрим треугольник, стороны которого равны a и b, а угол между ними - прямой. По теореме Пифагора квадрат третьей стороны равен a2 + b2, т. е. эта сторона равна c. Значит, построенный нами треугольник равен данному по третьему признаку равенства треугольников.

9. Признаки параллельности прямых.
1. Если две прямые перпендекулярны третей, то они параллельны

2. Если накрест лежащие углы равны, то прямые параллельны.
3. Если соответственные углы равны, то прямые параллельны.
4. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.

Доказательство:
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.

10. Вектор.
Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Векторы называются равными, если они сонаправлены и их длины равны.
Сумма A + B будет вектор, начало которого совпадает с началом вектора А, а конец – с концом вектора В.
Разность А - В будет вектор, конец которого совпадает с началом вектора А, а начало – с концом вектора В.
Два коллинеарных вектора А и В называются сонаправленными, если их направления совпадают.
Два коллинеарных вектора А и В называются противоположно направленными, если их направления противоположны.
Абсолютная величина вектора – модуль его длины.

11. Окружность.
Окружность – множество точек, равноудалённых от данной.

Теорема о хордах, стягивающих равные дуги.
Равные дуги стягиваются равными хордами.

Доказательство:
Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК.
Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.

Теорема о диаметре, перпендикулярном хорде.
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.

Доказательство:
Пусть диаметр АВ перпендикулярен к хорде CD. Требуется доказать, что ⌒СЕ = ⌒ЕD, ⌒CB = ⌒ВD, ⌒СА = ⌒DА.
Соединим точки C и D с центром окружности О. В равнобедренном треугольнике

СОD отрезок ЕО является высотой, проведённой из вершины O на основание СD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и ∠1 = ∠ 2. Но ∠1 и ∠2 – центральные углы. Отсюда равны и соответствующие им дуги, а именно

⌒СВ = ⌒ВD. Дуги ⌒СА и ⌒ВА также равны между собой, как дополняющие равные дуги до полуокружности.

Теорема доказана.

Теорема о хордах, равноудалённых от центра окружности.
Если хорды равноудалены от центра окружности, то они равны.

12. Произведение вектора и числа.
Произведение ненулевого вектора на число - это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Необходимым и достаточным условие коллинеарности двух векторов является равенство нулю их векторного произведения.