
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приближение узкого резонанса для профи 311
|
|
Поэтому когда мы в дальнейшем будем пользоваться понятием потока замедляющихся нейтронов Ф(U), мы должны всегда помнить, что это не интегральный поток по всей области летаргии, а это поток нейтронов при летаргии U, нормированный на единичный интеграл летаргии, т.е. в интервале летаргии 1. Потому что для замедляющихся нейтронов, чем больше интервал, тем больше там будет нейтронов. Возьмите полный интеграл – там будет полное количество нейтронов. Но нам для изучения резонансного поглощения нейтронов, полное количество нейтронов не нужно, бесполезно. Поэтому Ф(U) – это поток нейтронов, нормированный на единичный интервал летаргии.
И вот теперь, мы уже можем более строго ввести в рассмотрение непосредственно нужную нам величину, характеризующую замедление нейтронов в реакторе, которая называется плотность замедления нейтронов q (3.12a). Эта плотность замедления нейтронов зависит от летаргии и численно равна потоку нейтронов при летаргии U, нормированному на единичный интервал летаргии, умноженному на макроскопическую замедляющую способность
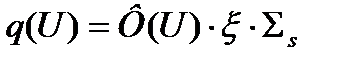 . (3.22)
. (3.22)
Другое название этой величины, может быть, более понятное для восприятия – поток нейтронов по энергетической оси.
Как определить этот поток нейтронов по энергетической оси физически? Можно определить это следующим образом. Поток нейтронов по энергетической оси равен количеству нейтронов в 1 см3, попадающих или пересекающих ось летаргии U в 1 с. Вернее, не ось, а уровень, т.е. поток нейтронов по энергетической оси равен количеству нейтронов в 1 см3, попадающих в 1 с из области летаргии, меньше U в область летаргии, больше U. Ну, а по энергии это будет наоборот – попадающих из области энергий больше Е в область энергий, меньше Е. Вот это поток нейтронов по энергетической оси, как бы скорость замедления нейтронов, с которой они спускаются вниз по энергии.
Вот где-то там наверху родились нейтроны, а дальше что с ними происходит – какой их будет поток по энергетической оси? От чего он зависит? Во-первых, он зависит от потока нейтронов при данной летаргии Ф(U). Далее, он зависит от того, сколько упругих столкновений произойдет в 1 см3 в 1 с. Чтобы это найти, мы этот поток нейтронов умножаем на макроскопическое сечение рассеяния Ss – тогда мы получаем число упругих столкновений в 1 с в 1 см3. А дальше надо умножить на x - это мы получим количество нейтронов, которые в 1 сбудут пересекать вот этот уровень летаргии U и замедляться.
В области U = 18,2 есть всплеск потому, что там происходит накопление тепловых нейтронов, т.е. в области выше тепловой нейтроны все пока замедляются, они не задерживаются в этой области, замедляются и замедляются,а дальше в области тепловых энергий замедление нейтронов прекращается, из-за того, что кинетическая энергия атомов замедлителя сравнивается с кинетической энергией нейтронов. Вот если бы мы представили себе идеальный замедлитель, в котором сечение поглощения точно было бы равно нулю, тогда тепловые нейтроны никуда бы не девались. Т.е. была бы такая картина: где-то вверху действует источник быстрых нейтронов, от этого источника быстрых нейтронов появляется поток нейтронов по энергетической оси, все они замедляются. И вот в отсутствие поглощения количество тепловых нейтронов растет, растет и растет. Но так быть не может. На самом деле наступает баланс – количество нейтронов, которое в 1 с попадает в тепловую область должно в стационарном случае равняться количеству поглощенных тепловых нейтронов. Потому что если мы рассматриваем стационарно работающий реактор, все его параметры должны быть неизменны во времени.
А вот поток нейтронов будет зависеть от сечения, он может быть разный – большой или маленький, в зависимости от того, какое макроскопическое сечение поглощения тепловых нейтронов. Если маленькое сечение, то этот всплеск будет большой. Например, в «нейтронной ловушке» или отражателе реактора (особенно в графитовом) маленькое сечение поглощения, поэтому там всегда большой поток тепловых нейтронов по сравнению с потоком в активной зоне. Вот почему в тепловой области и есть такой всплеск.
Теперь, зная эти понятия, мы можем приступить к рассмотрению уже резонансного поглощения нейтронов, вернее к нахождению вероятности избежать резонансный захват на 238Uв процессе замедления.
Для того чтобы нам легче было дальше рассуждать, мы выделим и рассмотрим сначала один резонанс (мы знаем по графикам, что там резонансов этих сотни, и на каждом из этих резонансов по чуть-чуть идет поглощение). На рис. 3.8 изображен один резонанс в масштабе летаргии U, т.е. сечение захвата s 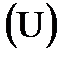 , допустим, на каком-то нулевом резонансе
, допустим, на каком-то нулевом резонансе 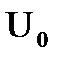 (конечно, на резонансе сечения захвата 238U
(конечно, на резонансе сечения захвата 238U 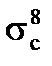 ).
).
В начале координат ноль, значит, замедление идет в сторону возрастания летаргии.
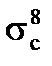
|
| smax |
| 0 |
| U0 |
| U |
| Рис. 3.8а Сечение одного резонанса 238U |
| Замедление |
Нам будет проще вести наши рассуждения, если мы вначале будем искать не вероятность избежать резонансного захвата на этом резонансе, а будем, наоборот, искать сопряженную функцию - вероятность захвата. Но ясно, что вероятности этих двух событий в сумме дают единицу. Нейтрон может или захватиться или избежать захвата. Что-то одно всегда происходит, поэтому сумма этих вероятностей на одном резонансе обязательно равна единице. Таким образом, если мы найдем вероятность захвата, то потом, если мы вычтем эту вероятность захвата из единицы, мы найдем вероятность избежать захвата.
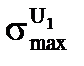
|
| sс |
| DU1 |
| U |
| U1 |
| Рис..3.8 в Модель резонанса «столбик» |
Давайте найдем вероятность захвата на одном резонансе, пусть это будет первый резонанс U1, который встречается на пути нейтронов в процессе замедления. Как мы определим вероятность поглощения?
В числителе мы должны записать количество нейтронов, которые поглощаются в 1 с в 1 см3 этим резонансом. В дальнейшем мы упростим наши вычисления вот каким образом – мы вместо вот такой действительной кривой 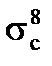 (рис. 3.8а) возьмем модель
(рис. 3.8а) возьмем модель 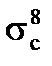 в виде столбика (рис. 3.8.в), но так, чтобы площади под кривыми были равны, в среднем это будет то же самое U1,. Т.е. мы аппроксимируем это сечение
в виде столбика (рис. 3.8.в), но так, чтобы площади под кривыми были равны, в среднем это будет то же самое U1,. Т.е. мы аппроксимируем это сечение 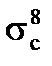 , т.е. мы будем считать, что вне этого интервала сечения равны нулю, а внутри интервала равны как раз максимуму
, т.е. мы будем считать, что вне этого интервала сечения равны нулю, а внутри интервала равны как раз максимуму 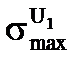 . А ширину столбика назовем шириной резонанса DU1.
. А ширину столбика назовем шириной резонанса DU1.
Число поглощенных нейтроновбудет равно потоку нейтронов Ф(U1), умноженному на ширину интервала DU1, потому что нейтроны поглощаются только в узком резонансе, и умноженному на макроскопическое сечение поглощения. Надо сразу сказать, что DU намного меньше единицы, т.е. резонанс - это очень узенький интервал. Вот это в точности есть число нейтронов, поглощенных в 1 с одним резонансом в 1 см3238U:
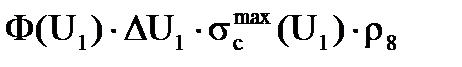 . (19.12)
. (19.12)
Это мы нашли числитель – количество поглотившихся нейтронов.А чтобы найти вероятность поглощения, в знаменателе надо записать, сколько нейтронов подходит к этому резонансу из области замедления – это как раз и есть плотность замедления q, т.е. в знаменателе мы должны записать q(U1). Вот эту линию U1 пересекает в 1 с в 1 см3 вот такое количество нейтронов, поток нейтронов по энергетической оси, плотность замедления. Т.е. можно записать
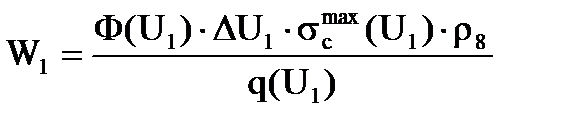 . (3.23)
. (3.23)
Если бы поглощения не было, то количество нейтронов, подошедших к уровню U1 было бы равно количеству тех нейтронов, которые из него вышли. А раз на резонансе какое-то количество нейтронов поглощается, то значит, после U1 нейтронов выйдет меньше.
В знаменатель формулы (3.23) необходимо подставить вот эту формулу для q(U1), но при этомпонимая, что вот этот поток нейтронов при наличии резонанса (обозначим с индексом r), не равен потоку нейтронов при этой летаргии U1 в случае, если бы резонанса не было. Потому что в том месте, где у нас есть резонанс, поток нейтронов будет уменьшаться.
Поэтому поток нейтронов в отсутствие резонанса просто обозначен Ф(U), без индекса, а поток в резонансе обозначен с индексом «r» Фr(U), т.е. эти потоки не равны, иначе они просто сократились бы.
Таким образом, можем записать, что вероятность поглощения нейтронов на первом резонансе будет равна
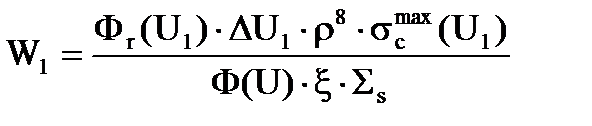 (3.24)
(3.24)
| Без учета резонанса |
Обычно x вообще зависит только от массы ядра замедлителя, а микроскопические сечения рассеяния от энергии (или от летаргии) практически не зависят, это почти постоянные величины. Вот захват, деление – сильно зависят от энергии, а рассеяние очень слабо. А вообще, на узком интервале, можно точно считать, что это постоянные величины.
Таким образом, в выражении (3.24) для W1 нам все величины известны. Микроскопическое сечение нам известно, без этого невозможно подсчитать вероятность избежать резонансного захвата, также мы должны знать ширину и высоту резонанса – это нам из таблиц известно, из экспериментальных данных. Макроскопическое сечение рассеяния Ss и x мы вычисляем, поскольку знаем, какой там замедлитель – водород, углерод и т.д. А вот отношение потоков нам неизвестно и, собственно, главная задача для расчета вероятности поглощения и состоит в том, что нам нужно найти отношение вот этих вот потоков нейтронов 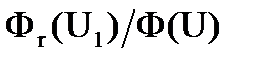 – потока с учетом влияния резонанса к потоку, когда резонанса нет.
– потока с учетом влияния резонанса к потоку, когда резонанса нет.
Чтобы найти это отношение, мы должны записать очень важное балансное соотношение, из которого мы и будем искать 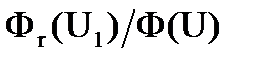 , потому что дальше пойдут только формальные преобразования. А вся физика будет заключаться вот в этом балансном соотношении. Какой же баланс мы должны записать?
, потому что дальше пойдут только формальные преобразования. А вся физика будет заключаться вот в этом балансном соотношении. Какой же баланс мы должны записать?
Поскольку в этот узкий энергетический интервал DU нейтроны попадают в результате упругих столкновений с левой стороны от процесса замедления, мы должны записать, сколько нейтронов попадет слева в этот интервал DU, т.е. из области выше данной, столько же в 1 суйдет из этого интервала DU. Потому что мы рассматриваем стационарный случай. Но уходить из этого интервала нейтроны будут уже двумя путями, т.е. если попадают они в DU только в результате упругого замедления из верхней области энергий, то выбывают они двумя путями – как в результате истинного поглощения нейтронов (исчез нейтрон, поглотился), так и в результате упругих столкновений с ядрами замедлителя внутри этого узкого интервала. И вот здесь мы как раз используем приближение узкого резонанса (мы с вами уже это писали), оно означает, чтоDЕ - потеря энергии при одном столкновении для всех замедлителей намного больше, чем ширина резонанса DU. Т.е. приближение узкого резонанса, которое всегда справедливо, можно записать так:
DU<<DЕ. (3.25)
Можно перейти к летаргии, разделить на Е и взять логарифм. Т.е. вот есть, например, ступенька замедления. Допустим, она равна какой-то величине, если взять водород, она вообще равна единице, это средняя потеря энергии, среднелогарифмическая. А если взять резонанс, то он в летаргических единицах составляет тысячные, даже, наверное, десятитысячные значения. Т.е. это приближение всегда верно. Поэтому, раз резонанс узкий, мы можем считать, что любое упругое столкновение нейтрона с ядрами замедлителя внутри этой энергетической полоски приведет к тому, что нейтрон выскочит из нее, исчезнет, т.е. это будет убыль нейтрона. Можно рассмотреть процесс упругого замедления вот здесь, допустим, где большая ступенька - часть нейтронов попадет сюда, часть туда, т.е. нейтроны равномерно будут рассеиваться, а вот вероятность того, что нейтрон здесь стукнулся и здесь же остался –будет ничтожная, потому что это должно быть настолько легкое касательное столкновение и настолько потеря энергии невелика, что можно пренебречь теми нейтронами, которые чуть-чуть скользнут по ядру замедлителя и почти не потеряют энергию. Таких нейтронов будет очень мало, потому что максимальная потеря энергии при одном столкновении намного больше, чем ширина резонанса. Вот это основное допущение узкого резонанса, из которого мы делаем вывод, что любое упругое столкновение нейтронов внутри резонанса приводит к тому, что нейтрон из этого резонанса выбывает. Т.е. если нейтрон получает другую энергию, значит, он потерян для этого баланса. Поэтому мы и говорим, что нейтроны в этот резонанс прибывают и отсюда, и отсюда, отовсюду – за счет процесса упругого столкновения. Т.е. в этот энергетический интервал нейтроны прибывают сверху из области больших энергий (или меньших летаргий), и мы говорим, что количество нейтронов, попавших в него, должно равняться количеству нейтронов, из него выбывших. Попадают они в интервал только одним путем – в результате упругих столкновений из более высоких областей энергий, а выбывают уже двумя путями – за счет истинного поглощения (нейтрон вообще исчез) или путем упругого замедления. Вот это соотношение мы должны сейчас записать и из него уже получать отношение потоков. Вот смысл этого баланса.
Формально запишем этот баланс. Сначала запишем, сколько нейтронов выбывает из этого интервала. Это понятно, сколько выбывает. А поглощается:
Фr(U1)×DU1×r8× 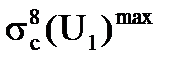 ,
,
это все нейтроны, которые поглотились в 1 с в 1 см3 – они же и выбыли из этого энергетического интервала. Теперь мы должны к ним добавить нейтроны, выбывшие в результате упругого рассеяния. Вот исходя из того, что резонанс узкий, мы должны записать здесь просто число упругих столкновений в этом интервале. Как мы его запишем? Так же, запишем поток нейтронов при U1 - Фr(U1)×DU1×Ss, т.е. мы считаем, что при любом упругом столкновении нейтрон вылетает, он как бы потерян для этой энергии, он приобрел другую энергию, вне этого интервала. Значит, эта часть ясна.
Теперь мы должны записать, а сколько же нейтронов попадает в этот интервал за счет замедления? Строго говоря, мы должны как бы интегрировать, т.е. брать количество нейтронов, которые попадут из разных областей в DU и т.д.
Но мы воспользуемся сейчас другим соотношением, очень простым. Представим себе, что у нас нет в замедлителе 238U, т.е. рассмотрим один замедлитель. Тогда у нас соотношение будет такое: сколько в эту область попало нейтронов в результате упругого столкновения, ровно столько же нейтронов и выйдет, тоже в результате упругого столкновения. И вот вместо того, чтобы заниматься интегрированием (сколько сюда попадет), мы запишем здесь, а сколько отсюда выходило бы нейтронов в 1 св результате упругих столкновений, если бы захвата не было, если бы 238U не было. Т.е. тогда мы здесь должны записать поток нейтронов, но уже без индекса r, а вот тот поток нейтронов, который характерен для этой области Ф(U1)×DU1×Ss. Тогда уравнение баланса будет выглядеть так
 . (3.26)
. (3.26)
Рассматриваем еще раз это уравнение баланса. С левой стороны написано количество нейтронов, выбывающих в 1 с в 1 см3из интервала летаргии шириной DU1 за счет двух процессов – истинного поглощения (слева, первый член - количество поглощенных нейтронов) и за счет упруго рассеянных нейтронов. Раз резонанс узкий, мы считаем, что при любом упругом рассеянии нейтрон уже из области резонанса выбывает. С правой стороны, строго говоря, у нас записано количество нейтронов, тоже выбывающих из такого же энергетического интервала или интервала летаргии DU1 путем упругого рассеяния, но в том случае, если бы резонанса не было, если бы вообще был бы один чистый замедлитель. Это по смыслу. Но ведь те нейтроны, которые попадают в этот интервал сверху, они не знают, есть здесь резонанс или нет. Поэтому мы с полным правом можем считать, что то количество нейтронов, которое выбывало бы из этого резонанса в отсутствие резонансного поглощения, оно равно количеству нейтронов, которое попадает в ширину этого интервала. А попадает одинаковое количество нейтронов, независимо от того, есть резонанс или нет резонанса, потому что резонанс назад не действует, он действует только в ту сторону. Если резонанс может поглотить, тогда поток нейтронов будет меньше.
А теперь мы можем заняться преобразованиями. Из соотношения (3.26) найдем нужное нам отношение потоков нейтронов 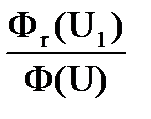 . Вынесем Фr за скобки, тогда получится
. Вынесем Фr за скобки, тогда получится
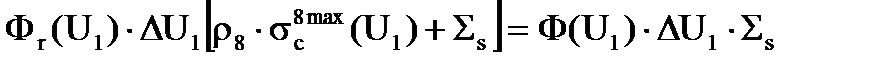 . (3.27)
. (3.27)
На DU1 можно сократить, тогда в явном виде можно записать отношение, которое нам нужно

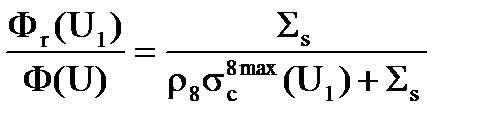 , (3.28)
, (3.28)
здесь 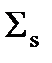 - постоянно, поэтому мы не пишем аргумент, от которого она бы зависела.
- постоянно, поэтому мы не пишем аргумент, от которого она бы зависела.
Теперь подставим в выражение (3.24) для W1 вот это отношение (3.28). Тогда получим
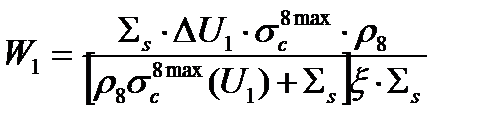 . (3.29)
. (3.29)
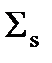 тоже можно сократить. В знаменателе вынесем за скобку
тоже можно сократить. В знаменателе вынесем за скобку 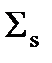 . Тогда будет следующее
. Тогда будет следующее
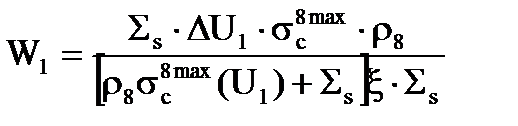 . (3.30)
. (3.30)
Вот какая величина получена для вероятности захвата в процессе замедления на первом резонансе.
Теперь найдем, наоборот, вероятность избежать захвата на первом резонансе j1. Для этого из единицы вычтем величину W1 (3.30)
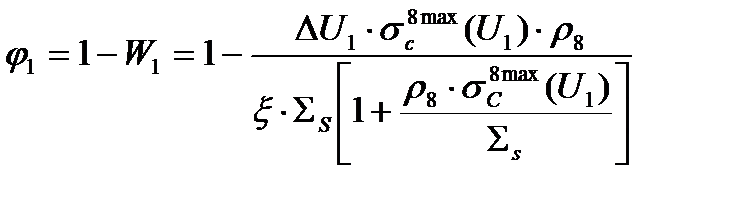 . (3.31)
. (3.31)
Прологарифмируем выражение (3.31), т.е. возьмем от этого выражения натуральный логарифм. Тогда
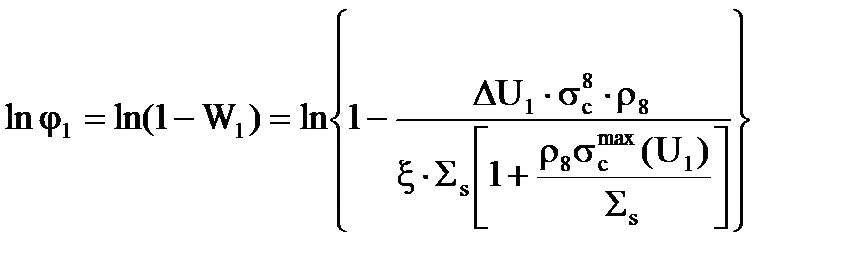 . (3.32)
. (3.32)
Мы нашли j1 как 1 – W1. Но на самом деле резонансов много, и если известна вероятность избежать захвата на одном резонансе, то можно найти вероятность избежать захвата на всем количестве резонансов.
Поскольку вероятности независимых событий в теории вероятности умножаются (как ив теории надежности), то.
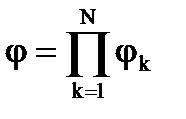 , (3.33)
, (3.33)
где N – полное количество резонансов.
Если j равно произведению jк, тоlnj это будет логарифм произведения, и чтобы найти вероятность избежать захвата на всех резонансах, надо просто перемножить вероятности избежать захвата на каждом резонансе. Дальше воспользуемся тем, что логарифм произведения равен сумме логарифмов. Поэтому можем записать, что:
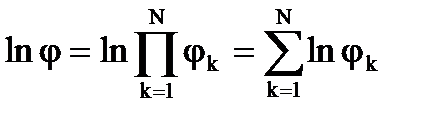 . (3.34)
. (3.34)
Подставив значения j, получим:
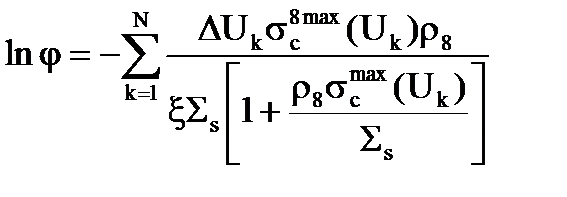 . (3.35)
. (3.35)
От суммы перейдем к интегралу, то верхняя граница будет UТ (тепловое), а интегрирование будет проводиться по всей области. Вместо Uк везде нужно просто текущее значение написать. Вместо DUк - просто dU – дифференциал. Тогда у нас будет
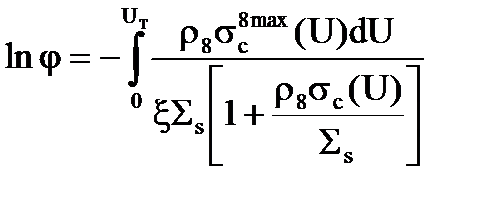 . (3.36)
. (3.36)
Далее мы делаем такое предположение (на самом деле очень близкое к действительности), что у нас сечение sс(U) в области резонансов большое, а в промежутках – ноль. Что нам важно здесь - чтобы сечение было правильное, а здесь оно все равно вне резонанса равно нулю и когда мы интегрируем, то если сечение равно нулю, тогда и поток нейтронов, хоть он там есть, но умноженный на нулевое сечение, в этот интеграл, в эту площадь никакой вклад не даст. Давайте дальше поработаем с выражением (3.36. Запишем снова lnj.
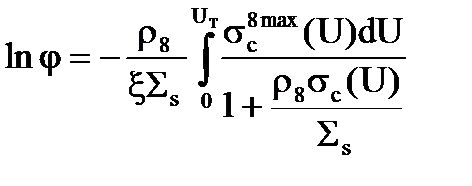 . (3.37)
. (3.37)
Интеграл, входящий в формулу (3.37) получил название эффективный резонансный интеграл поглощения. Мы его сейчас выпишем, а потом будем анализировать его подробно
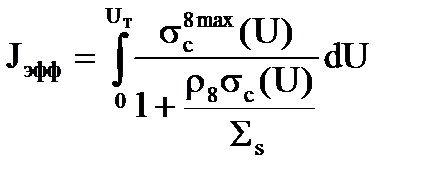 . (3.38)
. (3.38)
Если продолжить алгебраически запись, то тогда
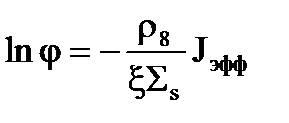 . (3.39)
. (3.39)
И последнее формальное преобразование - надо это выражение (3.39) пропотенцировать, т.е. от логарифма перейти к экспоненте. Поскольку натуральный логарифм имеет основание е, то тогда пропотенцированное выражение будет равно
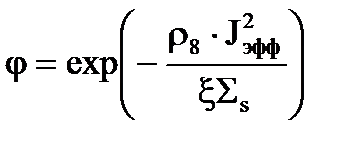 .(3.40)
.(3.40)
Вот мы получили формально выражение для вероятности избежать резонансного захвата в процессе замедления на 238U в гомогенном случае (мы рассматриваем гомогенный случай).
Давайте проанализируем немного выражение (3.40). Как влияет на j каждый из параметров, которые входят в показатель выражения? Ясно, что когда мы увеличиваем в числителе концентрацию ядер 238U, а показатель степени отрицательный, то само j будет уменьшаться. Это вроде бы физически понятно – чем больше ядер резонансного поглотителя, тем и поглощение должно быть больше, а вероятность избежать захвата, наоборот, меньше. Теперь эффективный резонансный интеграл поглощения. В теории резонансного поглощения для замедляющихся нейтронов резонансный интеграл играет такую же роль, как для тепловых нейтронов сечение захвата тепловых нейтронов. Т.е. если эффективный резонансный интеграл будет больше, то будет поглощаться больше нейтронов, а поскольку этот показатель здесь отрицательный, вероятность избежать захвата будет меньше.
Да, из формулы самим сечением 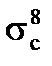 вырезаются те куски, где сечение отлично от нуля. Там, где сечение равно нулю все равно в интеграл вклада никакого не будет (если сечение равно нулю). Будет только вклад вот от этих прямоугольников, один из которых мы рассмотрели.
вырезаются те куски, где сечение отлично от нуля. Там, где сечение равно нулю все равно в интеграл вклада никакого не будет (если сечение равно нулю). Будет только вклад вот от этих прямоугольников, один из которых мы рассмотрели.
А теперь давайте на знаменатель (3.40) посмотрим. В знаменателе стоит макроскопическая замедляющая способность. Тут зависимость будет противоположная. Вот если мы, допустим, эту макроскопическую замедляющую способность будем уменьшать, а количество урана оставим без изменения. Т.е. концентрация r8 будет постоянна, а качество замедлителя, допустим, x будем менять. Был легкий замедлитель, у которого x было большое, например, углерод или водород, неважно. А мы заменим его на свинец или уран, к примеру.xсразу стало во много раз меньше. Формально видно, что если знаменатель уменьшается, то показатель степени растет - значит, вероятность поглощения растет, а вероятность избежать рассеяния будет падать. Это чисто формально. А в чем физическая причина? Помните, когда мы рассматривали баланс нейтронов – сколько нейтронов попадает в интервал и сколько выходит из интервала – или если даже взять определение вероятности поглощения – в числителе у нас было количество поглощенных нейтронов - r8×s×DU, а в знаменателе - xSs. Значит, при том же количестве поглощенных нейтронов в резонансе, когда xSsмаленькое и подходит мало нейтронов (плотность замедления мала), вероятность поглощения увеличивается. Если поглощается одно и то же количество нейтронов – ну вот как по трубопроводу у нас расход уменьшается – а дырка, через которую идет утечка, та же самая. Значит, вероятность утечки возрастает. Это отсюда тоже видно. Что у нас здесь как бы не прозрачно? В этот эффективный резонансный интеграл входит и макроскопическое сечение рассеяния (в знаменателе), и микроскопическое сечение поглощения. И это делает несколько неопределенным ответ на вопрос, а что будет, если, допустим, концентрация r8 растет? Потому что когда растет концентрация r8 в экспоненте (19.30), то она и в эффективном резонансном интеграле (в знаменателе) растет. Значит, эффективный резонансный интеграл будет уменьшаться. Т.е. получается что, с одной стороны, один сомножитель при увеличении r8 увеличивается, а второй сомножитель при увеличении r8 будет уменьшаться. Но, поскольку в знаменателе для эффективного резонансного интеграла (19.28) r8 не в чистом виде входит (там единичка есть), то в общем случае зависимость Jэффот r8 будет более слабая, т.е. Jэфф будет медленнее уменьшаться с ростом r8, чем будет увеличиваться знаменатель j от r8. Т.е. если в показателе экспоненты r8 прямо увеличилось в два раза, значит, оно двойку и дает. А когда в Jэффr8 в знаменателе (19.28) увеличивается в двойку, то надо смотреть, насколько это отношение по сравнению с единицей большое. Тенденция есть, но количественно определить трудно.
Дальше нам надо посмотреть, как эффективный резонансный интеграл 238U зависит от этого параметра. Введем новое обозначение 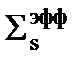 , которое называется эффективным сечением рассеяния, которое равно
, которое называется эффективным сечением рассеяния, которое равно
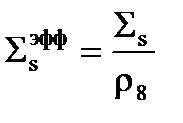 . (3.41)
. (3.41)
Т.е. эффективное сечение рассеяния равно истинному макроскопическому сечению рассеяния, деленному на концентрацию ядер 238U. Дальше, конечно, можно раскрыть выражение (3.41), это будет просто
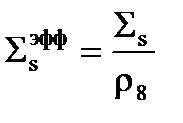 =
= 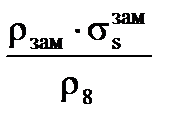 . (3.42)
. (3.42)
Подставим выражение 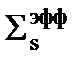 в (19.28), тогда
в (19.28), тогда 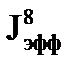 будет равно
будет равно
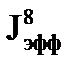 =
= 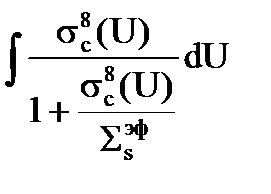 . (3.43)
. (3.43)
Из этого определения видно, что эффективный резонансный интеграл зависит от концентрации ядер 238U, т.е. от концентрации ядер поглотителя или, другими словами, от эффективного макроскопического сечения рассеяния.
Давайте рассмотрим формулу (3.40) дляj и проанализируем два крайних случая - когда концентрация ядер 238U стремится к нулю, т.е. резонансного поглотителя очень мало (среда в основном состоит из замедлителя), а потом наоборот – замедлителя мало, а поглотителя много.
Итак, первый случай, r8® 0. Что будет в этом случае с эффективным резонансным интегралом поглощения? 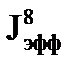 к чему будет стремиться? Мы видим, что r8 стоит в знаменателе (3.38), оно стремится к нулю, значит, дробь можно зачеркнуть, единица так и остается, значит, интеграл
к чему будет стремиться? Мы видим, что r8 стоит в знаменателе (3.38), оно стремится к нулю, значит, дробь можно зачеркнуть, единица так и остается, значит, интеграл 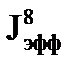 будет стремиться к выражению
будет стремиться к выражению
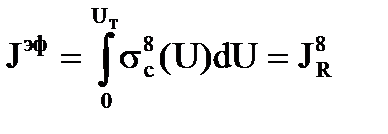 . (3.44)
. (3.44)
Вот эта величина 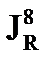 называется истинный резонансный интеграл поглощения (а не эффективный). Это как ядерная константа – истинный резонансный интеграл поглощения нейтронов 238U. Просто
называется истинный резонансный интеграл поглощения (а не эффективный). Это как ядерная константа – истинный резонансный интеграл поглощения нейтронов 238U. Просто 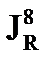 , слова эффективный там нет. Потому что он не зависит от реактора, это ядерная константа, вы видите, туда ничего не входит, кроме сечения. Т.е. это интеграл от сечения захвата по всей области летаргии (или энергии, все равно), вся площадь. Истинные резонансные интегралы поглощения почти для всех ядер или изотопов уже измерены и их можно найти в любых справочниках ядерных констант. Также, как для тепловых нейтронов есть колонка - сечение захвата тепловых нейтронов при энергии 0,025 эВ, так же есть данные по резонансным интегралам.
, слова эффективный там нет. Потому что он не зависит от реактора, это ядерная константа, вы видите, туда ничего не входит, кроме сечения. Т.е. это интеграл от сечения захвата по всей области летаргии (или энергии, все равно), вся площадь. Истинные резонансные интегралы поглощения почти для всех ядер или изотопов уже измерены и их можно найти в любых справочниках ядерных констант. Также, как для тепловых нейтронов есть колонка - сечение захвата тепловых нейтронов при энергии 0,025 эВ, так же есть данные по резонансным интегралам.
Что же получается, когда r8 ® 0? Когда мы стремим r8 к нулю, и Jэфф переходит просто в Jr, то тогда мы можем записать, что
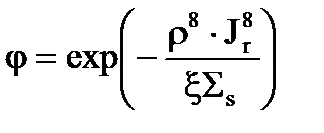 при r8® 0. (3.45)
при r8® 0. (3.45)
Воспользуемся тем, что r8 очень мало. Значит, весь показатель много меньше единицы, и мы воспользуемся разложением экспоненты в ряд. Т.е. если мы имеем функцию вида 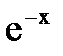 , то при х << 1 (х ® 0), это будет просто 1 – х. Т.е. в данном случае
, то при х << 1 (х ® 0), это будет просто 1 – х. Т.е. в данном случае
х = 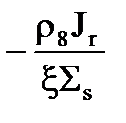 .
.
Раз мы рассматриваем r8® 0, значит, х << 1. Тогда, если воспользоваться этим разложением экспоненты в ряд, мы получим, что
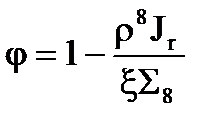 . (3.46)
. (3.46)
Таким образом, для случая, когда r8® 0 дляj получается очень простая формула.
Видно, что вероятность захвата прямо пропорциональна концентрации ядер 238U. Вот для этого мы и сделали здесь это разложение, чтобы убедиться, что когда резонансного поглотителя мало (мала концентрация238U), то вероятность поглощения прямо пропорциональна концентрации ядер 238U.
Теперь давайте рассмотрим другой крайний случай, когда, наоборот, концентрация ядер 238U большая (т.е. r8 будем считать как бы критерием)
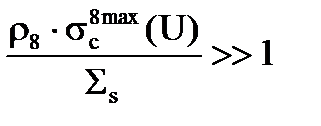 , (3.47)
, (3.47)
здесь 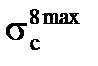 - самое максимальное сечение из всех резонансов. Пусть r8 настолько велико, что все вот это выражение (3.47) много больше единицы Т.е. рассматриваем другой крайний случай – больших концентраций 238U.
- самое максимальное сечение из всех резонансов. Пусть r8 настолько велико, что все вот это выражение (3.47) много больше единицы Т.е. рассматриваем другой крайний случай – больших концентраций 238U.
Во что тогда превратится эффективный резонансный интеграл? Если величина (3.47) много больше единицы, то в знаменателе (3.38) единицей можно пренебречь. В этом случае в (3.38) можно сократить 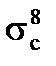 , тогда
, тогда 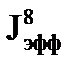 вообще от
вообще от 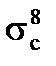 не будет зависеть
не будет зависеть
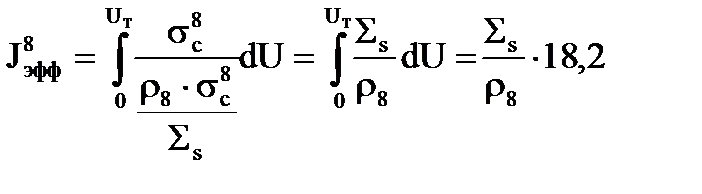 , (3.48)
, (3.48)
т.к. 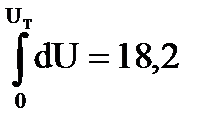 .
.
Важно одно, когда r8 очень большое и оно много больше единицы, эффективный резонансный интеграл 238U просто равен величине 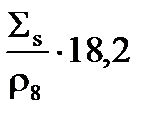 .
.
Если теперь подставить выражение (4.48) в формулу дляj, получится
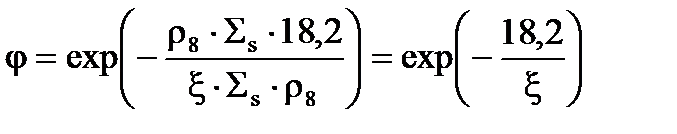 . (3.49)
. (3.49)
Мы знаем, что 18,2/x - это число столкновений, которое необходимо для замедления нейтронов. Помните, когда мы брали полный интеграл летаргии 18,2 и делили на среднюю потерю летаргии при одном столкновении (среднелогарифмическую потерю), мы получали полное число столкновений. Тогда выходит, что в случае, когда замедлителя мало, а 238U много, 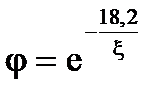 .
.
Итак, пришли к тому, что если концентрация ядер 238U очень маленькая, то тогда вероятность поглощения нейтронов пропорциональна концентрации ядер 238U, а j близко к единице и равно соотношению (3.46), которое много меньше единицы.
Другой крайний случай – когда концентрация ядер 238U большая, тогда вероятность избежать захвата очень маленькая.
Но что здесь интересно? Что j в этом случае не зависит от концентрации ядер 238U, т.е. когда мы начинаем увеличивать концентрацию ядер 238U, у нас вероятность поглощения сначала растет линейно, потом все медленнее и медленнее, потом становится очень большой и перестает вообще зависеть от концентрации ядер 238U. Чисто формально мы это сейчас получили. А теперь надо понять, почему получилась такая математическая ситуация, с какими процессами, происходящими с нейтронами, это связано? Сейчас мы должны подойти к фактору самоэкранирования потока нейтронов.
Чтобы у вас было более полное представление о том, как ведет себя эффективный резонансный интегралпоглощения 238U, нарисуем график зависимость 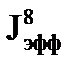 от
от 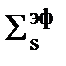 - эффективного сечения рассеяния, которое мы ввели (3.41).
- эффективного сечения рассеяния, которое мы ввели (3.41).
Jэфф(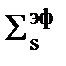 ), барн ), барн
|
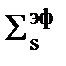 , барн , барн
|
| r8 |
| 0 |
| 50 |
| 200 |
| 9,2 |
| J~240 |
| Рис. 3.9 Резонансный интеграл урана в зависимости от эфф. сечения рассеяния |
На рис. 3.9, если
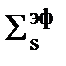 растет вправо, то r8, наоборот, растет влево. Потому что большое
растет вправо, то r8, наоборот, растет влево. Потому что большое 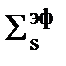 соответствует очень маленькой концентрации ядер 238U. Мы на этом графике можем рассмотреть крайний случай, когда замедлителя вообще нет, есть чистый металлический 238U, но у него есть свое сечение рассеяния ~ 8 барн (оно играет роль), и тоже есть макроскопическое сечение рассеяния. Вот в этом случае, если нет замедлителя, эффективный резонансный интеграл поглощения имеет минимальное значение, равное 9,2 барн.
соответствует очень маленькой концентрации ядер 238U. Мы на этом графике можем рассмотреть крайний случай, когда замедлителя вообще нет, есть чистый металлический 238U, но у него есть свое сечение рассеяния ~ 8 барн (оно играет роль), и тоже есть макроскопическое сечение рассеяния. Вот в этом случае, если нет замедлителя, эффективный резонансный интеграл поглощения имеет минимальное значение, равное 9,2 барн.
Так вот, если теперь разбавлять 238U замедлителем и рассмотреть другой крайний случай, когда эффективный резонансный интеграл переходит в истинный, или, как его еще называют «при бесконечном разбавлении» урана замедлителем (концентрация 238U мала, в основном среда состоит из замедлителя), то тогда можно видеть, что 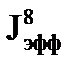 достигает своего максимального значения
достигает своего максимального значения 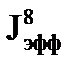 = 240барн. Т.е. если взять сечение захвата, которое вы видели на графике и проинтегрировать, то получится 240 барн. Вот это диапазон изменения эффективного резонансного интеграла - от минимального значения, когда нет замедлителя, есть только собственное упругое рассеяние на 238U, до максимального значения, когда смесь очень разбавлена - замедлителя много, а урана мало.
= 240барн. Т.е. если взять сечение захвата, которое вы видели на графике и проинтегрировать, то получится 240 барн. Вот это диапазон изменения эффективного резонансного интеграла - от минимального значения, когда нет замедлителя, есть только собственное упругое рассеяние на 238U, до максимального значения, когда смесь очень разбавлена - замедлителя много, а урана мало.
Все гомогенное, то, что мы рассматриваем – все гомогенное.
И теперь нам надо уже рассмотреть по существу - почему наблюдается такое явление - с увеличением концентрации ядер 238U вероятность поглощения сначала растет линейно, потом все медленнее и медленнее, а потом вообще перестает зависеть от концентрации ядер 238U. Для этого надо ввести в рассмотрение еще одно понятие – плотность столкновений. Вот мы рассматривали плотность замедления нейтронов, а сейчас надо ввести в рассмотрение плотность столкновений. Если сказать словами, что такое плотность столкновений, так это количество нейтронов, сталкивающихся в 1 с в 1 см3с ядрами любым способом – с захватом, с делением, с рассеянием – неважно, что – т.е. это полное число столкновений (обозначается буквой Y(U)). И поэтому Y(U) будет равняться потоку нейтронов, умноженному на полное сечение, помните, мы вводили St - полное макроскопическое сечение, куда входят любые процессы – рассеяние, поглощение, деление
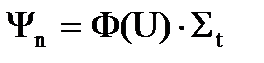 . (3.50)
. (3.50)
Плотность столкновений – это количество нейтронов, сталкивающихся в 1 с в 1 см3 любым способом со всеми ядрами, которые находятся в этом кубическом сантиметре. И неважно, что произойдет после столкновения – рассеяние, захват, деление. Поэтому в количество столкновений входит полное сечение взаимодействий St макроскопическое, которое определяется как сумма всех частных сечений – деление, захват, рассеяние – неважно. В нашем случае это только два типа процессов – упругое рассеяние на замедлителе и поглощение, скажем, на 238U. Т.е. мы можем записать, более подробно, что Y(U) равно потоку нейтронов, умноженному на Ss + Sс(U)
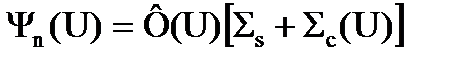 , (3.51)
, (3.51)
Sс(U) – зависит от U, а Ss от U не зависит. Мы приняли с вами, что сечение рассеяния от энергии практически не зависит.
Так вот, оказывается, что эта величина, плотность столкновений нейтронов Y(U), очень слабо зависит от летаргии. Вот сечение захвата Sс(U), так же, как полное сечение, может очень сильно меняться от U, а плотность столкновений очень слабо зависит от летаргии. Если это принять, то тогда можно записать, что поток нейтронов от летаргии пропорционален обратной величине сечений Ss + Sс(U)
| Ф(U) |
| Sс<<Ss |
| Sс=Ss |
| Sс>>Ss |
| U1 |
| U |
| Рис. 3.10 |
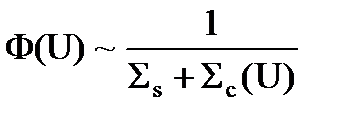 . (3.52)
. (3.52)
Нарисуем график и посмотрим, как будет вести себя поток нейтронов Ф(U) от летаргии U при прохождении резонанса (рис. 3.10). Допустим, U1 - это резонанс. Поток нейтронов в областях, где нет резонанса, где sс = 0, (вдали от резонанса) – это постоянная величина. Когда мы подходим к резонансу, то в резонансе поток нейтронов имеет провал и дальше (после провала) поднимается. Но если на резонансе был захват, то поток нейтронов после резонанса будет чуть-чуть меньше.
| U1 |
| U |
| Рис. 3.11 |
| St |
Теперь рассмотрим, как это зависит от концентрации ядер 238U. Для этого нам нужно нарисовать график зависимости полного макроскопического сечения от летаргии для различных случаев. Допустим, St(U) в этой области постоянно, потом идет резонанс U1. Дальше полное сечение идет постоянно. Потому что оно определяется полностью сечением рассеяния (там, где нет поглощения), а сечение рассеяния постоянно. Дальше мы будем наблюдать пик, потом снижение и сечение вот так идет. Величина этого пика будет зависеть от того, много или мало ядер 238U. Т.е. может быть случай, когда это увеличится вот так, а может быть случай и вот так. Значит, вот это будет случай 1, когда r8 мало, когда r8 мало, то эта добавка маленькая и полное сечение почти равно сечению рассеяния. Скажем, если в два раза выросла, то это случай, когда
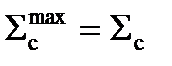 . Т.е. вот эта величина у нас фактически удвоилась – это есть
. Т.е. вот эта величина у нас фактически удвоилась – это есть 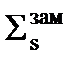 . Потому что это полное сечение, но оно здесь равно
. Потому что это полное сечение, но оно здесь равно 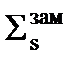 . Когда мы подходим к резонансу и r8 мало, очень мало добавляется и st чуть-чуть увеличивается. Вот если оно увеличилось в 2 раза, то в 2 раза – это как раз вот эта добавка, она обязана Sс. Потому что если Sс макроскопическое максимальное какраз равно Ss, то тогда полное сечение становится в 2 раза больше. Было Ss, а еще стало Sс, которое как раз равно Ss. Поэтому в 2 раза больше.
. Когда мы подходим к резонансу и r8 мало, очень мало добавляется и st чуть-чуть увеличивается. Вот если оно увеличилось в 2 раза, то в 2 раза – это как раз вот эта добавка, она обязана Sс. Потому что если Sс макроскопическое максимальное какраз равно Ss, то тогда полное сечение становится в 2 раза больше. Было Ss, а еще стало Sс, которое как раз равно Ss. Поэтому в 2 раза больше.
Ну а если и больше, то тем более будет больше. А как на это будет реагировать поток нейтронов? Если мы смотрим на эту формулу, то видим, что поток нейтронов обратно пропорционален полному сечению. Мы можем нарисовать график – вот здесь если поток нейтронов чуть-чуть уменьшается, то вот этот случай соответствует малому поглощению, т.е. это случай, когда Sс<<Ss. Вот этот случай, если я в половину уменьшу, будет соответствовать случаю, когда 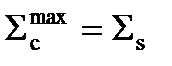 . А вот когда провал почти до нуля идет, то это случай будет наоборот, когда
. А вот когда провал почти до нуля идет, то это случай будет наоборот, когда 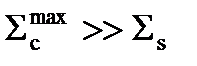 .
.
Содержание ГЛ 3
3 Замедление нейтронов. 1
3.1 Общие закономерности. 1
3.2 Закон рассеяния. 5
3.3 Замедление нейтронов в средах. 8
3.4 Модель непрерывного замедления. Возраст нейтронов. 10
3.5 Диффузионно-возрастное приближение. 13
3.5 Условия критичности реактора в диффузионно-возрастном приближении. 15
3.6 Сравнение свойств различных замедлителей. 16
3.7 Вероятность избежать резонансного захвата при замедлении. 17
3.8 Приближение узкого резонанса. 20
Date: 2015-07-01; view: 1018; Нарушение авторских прав