
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вероятность избежать резонансного захвата при замедлении
|
|
Одной из важнейших задач в промежуточной области замедления является оценка Вероятности избежать резонансного захвата при замедленииj,.
| Uгр |
| 18,2 |
| U |
| Ф(U) |
| Рис.3.7 Спектр нейтронов от летаргии |
Для оценки j- вероятности избежать резонансного захвата важно распределение нейтронов, ведь замедление нейтронов происходит в очень большом широком энергетическом интервале - от МэВ до эВ. Поэтому ввели понятие логарифмической энергии или летаргии нейтронов, чтобы вместо энергии, которая меняется на восемь порядков (от МэВ до сотых эВ), ввести слабоменяющуюся величину летаргии, которая меняется от 0 до 18. Т.е. весь диапазон энергии перекрывается летаргией, изменяющейся всего от 0 до 18.
Если нарисовать поток нейтронов (спектр замедляющихся нейтронов) в зависимости от летаргии (рис. 3.7), то можно видеть следующее: в какой то точке, допустим, при этой энергии, быстрые нейтроны родились, потом идет какой-то поток нейтронов, а дальше начинается область тепловых энергий, здесь спектр отрезается на Uгр, это Uгр соответствует Егр, которое мы ввели ранее.Uгр в единицах летаргии будет равно: Uгр= 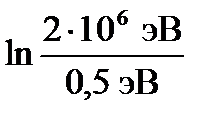 .
.
Для простоты приведём простейшие соображения, позволяющие оценить вероятность избежать резонансного захвата при замедлении. Более строгие и корректные соображения буту приведены в следующем разделе 3.8 «приближение узкого резонанса».
Выделим и рассмотрим сначала один резонанс (мы знаем по графикам, что там резонансов этих сотни, и на каждом из этих резонансов по чуть-чуть идет поглощение). На рис. 3.8а изображен один резонанс но не в масштабе энергии, а в летаргии U, т.е. сечение захвата s 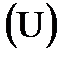 , допустим, на каком-то нулевом резонансе
, допустим, на каком-то нулевом резонансе 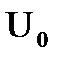 (конечно, на резонансе сечения захвата 238U
(конечно, на резонансе сечения захвата 238U 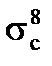 ).
).
В начале координат ноль, значит, замедление идет в сторону возрастания летаргии.
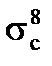
|
| smax |
| 0 |
| U0 |
| U |
| Рис.3.8а Сечение резонанса U-238 в шкале летаргии |
| Замедление |
Как мы определим вероятность поглощения?
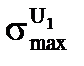
|
| sс |
| DU0 |
| U |
| U0 |
| Рис..3.8 в Модель резонанса «столбик» |
Упростим наши оценки– вместо вот такой действительной кривой 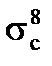 (рис. 3.8а) возьмем модель
(рис. 3.8а) возьмем модель 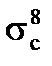 в виде столбика (рис. 3.8.в), но так, чтобы площади под кривыми были равны, в среднем это будет то же самое U0,. Т.е. мы аппроксимируем это сечение
в виде столбика (рис. 3.8.в), но так, чтобы площади под кривыми были равны, в среднем это будет то же самое U0,. Т.е. мы аппроксимируем это сечение 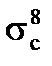 , и будем считать, что вне этого интервала сечения равны нулю, а внутри интервала равны как раз максимуму
, и будем считать, что вне этого интервала сечения равны нулю, а внутри интервала равны как раз максимуму 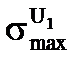 . А ширину столбика назовем шириной резонанса DU0., в ядерной физике оно обозначается как Г0с8.
. А ширину столбика назовем шириной резонанса DU0., в ядерной физике оно обозначается как Г0с8.
Применим нестрогую, но полезную модель «кусков жвачки». Пусть замедление нейтронов моделируется прыжками шариков для пинг-понга по полу коридора. Когда коридор чист 100% шариков от источника допрыгают до конца коридора. При этом «шаг» каждого прыжка мы оценим как x, вероятность рассеяния σs, таким образом нейтроны будут равномерно падать во все интервалы летаргииdu от 0 до тепловых(18), в том числе и в Г. Представим, что резонанс это «жвачка» на полу шириной Г. Вероятность прилипнуть к единственному куску жвачки будет (Г0с8/xσs), а вероятность избежать прилипания равна φ0 =1 -(Г0с8/ xσs). Таково соотношение если в среде находится одно ядро урана-238 и одно ядро замедлителя.
Без доказательства будем считать, что если в среде произвольное число ядер NU и Nзам, то φ0 =1 -(NU Г0с8/ Nзамxσs)
Вспомним, что функция (1-Х) является простейшим приближением exp(-x) при разложении в ряд Тейлора, представим ее
φ0 =ЕХР(-NU Г0с8/ Nзамxσs) (3.22а)
Вспомнив, что резонансов на пути много и вероятность избежать захвата по всей совокупности есть произведение вероятностей:
φ = ∏i{ ЕХР(-NU Гiс8/ Nзамxσs)} (3.22в)
Но произведение экспонент есть сумма их числителей, значит:
φ = ЕХР(-{ Σi[PiNU Гiс8]}/ Nзамxσs) (3.22с)
где Pi – некоторая весовая функция.
Приняв, что весовая функция есть спектр замедления Ферми 1/Е, превратим сумму в интеграл и назовем его «резонансный интеграл при бесконечном разбавлении» (ядер урана ядрами замедлителя:
IU8а,¥ =  òsaU(E)*dE/E (3.22d)
òsaU(E)*dE/E (3.22d)
Равен 240-270 бн.
И окончательно:
φ = ЕХР(-{NUIU8а,¥}/ xΣs) (3.22e)
Ss
Date: 2015-07-01; view: 857; Нарушение авторских прав