
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Градиентные методы
|
|
Градиентные методы относятся к методам первого порядка. Предположим, что минимизируемая функция  определена и непрерывно дифференцируема на пространстве
определена и непрерывно дифференцируема на пространстве 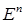 . В градиентных методах для построения последовательности приближений в качестве направлений итерационного перехода выбираются антиградиенты функции
. В градиентных методах для построения последовательности приближений в качестве направлений итерационного перехода выбираются антиградиенты функции  , вычисленные в точках
, вычисленные в точках 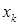 , то есть
, то есть 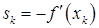 .
.
Таким образом,
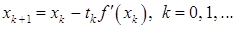 (1)
(1)
Здесь и далее в этом параграфе считаем, что 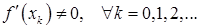 , то есть ни одна точка последовательности
, то есть ни одна точка последовательности 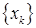 не является стационарной точкой функции
не является стационарной точкой функции  . Легко убедиться, что если точка
. Легко убедиться, что если точка  – не стационарная, то
– не стационарная, то 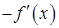 является релаксационным направлением для функции
является релаксационным направлением для функции  в точке
в точке  . Более того, ненулевой антиградиент – это в некотором смысле даже направление наискорейшего убывания. Пояснить такой термин можно следующим образом. Решением задачи миними-зации производной функции
. Более того, ненулевой антиградиент – это в некотором смысле даже направление наискорейшего убывания. Пояснить такой термин можно следующим образом. Решением задачи миними-зации производной функции  дифференцируемой в точке
дифференцируемой в точке  по направлениям на единичном шаре, то есть задачи минимизации линейной функции
по направлениям на единичном шаре, то есть задачи минимизации линейной функции 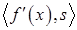 на множестве
на множестве 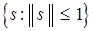 , является вектор
, является вектор 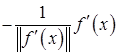 . Поэтому
. Поэтому 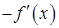 и задает направление наискорейшего убывания функции в точке
и задает направление наискорейшего убывания функции в точке  . Приведенные доводы оправдывают выбор антиградиента как направления итерационного перехода в методах безусловной минимизации. Часто полношаговый градиентный метод называют методом наискорейшего спуска.
. Приведенные доводы оправдывают выбор антиградиента как направления итерационного перехода в методах безусловной минимизации. Часто полношаговый градиентный метод называют методом наискорейшего спуска.
Итак, общее правило генерации последовательности приближений 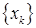 в градиентных методах задается формулой (1). Разновидности градиентных методов отличаются между собой лишь способом выбора шагового множителя
в градиентных методах задается формулой (1). Разновидности градиентных методов отличаются между собой лишь способом выбора шагового множителя 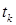 .
.
Наиболее простым из них является метод с постоянным шагом. Пусть задана некоторая константа 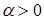 . Положим
. Положим 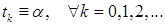 Тогда
Тогда
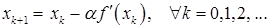
Конечно, при произвольно выбранном значении 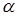 последовательность приближений может оказаться нерелаксационной и даже неминимизирующей. Известны теоремы, в которых сформулированы требования к функции
последовательность приближений может оказаться нерелаксационной и даже неминимизирующей. Известны теоремы, в которых сформулированы требования к функции  , гарантирующие сходимость последовательности приближений при выборе
, гарантирующие сходимость последовательности приближений при выборе 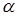 из некоторого промежутка
из некоторого промежутка 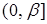 , где
, где 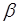 – положительная константа. Однако на практике, как правило, не удается вычислить значение
– положительная константа. Однако на практике, как правило, не удается вычислить значение 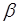 до решения задачи.
до решения задачи.
Тем не менее, этот вариант градиентного метода все же можно использовать на практике, подбирая значение 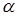 в процессе минимизации. Начальное значение
в процессе минимизации. Начальное значение 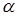 выбирается произвольно. На каждой итерации метода проверяется неравенство
выбирается произвольно. На каждой итерации метода проверяется неравенство 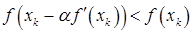 . Если оно выполняется, полагаем
. Если оно выполняется, полагаем 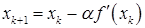 , и значение
, и значение 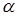 остается неизменным. Если же на какой-то итерации
остается неизменным. Если же на какой-то итерации 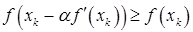 (то есть значение шагового множителя было выбрано слишком большим), заменим его, например, на
(то есть значение шагового множителя было выбрано слишком большим), заменим его, например, на 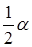 . Очевидно, что количество дроблений величины
. Очевидно, что количество дроблений величины 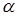 конечно – дробления
конечно – дробления 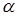 прекратятся, как только при некотором значении
прекратятся, как только при некотором значении 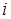 выполнится неравенство
выполнится неравенство 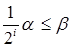 . С этого момента метод становится методом с постоянным шагом.
. С этого момента метод становится методом с постоянным шагом.
Главное преимущество этого варианта мето-да – простота нахождения шагового множителя. Недостатком же его является то, что для получения заданной точности зачастую требуется очень большое число итераций. Поэтому градиентный метод с постоянным шагом обычно используют для решения сравнительно простых задач, где число переменных невелико, время, отпущенное на решение задачи, не лимитировано, и не требуется высокой точности вычисления решения. В противном случае используют более совершенные методы, позволяющие достичь той же точности за меньшее число итераций. Примером такого метода является полношаговый градиентный ме-тод.
Как видно из названия, в этой разновидности метода шаговый множитель определяется как полный, то есть
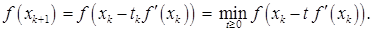
Заметим, что одномерная минимизация осуществляется здесь не по всей числовой оси, а только на неотрицательной полуоси, так как направление итерационного перехода является релаксационным. Очевидно, что последовательность, генерируемая этим вариантом градиентного метода, является релаксационной.
Остановимся на изучении полношагового градиентного метода несколько подробнее.
Определение 1. Пусть функция  определена и дифференцируема на
определена и дифференцируема на 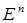 . Говорят, что ее градиент
. Говорят, что ее градиент 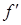 удовлетворяет на
удовлетворяет на 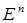 условию Липшица, если существует константа
условию Липшица, если существует константа 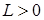 (константа Липшица) такая, что
(константа Липшица) такая, что
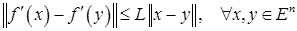 .
.
Приведем следующую лемму.
Лемма 1. Пусть функция  определена и дифференцируема на
определена и дифференцируема на 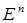 , ее градиент
, ее градиент 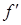 удовлетворяет на
удовлетворяет на 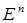 условию Липшица. Тогда для любых
условию Липшица. Тогда для любых 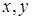 выполняется неравенство
выполняется неравенство
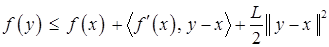 . (1)
. (1)
На основе этой леммы получим оценку приращения функции на луче 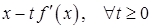 .
.
Для этого в (1) положим 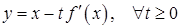 . Получим
. Получим
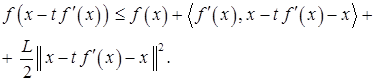
После преобразований для всех 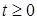 имеем
имеем
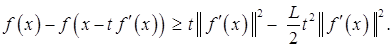
Откуда
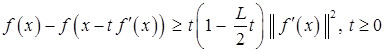 . (2)
. (2)
Теорема 1. (Общая теорема сходимости полношагового градиентного метода)
Пусть функция  определена, дифференцируема и ограничена снизу на
определена, дифференцируема и ограничена снизу на 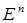 , ее градиент
, ее градиент 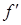 удовлетворяет на
удовлетворяет на 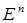 условию Липшица, последовательность
условию Липшица, последовательность  , построена по правилам полношагового градиентного метода, где
, построена по правилам полношагового градиентного метода, где 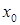 – произвольный вектор из
– произвольный вектор из 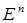 . Тогда
. Тогда 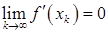 .
.
Доказательство. В неравенстве (2) положим
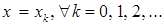 Получим для всех
Получим для всех 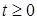
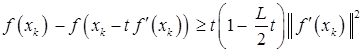 . Отсюда в силу выбора шагового множителя
. Отсюда в силу выбора шагового множителя 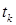 имеем
имеем
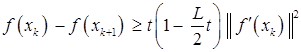 ,
, 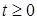 . В этом неравенстве положим
. В этом неравенстве положим 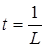 . Получим
. Получим
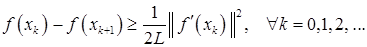 (3)
(3)
Так как последовательность  , является релаксационной, и функция
, является релаксационной, и функция  ограничена снизу на
ограничена снизу на 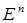 , то последовательность
, то последовательность 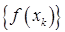 сходится. Следовательно,
сходится. Следовательно, 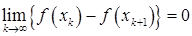 . Отсюда и из (3)
. Отсюда и из (3) 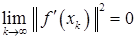 . Откуда и следует утверждение теоремы.
. Откуда и следует утверждение теоремы.
Теорема 2. Пусть выполняются все условия теоремы 1 и последовательность 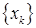 ,
, 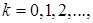 имеет предельную точку
имеет предельную точку 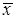 . Тогда
. Тогда 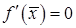 .
.
Доказательство. Так как 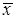 – предельная точка последовательности
– предельная точка последовательности  , то существует подпоследовательность
, то существует подпоследовательность 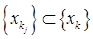 такая, что
такая, что 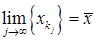 . В силу теоремы 1 и непрерывности
. В силу теоремы 1 и непрерывности 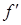 имеем
имеем
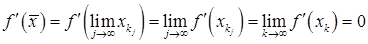 .
.
Что и требовалось.
Таким образом, в условиях теоремы 2 любая предельная точка последовательности приближений является стационарной точкой функции  .
.
Теорема 3. (Теорема сходимости полно-шагового градиентного метода для выпуклых функций)
Пусть выполняются все условия теоремы 1. Если, кроме того, функция  выпукла и множество
выпукла и множество 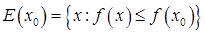 ограничено, то безусловный минимум функции
ограничено, то безусловный минимум функции  достигается, последовательность
достигается, последовательность  , имеет предельные точки, любая ее предельная точка является точкой минимума функции
, имеет предельные точки, любая ее предельная точка является точкой минимума функции  , и последова-тельность
, и последова-тельность 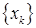 является минимизирующей.
является минимизирующей.
Доказательство. Множество 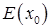 замкнуто в силу непрерывности функции
замкнуто в силу непрерывности функции  и ограничено, поэтому безусловный минимум функции
и ограничено, поэтому безусловный минимум функции  до-стигается.
до-стигается.
В силу релаксационности последовательности 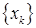 выполняется включение
выполняется включение 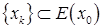 . Тогда, в силу замкнутости и ограниченности множества
. Тогда, в силу замкнутости и ограниченности множества 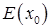 , последовательность
, последовательность 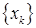 имеет предельные точки.
имеет предельные точки.
Пусть 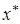 – одна из этих предельных точек. Из теоремы 2 следует, что
– одна из этих предельных точек. Из теоремы 2 следует, что 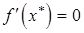 . Это –достаточное условие безусловного минимума вы-
. Это –достаточное условие безусловного минимума вы-
пуклой функции  . Таким образом,
. Таким образом, 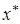 – точка безусловного минимума функции
– точка безусловного минимума функции  .
.
Убедимся, наконец, что 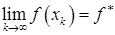 . Пусть подпоследовательность
. Пусть подпоследовательность 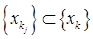 такова, что
такова, что 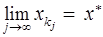 . Тогда в силу непрерывности функции
. Тогда в силу непрерывности функции  и сходимости последовательности
и сходимости последовательности 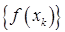 ,
,
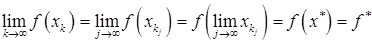 .
.
Что и требовалось.
Теорема 4. Пусть выполняются все условия
теоремы 3, и функция  имеет единственную точку безусловного минимума
имеет единственную точку безусловного минимума 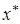 . Тогда
. Тогда 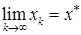 .
.
Доказательство. Пусть это не так. Тогда последовательность 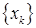 имеет еще одну предельную точку
имеет еще одну предельную точку 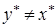 . Но, как следует из теоремы 3,
. Но, как следует из теоремы 3, 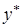 – также точка безусловного минимума функции
– также точка безусловного минимума функции  , что противоречит условию теоремы. Полученное противоречие и доказывает теорему.
, что противоречит условию теоремы. Полученное противоречие и доказывает теорему.
Заметим, что условие этой теоремы может выполняться, например, в случае строгой выпук- лости функции  .
.
Кроме изученных здесь вариантов градиентного метода известно большое количество и других модификаций этого метода, многие из которых часто используются на практике. Остановимся вкратце на некоторых из них.
Во-первых, вариант метода, в котором шаговый множитель 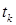 находится из условий
находится из условий 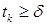 и
и
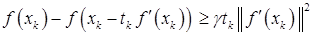 (4)
(4)
при некотором достаточно малом 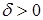 и любом
и любом 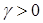 . Для отыскания значения
. Для отыскания значения 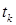 , удовлетворяющего неравенству (4), используют следующий прием. Выберем произвольное значение
, удовлетворяющего неравенству (4), используют следующий прием. Выберем произвольное значение 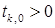 . Если для него неравенство (4) не выполняется (значение
. Если для него неравенство (4) не выполняется (значение 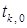 слишком велико), то положим
слишком велико), то положим 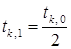 и
и
проверим, удовлетворяет ли 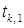 неравенству (4). Если нет, то процесс дробления продолжим. Можно показать, что в условиях теоремы 1 количество таких дроблений конечно. Пусть i – наименьшее целое число, для которого величина
неравенству (4). Если нет, то процесс дробления продолжим. Можно показать, что в условиях теоремы 1 количество таких дроблений конечно. Пусть i – наименьшее целое число, для которого величина 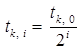 удовлетворяет неравенству (4), тогда положим
удовлетворяет неравенству (4), тогда положим 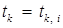 . Если же начальное значение
. Если же начальное значение 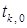 удовлетворяет неравенству (4), то желательно попытаться увеличить его значение, полагая
удовлетворяет неравенству (4), то желательно попытаться увеличить его значение, полагая 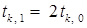 . Количество умножений также конечно. Пусть
. Количество умножений также конечно. Пусть 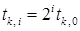 удовлетворяет неравенству (4), а
удовлетворяет неравенству (4), а 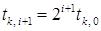 не удовлетворяет. Тогда положим
не удовлетворяет. Тогда положим
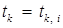 . Для уменьшения количества дроблений либо умножений полезно выбирать
. Для уменьшения количества дроблений либо умножений полезно выбирать 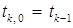 , а значение
, а значение 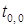 выбирается произвольно.
выбирается произвольно.
Во-вторых, вариант метода, в котором шаговый множитель 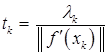 ,
, 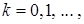 где
где 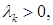
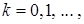
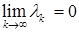 ,
, 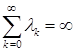 . Заметим, что в этом случае градиентный метод генерирует нерелаксационную, вообще говоря, последовательность приближений.
. Заметим, что в этом случае градиентный метод генерирует нерелаксационную, вообще говоря, последовательность приближений.
Наконец, приведем еще один вариант метода, который используется в случае, когда известно минимальное значение функции 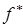 . В этом случае шаговый множитель вычисляется по формуле
. В этом случае шаговый множитель вычисляется по формуле 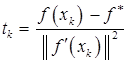 ,
, 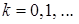 В этой точке касательная к графику функции
В этой точке касательная к графику функции 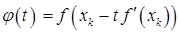 , построенная в точке
, построенная в точке 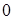 , принимает значение
, принимает значение  .
.
В заключение параграфа коротко опишем метод сопряженных градиентов (метод Флетчера-Ривса). Его можно отнести к группе методов первого порядка и, в то же время, к методу сопряженных направлений. Пусть матрица 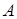 является симметричной и положительно определенной, функция
является симметричной и положительно определенной, функция 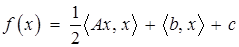 . В
. В
этом методе направление итерационного перехода 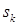 вычисляется по формулам
вычисляется по формулам
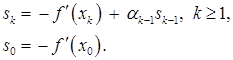 (5)
(5)
Таким образом, 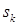 – это линейная комбинация градиента функции
– это линейная комбинация градиента функции  в точке
в точке 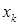 и предыдущего направления
и предыдущего направления  . Множитель
. Множитель 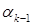 находится из требования сопряженности векторов
находится из требования сопряженности векторов 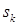 и
и  относительно матрицы
относительно матрицы 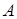
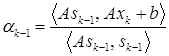 .
.
Тогда 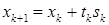 , где шаг находится как полный, то есть
, где шаг находится как полный, то есть
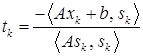 .
.
Векторы 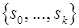 , полученные по формулам (5), попарно сопряжены относительно матрицы
, полученные по формулам (5), попарно сопряжены относительно матрицы 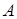 . Поэтому данный метод позволяет за конечное число итераций отыскать безусловный минимум функции
. Поэтому данный метод позволяет за конечное число итераций отыскать безусловный минимум функции  .
.
Этот метод применяется также и для минимизации неквадратичных функций. Для этих целей формулам для нахождения коэффициента 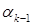 придают следующий вид:
придают следующий вид:
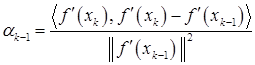 ,
,
или
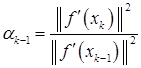 .
.
Несмотря на то, что для неквадратичных функций метод сопряженных градиентов уже не является конечным, он – один из наиболее используемых методов безусловной минимизации.
| <== предыдущая | | | следующая ==> |
| Методы сопряженных направлений | | | Метод Ньютона |
Date: 2015-06-12; view: 1188; Нарушение авторских прав