Метод Ньютона

В этом параграфе мы познакомимся с методом Ньютона, который был разработан одним из первых в группе методов второго порядка. Пусть функция 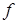определена и дважды дифференцируема на 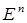. Пусть найдены векторы 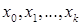. Опишем правила вычисления следующего элемента последовательности приближений. Так как функция 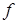дважды дифференцируема, то квадратичная часть ее приращения 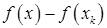в окрестности точки 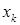имеет вид

.

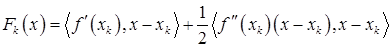Здесь 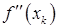– матрица вторых частных производ-ных функции 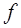в точке .

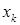Пусть функция 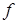такова, что квадратичная функция 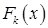имеет единственную точку безусловного минимума. Положим

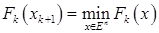. (1)

Равенство (1) и определяет правило построения последовательности приближений методом Ньютона.

Прежде чем обсуждать возможности численной реализации этого метода проведем некоторые построения. Градиент функции 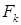имеет вид

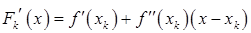. Так как вектор 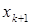является безусловным минимумом функции 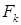, то 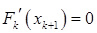, то есть

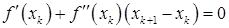. (2)

Таким образом, вектор 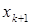является решением системы линейных алгебраических уравнений

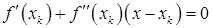. (3)

Из единственности решения задачи (1) следует невырожденность матрицы 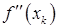. Поэтому существует обратная ей матрица 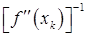. Тогда из равенства (2) получим

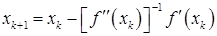. (4)

Итак, мы получили три соотношения (1), (2) и (4), определяющие вектор 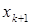. На этих равенствах основаны три группы численно реализуемых алгоритмов метода Ньютона.

Первая задается формулой (1). В зависимости от выбора того или иного метода безусловной минимизации функции 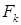получаются различные алгоритмы этой группы. Для этих целей можно применять, например, методы прямого поиска либо методы первого порядка, изученные в предыдущих параграфах.

Вторая группа алгоритмов основана на решении системы уравнений (3). Существует боль-шое количество методов решения таких систем. В каждом конкретном случае имеется возможность подобрать подходящий метод. В результате будут получены различные численно реализуемые алгоритмы. Такой подход к отысканию приближения 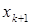– один из самых используемых на практике.

Наконец, формула (4) также может быть положена в основу алгоритмов нахождения 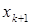. Для этого необходимо использовать те или иные методы обращения матрицы 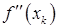. Однако, главная ценность формулы (4) в удобстве ее использования при анализе последовательности приближений, вырабатываемой методом Ньютона, а также для разработки различных модификаций этого метода. В частности, легко увидеть, что метод Ньютона укладывается в общую схему итерационных методов 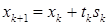, где , .

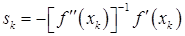Метод Ньютона имеет ряд положительных особенностей. При помощи этого метода зачастую удается за небольшое количество итераций получать решение задачи на безусловной минимум с высокой точностью. Однако как теоретическое обоснование этого метода, так и опыт его практического применения показывают на ряд больших сложностей в реализации метода. Показано, что метод применим лишь при некоторых дополнительных требованиях к целевой функции и начальному приближению 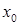.Вспомогательная задача, решаемая на каждой итерации, требует значительных вычислительных затрат независимо от варианта используемого алгоритма. Подробное обсуждение всех перечисленных проблем не входит в рамки первого знакомства с этим методом в нашем пособии. Следует иметь в виду, что эти проблемы труднопреодолимы, а их игнорирование может сделать применение метода бесполезным.

Большое количество работ посвящено развитию метода Ньютона. Известны различные модификации этого метода, поэтому первоначальный вариант метода, изложенный выше, часто называют классическим методом Ньютона.

Модификации можно разделить на две группы. Во-первых, это методы, которые ценой еще большего усложнения позволяют устранить некоторые отрицательные особенности классического метода Ньютона. Примером такого метода является так называемый модифицированный метод Ньютона. Как отмечалось выше, в классическом варианте метода шаговый множитель равен единице. В модифицированном методе Ньютона формула, задающая правило построения последовательности приближений, приобретает вид

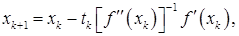
где шаговый множитель 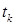определяется как пол-ный, то есть путем одномерной минимизации

.

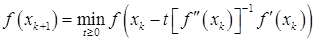Конечно, такая модификация заметно увеличивает объем вычислений на каждой итерации метода, поскольку теперь кроме решения подзадачи отыскания направления итерационного перехода на каждой итерации решается еще одна вспомогательная задача отыскания шагового множителя. Однако у модифицированного метода имеются значительные преимущества. Главное – это то, что начальное приближение 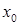может быть произвольным, а также существенно ослабляются требования к свойствам функции f. Таким образом, диапазон применимости метода становится значительно шире. Заметим, что в модифицированном методе 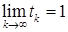, то есть «модифицированный метод в пределе превращается в классический». Поэтому можно на некоторой итерации переключить построение последовательности приближений с модифицированного метода на классический, что позволит уменьшить затраты на осуществление итерации без потери «качества приближений».

Другое направление модификаций основано на замене обратной матрицы 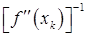некоторой ее аппроксимацией 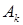, что заметно упрощает выполнение каждой итерации и расширяет область применения таких методов. Тогда прави-

ло построения последовательности приближений принимает вид

,

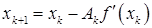где 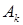– симметричная квадратная матрица. Суще-ствует большое количество различных процедур вычисления этих матриц. Методы этой группы называются квазиньютоновскими. Они заметно проще в реализации по сравнению с классическим методом Ньютона, но мало чем уступают ему по эффективности. Поэтому среди современных методов безусловной минимизации квазиньютоновские методы – одни из наиболее используемых.

Date: 2015-06-12; view: 490; Нарушение авторских прав