Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Методы сопряженных направлений
|
|
В этом параграфе будем считать, что дана симметричная положительно определенная матрица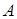 
размерности 
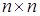. Введем следующие понятия.
Определение 1. Ненулевые векторы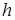 
и 
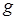называются сопряженными относительно матрицы 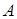( 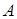- сопряженными), если выполняется
равенство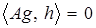 
.
Например, ортогональные векторы сопряжены относительно единичной матрицы.
Определение 2. Систему векторов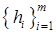 
называют сопряженной относительно матрицы 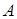, если любые два различных вектора в ней являются 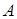- сопряженными.
Теорема 1. Любая система векторов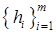
сопряженная относительно матрицы 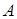является линейно независимой.
Доказательство. Пусть числа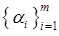 
таковы что
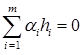. (1)
Выберем произвольный номер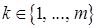 
и умножим равенство (1) на вектор 
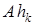. Получим 
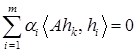. Отсюда в силу попарной сопряженности векторов системы 
имеем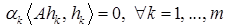 
. Следовательно, в силу положительной определенности матрицы 
, 
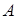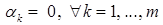. Откуда и следует линейная независимость системы векторов .
Заметим, что из теоремы 1 следует, что система содержит не более 
векторов. Поэтому если 
, то система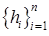 
является базисом пространства 
.
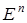Пусть дана задача безусловной минимизации квадратичной функции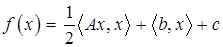 
, пусть 
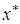– минимум функции 
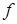. В силу положительной определенности матрицы 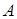функция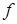
строго выпукла, а значит, минимум единственен. Согласно необходимым и достаточным условиям минимума выпуклой функции 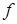имеем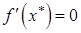 
, то есть
. (2)
Пусть система векторов 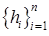сопряжена относительно матрицы 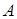. Тогда согласно теореме 1 она образует базис в 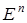. Значит, для любой фиксированной точки 
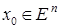существуют числа 
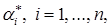такие что
. (3)
Отсюда и из (2)
. (4).
Выберем произвольный номер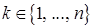 
, умно-жим (4) на вектор 
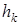и с учетом попарной сопряженности векторов системы 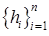получим
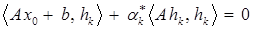, откуда
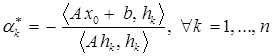. (5)
Таким образом, с помощью базиса 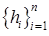, состоящего из векторов, сопряженных относи-
тельно матрицы 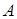, вектор 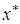может быть найден по явным формулам (5).
Найдем формулу для вычисления полного шага для функции 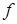из точки 
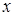по направлению 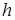. Для этого потребуем, чтобы производная в точке 
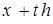по направлению 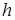равнялась нулю: 
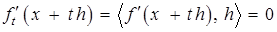. Тогда имеем 
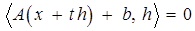. Решая это уравнение относительно переменной 
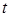, получим
. (6)
Сформулируем метод сопряжённых направлений для минимизации квадратичной функции 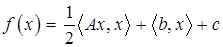, где матрица 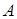положительно определена.
Пусть известны система 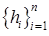векторов взаимосопряжённых относительно матрицы 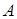и произвольная точка 
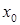из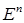 
.
Пусть найдена точка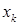 
, 
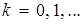Отыщем вектор 
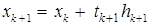, где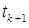 
– полный шаг. Так как для квадратичной функции полный шаг вычисляется по формуле (6), в частности, имеем 
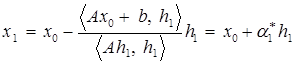. Далее,
.
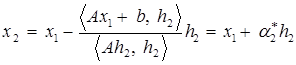Откуда, учитывая формулу для 
, получаем
.
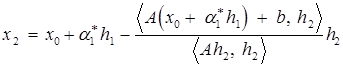С учётом сопряженности векторов 
и 
, получаем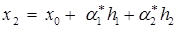 
. Далее методом математической индукции нетрудно получить, что 
для любого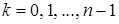 
. Отсюда при 
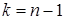получаем 
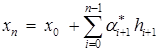. Сравнивая полученную формулу с (3), делаем вывод, что 
.
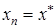Итак, метод сопряженных направлений позволяет найти минимум квадратичной функции не более, чем за итераций.
В рамках изложенной общей схемы метода сопряженных направлений существуют численно реализуемые алгоритмы, различающиеся способом построения системы векторов 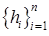взаимосопряженных относительно матрицы 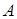. Опишем некоторые способы построения системы векторов взаимосопряженных относительно заданной мат-рицы .
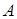Во-первых. Пусть 
– произвольный вектор. Допустим, что уже построены векторы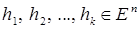 
, 
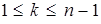, попарно сопряженные относительно матрицы 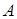. Вектор 
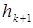определяется как ненулевое частное решение однородной системы линейных алгебраических уравнений
, 
.
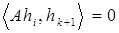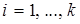Этот способ, несмотря на кажущуюся простоту, на практике не используется в силу больших вычислительных затрат, так как для его реализации требуется решить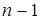 
систему с возрастающим числом уравнений.
Другой подход заключается в следующем. Пусть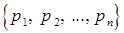 
– некоторая линейно независимая система векторов из 
. Полагаем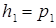 
. Допустим, что уже построены векторы 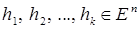, , 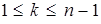попарно сопряженные относительно матрицы 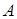. Вектор 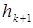находится как линейная комбинация 
, коэффициенты которой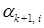 
находятся из требования сопряженности вектора 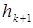и уже найденных векторов 
:
, 
.
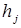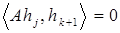Отсюда легко получаем, что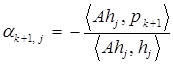 
. Заметим, что этот процесс позволяет строить искомые векторы единственным образом с точностью до множителя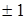 
.
Этот подход также не лишен недостатков, связанных с большим объёмом вычислений, предшествующих применению метода сопряженных направлений.
Основой еще одного подхода является следующее свойство. Допустим, что векторы 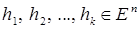, , 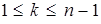попарно сопряжены относительно матрицы 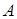. Обозначим через 
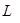линейное подпространство, образованное системой векторов 
. Пусть зафиксированы два вектора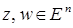 
. Введем линейные многообразия 
, 
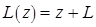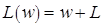. Пусть точк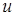и 
и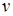 
определяются следующим образом: 
, 
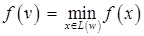, где 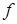– квадратичная функция.
Теорема 2. Пусть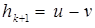 
. Если вектор 
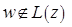, то вектор 
сопряжен относительно матрицы 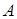с векторами 
.
Теорема 2 позволяет находить взаимосопряженные векторы не до начала работы метода сопряженных направлений, а в процессе его реализации. На этом подходе базируется несколько численных алгоритмов метода.
Однако наиболее эффективной реализацией метода сопряжённых направлений является так называемый метод сопряженных градиентов. В этом методе для нахождения сопряженных направлений последовательно используются элементы градиентного метода..
В заключение отметим, что существуют обобщения метода сопряжённых направлений для минимизации функций, не являющихся квадратичными. В этом случае метод, вообще говоря, не является конечным.
Date: 2015-06-12; view: 1356; Нарушение авторских прав