
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Математическое описание метода
|
|
Допустим, имеется система уравнений ограничений:
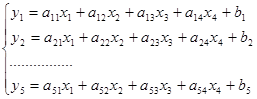
Допустим, требуется вывести из числа свободных переменных какую – либо переменную, например, х 2 и перевести ее в базисную, а в замен ее ввести в число свободных какую то базисную, например у3, т. е. х2 ↔ у3. Если проводить этот процесс математическим способом то, необходимо было бы переразрешать каждое уравнение в системе ограничений относительно новой свободной переменной, т. е. новое получившееся уравнение, в котором была произведена замена необходимо подставить во все остальные уравнения, а так же целевую функцию. Данная процедура является громоздкой, поэтому проще задачу решить с помощью определенного алгоритма и записывать все промежуточные результаты в таблицу. Чтобы этот алгоритм был проще и лучше запоминался необходимо произвести следующие преобразования:

Избавляемся от отрицательных коэффициентов для этого принимаем
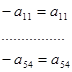
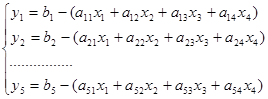
Данная форма записи уравнений называется стандартной.
| СЧ | х1 | х2 | х3 | х4 | |
| у1 | b1 | a11 | a12 | a13 | a14 |
| у2 | b2 | a21 | a22 | a23 | a24 |
| у3 | b3 | a31 | a32 | a33 | a34 |
| у4 | b4 | a41 | a42 | a43 | a44 |
| у5 | b5 | a51 | a52 | a53 | a45 |
При пересечении разрешающей строки у3 и разрешающего столбца х2 получаем разрешающий элемент а32.
Необходимо найти коэффициенты, которые получатся в разрешающей строке после обмена х2 ↔ у3.
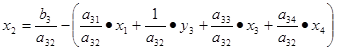
| СЧ | х1 | у3 | х3 | х4 | |
| у1 | 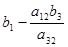
| 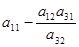
| 
| 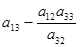
| 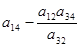
|
| y2 | 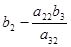
| 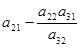
| 
| 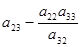
| 
|
| x2 | 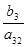
| 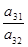
| 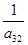
| 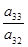
| 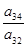
|
| y4 | 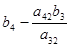
| 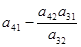
| 
| 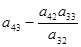
| 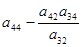
|
| y5 | 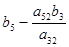
| 
| 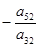
| 
| 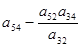
|
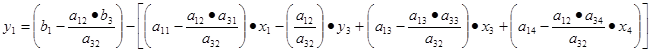
Date: 2015-06-11; view: 437; Нарушение авторских прав