Частинні похідні

Означення 4. Частинний приріст функції z=f(х;y) по x у точці M(x;y) визначається формулою 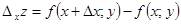. (2.1)

Означення 5. Частинний приріст функції z=f(х;y) по y у точці M(x;y) визначається формулою . (2.2)

Означення 6. Повний приріст функції z=f(x;y) у точці M(x;y) визначається формулою 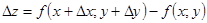. (2.3)

Означення 7. Окіл радіуса r точки M₀(x₀;y₀) – це сукупність усіх точок M(x;y), які задовольняють нерівності 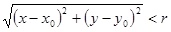, тобто сукупність усіх точок, які лежать на полі круга радіуса r з центром у точці M₀(x₀;y₀).

Нехай функція z=f(x;y) визначена у деякій області D площини xOy і нехай точка M₀(x₀;y₀) 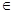D.

Означення 8. Число А називається границею функції f(x;y) при наближенні точки M(x;y) до точки M₀(x₀;y₀), якщо для будь-якого числа 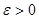можна знайти таке число 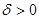( 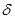залежить від 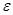), що для всіх точок M(x;y), координати яких задовольняють нерівність 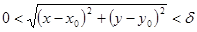, тобто точок M(x;y) із 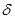– околу точки M₀(x₀;y₀), виконується нерівність

.

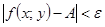Якщо А – границя функції f(х;y) при M(x;y)→ M₀(x₀;y₀), то це записується так:

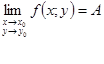. (2.4)

Означення 9. Нехай точка M₀(x₀;y₀) 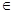D – області визначення функції f(х;y). Функція z=f(х;y) називається неперервною у точці M₀(x₀;y₀), якщо границя функції в ній існує і дорівнює значенню функції в цій точці, тобто

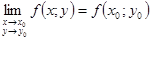, (2.5)

причому точка M(x;y) наближається до точки M₀(x₀;y₀) довільним чином, залишаючись в області визначення функції.

Якщо 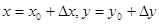, то (2.5) матиме вигляд:

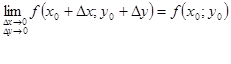(2.6)

або

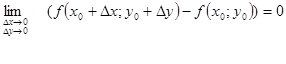. (2.7)

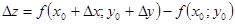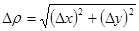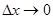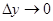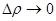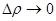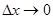Використовуючи формулу (2.3) повного приросту функції z=f(х;y) у точці M₀(x₀;y₀), маємо і, крім того, позначивши (якщо і , тоді і, навпаки, якщо , то і 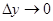), рівність (2.7) запишеться у вигляді:

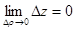. (2.8)

Означення 10. Функція, неперервна у кожній точці деякої області, називається неперервною у цій області.

Означення 11. Точка М₁(х₁;y₁), в якій порушується умова (2.5) неперервності функції z=f(х;y), називається точкою розриву цієї функції.

Приклад 3. Довести, що функція z=x²+y² неперервна у будь-якій точці (х;y) площини xOy.

Ця функція визначена в усіх точках площини xOy. Її повний приріст для будь-яких x, y, ∆x, ∆y має вигляд:

.

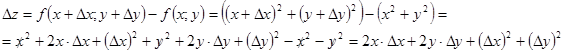Перейшовши до границі, коли 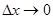і 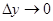, дістанемо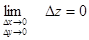

і отже, дана функція неперервна у будь-якій точці (х;y) площини xOy.

Означення 12. Частинною похідною за х функцією двох змінних z=f(х;y) називається границя відношення частинного приросту 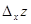до приросту цієї змінної ∆х, якщо приріст змінної ∆х довільним чином прямує до нуля.

Частинна похідна за х для функції z=f(х;y) позначається так:

; .

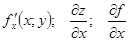За означенням 12

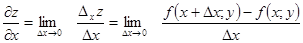. (2.9)

Означення 13. Частинною похідною за y функцією двох змінних z=f(х;y) називається границя відношення частинного приросту 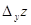до приросту цієї змінної ∆y, якщо приріст змінної ∆y довільним чином прямує до нуля. Позначається така похідна так:

; .

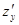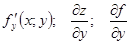За означенням 13

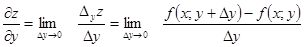. (2.10)

Зауважимо, що 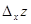обчислюється у припущенні, що y – стала змінна, а 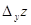– у припущенні, що х – стала змінна. Тому при обчисленні частинних похідних функції двох змінних можна користуватися вже відомими правилами й формулами диференціювання функції однієї змінної, вважаючи при цьому іншу змінну сталою.

Аналогічно, частинні похідні функцій більшого числа змінних визначаються та обчислюються у припущенні, що змінюється лише одна з незалежних змінних, а інші при цьому сталі.

Приклад 4. Знайти частинні похідні функцій:

а) ;

б) ;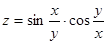

в) ;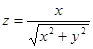

г) .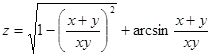

а) Припускаючи, що y стала і застосовуючи правила й формули диференціювання функції однієї змінної х, знаходимо частинну похідну по х:

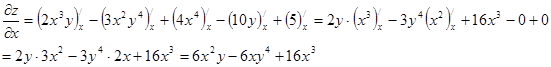
Припускаючи, що х стала і застосовуючи правила й формули диференціювання функції однієї змінної y, знаходимо частинну похідну по y:

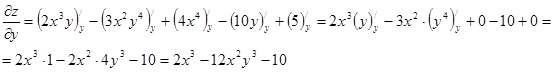
б)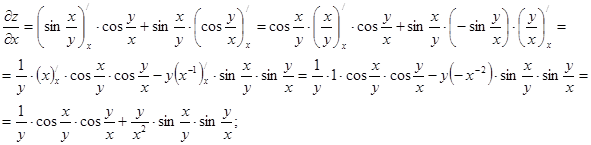

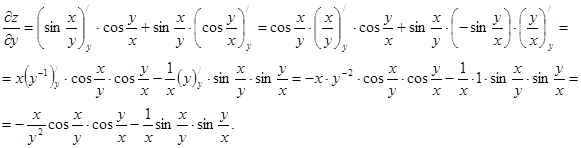
в)

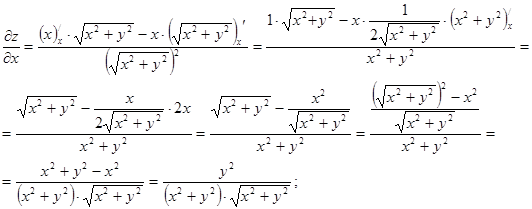
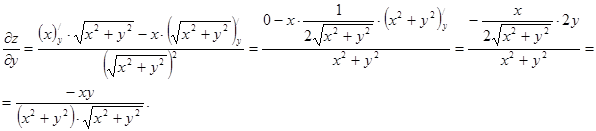г)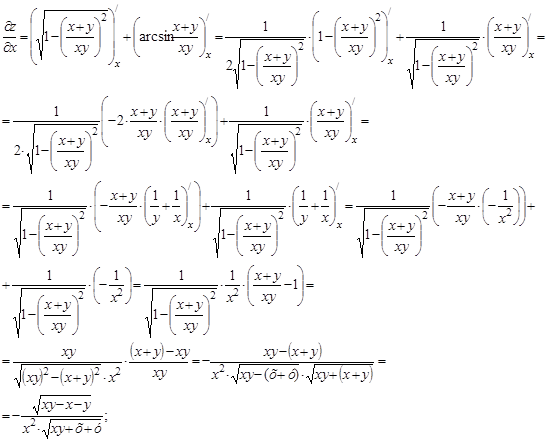

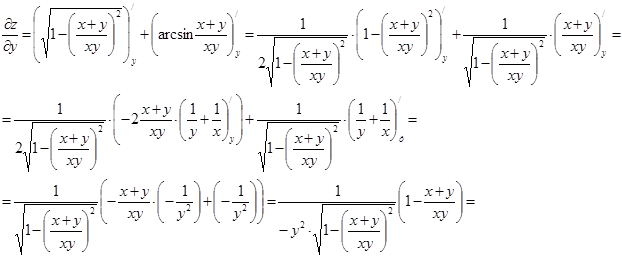
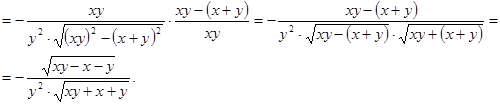
Приклад 5. Довести, що функція 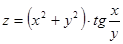задовольняє рівняння .

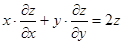Знайдемо спочатку частинні похідн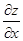і і .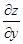

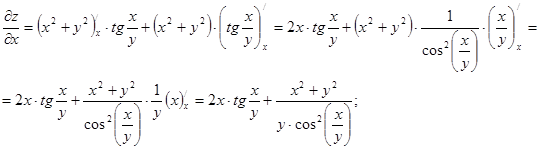
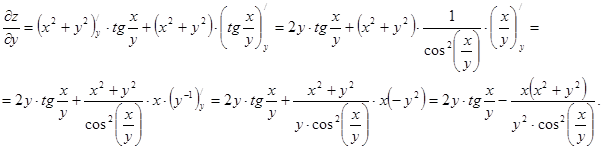
Підставимо вираз для z, 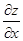і 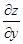у дане рівняння

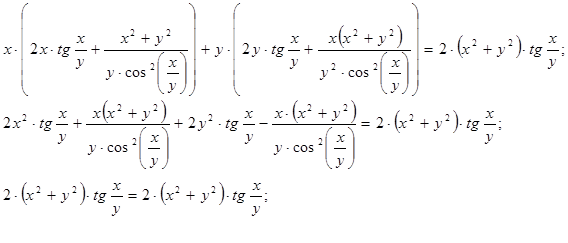
Таким чином, доведено, що дана функція задовольняє дане рівняння.

Date: 2015-06-11; view: 476; Нарушение авторских прав