Авторегрессионное преобразование

Важной проблемой при оценивании регрессии является автокорреляция остатков е, которая говорит об отсутствии первоначально предполагавшейся их взаимной независимости. Автокорреляция остатков первого порядка, выявляемая с помощью статистики Дарбина-Уотсона, говорит о неверной спецификации уравнения либо о наличии неучтенных факторов. Естественно, для её устранения нужно попытаться выбрать более адекватную формулу зависимости, отыскать и включить важные неучтенные факторы или уточнить период оценивания регрессии. В некоторых случаях, однако, это не даст результата, а отклонения е_i просто связаны авторегрессионной зависимостью. Если это авторегрессия первого порядка, то её формула имеет вид е_i= e_i-1 + u_i (коэффициент авторегрессии, |<1), и мы предполагаем, что остатки ui в этой формуле обладают нужными свойствами, в частности - взаимно независимы. Оценив, введем новые переменные у'_i=у_i -y_i-1; x'_i=x_i -x_i-1; (это преобразование называется авторегрессионным (AR), или преобразованием Бокса-Дженкинса). Пусть мы оцениваем первоначально формулу линейной регрессии у_i= а + bx_i + е_i. Тогда

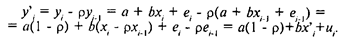
Если величины u_i.действительно обладают нужными свойствами, то в линейной регрессионной зависимости у'_i= а₁ + bx'_i + u_i автокорреляции остатков u_i уже не будет, и статистика DW окажется близкой к двум. Коэффициент b этой формулы принимается для исходной формулы у = а+bх+е непосредственно, а коэффициент а, рассчитывается по формуле.

Оценки коэффициентов а и b нужно сравнить с первоначальными оценками, полученными для расчета отклонений е_i Если эти оценки совпадают, то процесс заканчивается; если нет - то при новых значениях а и b вновь рассчитываются отклонения е до тех пор, пока оценки а и b на двух соседних итерациях не совпадут с требуемой точностью.

В случае, когда остатки «также автокоррелированы, авторегрессионное преобразование может быть применено ещё раз. Это означает использование авторегрессионного преобразования более высокого порядка, которое заключается в оценке коэффициентов авторегрессии соответствующего порядка для отклонений е. и использовании их для построения новых переменных. Такое преобразование вместо AR(1) называется AR(s) - если используется авторегрессия порядка s.

О целесообразности применения авторегрессионного преобразования говорит некоррелированность полученных отклонений u_i,. Однако даже в этом случае истинной причиной первоначальной автокорреляции остатков может быть нелинейность формулы или неучтенный фактор. Мы же, вместо поиска этой причины, ликвидируем её бросающееся в глаза следствие. В этом - основной недостаток метода AR и содержательное ограничение для его применения.

Кроме авторегрессионного преобразования, для устранения автокорреляции остатков и уточнения формулы регрессионной зависимости может использоваться метод скользящих средних (MovingAve-rages, или МА). В этом случае считается, что отклонения от линии регрессии еiописываются как скользящие средние случайных нормально распределенных ошибок е_i предполагается, что

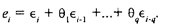(5.1)

Это формула для преобразования МА q-го порядка, или MA(q); МА(1), например, имеет вид е_i = є_i + _iє_i-1. Параметры _i, как и в случае авторегрессионного преобразования, могут оцениваться итерационными методами.

Во многих случаях сочетание методов AR и МА позволяет решить проблему автокорреляции остатков даже при небольших s и q. Еще раз повторим, что адекватным такое решение проблемы является лишь в том случае, если автокорреляция остатков имеет собственные внутренние причины, а не вызвана наличием неучтенных (одного или нескольких) факторов.

Методы AR и МА могут использоваться в сочетании с переходом от объемных величин в модели к приростным, для которых статистическая взаимосвязь может быть более точной и явной. Модель, сочетающая все эти подходы, называется моделью ARIMA (AutoregressiveIntegratedMovingAverages). В общем виде ее формулу можно записать так:

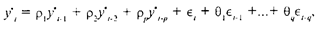(5.2)

где {р^} и {9^} - неизвестные параметры, и е - независимые, одинаково нормально распределенные СВ с нулевым средним. Величины у* представляют собой конечные разности порядка d величин у, а модель обозначается как АRIМА(р,d,q).

Date: 2015-06-11; view: 783; Нарушение авторских прав