Вычисление основных статистических показателей

Главная задача математической статистики заключается в сведе­нии большого объема исходных количественных данных к нескольким математико-статистическим показателям. К ним относятся, прежде всего, простейшие показатели, характеризующие средний уровень и колеблемость (варьирование) исходных данных. Средний уровень опи­сывается с помощью моды, медианы и средней арифметической, а ко­леблемость - размахом, средним абсолютным и средним квадратическим отклонениями, коэффициентом вариации.

Мода - это наиболее часто встречаемое числовое значение при­знака из всех значений элементов изучаемой статистической совокуп­ности. Положительная особенность моды заключается в том, что ее числовое значение не зависит от крайних значений.

Медиана - срединное (центральное) значение признака в ранжи­рованном ряду данных, расположенных в порядке возрастания призна­ка. Проще - это середина ранжированного ряда. Однако в математико-статистических исследованиях наиболее часто и результативно исполь­зуется показатель среднего уровня, названный средним арифметиче­ским. Он служит для краткой, обобщенной характеристики статистиче­ской совокупности по какому-либо признаку. Географу часто приходится вычислять и использовать среднюю температуру воздуха. В статистическом показателе отбрасывается случайное и вскрывается наиболее типичное, существенное, характерное для всей статистической совокупности в целом. Особая ценность средней арифметической за­ключается в том, что она лежит в основе вычисления показателей ко­леблемости признаков, корреляционных зависимостей и других математико-статистических характеристик.

Средняя арифметическая (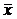) вычисляется по формуле

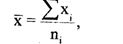
где х_i — отдельные наблюдения; n - число наблюдений.

Проверка правильности вычисления средней арифметической производится путем вычисления центральных отклонений (х_i - 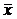), алгебраическая сумма которых теоретически должна равняться нулю.

Роль средних исключительно велика. Они позволяют:

1) оценить значение отдельной величины путем сравнения ее со сред­ней;

2) определить наличие связи между явлениями посредством анализа средних двух или нескольких признаков по одним и тем же территори­ям или временным промежуткам;

3) определить общую тенденцию развития явления.

Положительную роль пространственного и временного осредне­ния в географических исследованиях не следует преувеличивать. Более того, нужно иметь в виду, что средние по слишком крупным территориальным единицам или большим временным промежуткам могут не только сгладить, но и исказить реальную картину размещения и функ­ционирования изучаемых явлений.

Простейшим показателем колеблемости являются лимиты, то есть максимальные и минимальные значения количественных при­знаков статистической совокупности.

Разность между максимальным и минимальным значениями при­знака называют размахом.

В математической статистике отдают предпочтение другому пока­зателю степени колеблемости - среднему квадратическому отклоне­нию, который вычисляется следующим образом. Каждое центральное отклонение возводится в квадрат. Затем находят среднюю арифметиче­скую из этих квадратов и извлекают из нее квадратный корень. Форму­ла среднего квадратического отклонения:

где d (сигма) - знак среднего квадратического отклонения.

В теоретических формулах d часто выступает возведенной в квадрат. Эта величина называется дисперсией. Она также является ме­рой колеблемости признака.

Среднее квадратическое отклонение является размерным показа­телем колеблемости признака. Оно выражается в тех же единицах, что и варианты признака. Поэтому сигма может служить непосредственным показателем колеблемости только тогда, когда сравниваются однород­ные количественные признаки.

Поэтому для сравнения разнородных признаков введен особый показатель - коэффициент вариации (V), представляющий собой от­ношение d к 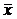. Обычно коэффициент вариации выражается в процен­тах, тогда его формула будет иметь следующий вид:

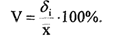
Обратим внимание на то, что коэффициент вариации применим для сравнения колеблемостей только тех количественных показателей, которые не могут принимать отрицательных значений.

Date: 2015-07-17; view: 488; Нарушение авторских прав