Классификация моделей. Одно из достоинств метода модели­рования состоит в возможности построения моделей с «удобной» реализацией

Одно из достоинств метода модели­рования состоит в возможности построения моделей с «удобной» реализацией, ибо удачный выбор реализации делает исследова­ние модели несравненно более легким, чем исследование ориги­нала, и в то же время позволяет сохранить существенные черты его состава, структуры и функционирования.

В зависимости от особенностей изучаемой системы и задач ис­следования применяются самые разнообразные модели, которые целесообразно классифицировать по следующим признакам (рис.).

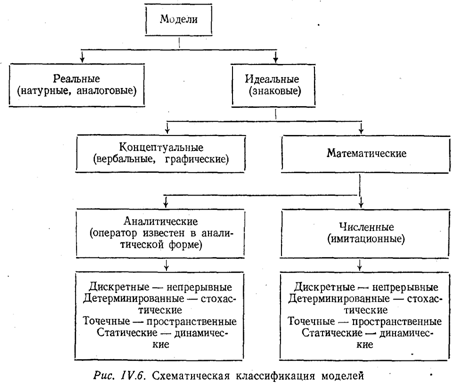
По типу реализации различаются реальные и знаковые моде­ли. Реальная модель отражает существенные черты оригинала уже по самой природе своей физической реализации. Например, аквариум с его растительностью, животным и микробным населением воспроизводит некоторые черты обитаемых природных во­доемов уже потому, что он сам является населенным водоемом, хотя и значительно меньших размеров. В отличие от реальной, знаковая модель представляет собой условное описание системы-оригинала с помощью алфа­вита символов и операций над символами, в результате чего по­лучаются слова и предложения некоторого языка, которые интерпретируются как образы некоторых свойств элементов системы-оригинала и связей между ними. Знаковые модели не­сравненно богаче возможностями, чем реальные, ибо они почти не связаны ограничениями физической реализации.

знаковые модели имеют две разновидности: это, во-первых, так называемые концептуальные и, во-вторых, математические модели.

Концептуальная модель представляет собой несколько более формализованный и систематизированный вариант традиционного естественнонаучного описания изучаемой экосистемы, состоящей из научного текста, сопровождаемого блок-схемой системы, табли­цами, графиками и прочим иллюстративным материалом. Термин «концеп­туальная модель» подчеркивает, что назначение этой модели — служить ясным, обобщенным и в то же время достаточно полным выражением знаний и представлений исследователя об изучаемой системе в рамках и средствами определенной научной концепции например, в рамках «энергетической» или «биогеохимической» концепции.

В зависимости от свойств разрешающего оператора матема­тические модели классифицируются на аналитические и численные. Если для оператора найдено точное ана­литическое выражение, позволяющее для любых входных функ­ций и начальных условий непосредственно определять значение переменных состояния в любой нужный момент, то мо­дель принято называть аналитической. Однако в подавляющем большинстве случаев нахождение аналитического выражения для разрешаю­щего оператора оказывается затруднительным или в принци­пе невозможным. В таком случае нередко удается найти алго­ритм (процедуру) численного решения этих уравнений на ЭВМ, в результате чего получается реализация оператора в виде ма­шинной программы, с помощью которой по входным и начальным данным рассчитываются значения переменных состояний на интервал. Такие модели называются чис­ленными или имитационными.

В зависимости от степени определенности предсказания решения (результата) модели делятся на детер­минированные и стохастические (вероятностные). Если в детер­минированной модели значения переменных состояния опреде­ляются однозначно (с точностью до ошибок вычисления), то стохастическая модель для каждой переменной дает распределение возможных значений, характеризуемое та­кими вероятностными показателями, как математическое ожида­ние, среднее квадратическое отклонение и т. п.

По характеру временного описания динамики переменных со­стояния различаются дискретные и непрерывные модели. Дис­кретная модель описывает поведение системы на фиксированной последовательности моментов времени, тогда как в непрерывной модели значения переменных состояния могут быть рассчитаны для любой точки рассматриваемого интервала.

Следующий важный признак, по. которому различаются мате­матические модели, — это характер описания их про­странственного строения. Моде­ли, в которых пространственное строение экосистемы не рассмат­ривается, т. е. в качестве пере­менных состояния фигурируют зависящие только от времени пе­ременные, принято называть моделями с сосредо­точенными значениями (или точечными моделями), в отличие от моделей с распределенными значениями, в которых переменные состояния зависят не только от времени, но и от пространствен­ных координат (одной или нескольких).

Date: 2015-07-17; view: 590; Нарушение авторских прав