
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Абстрактные конечные автоматы 1-го и 2-го рода. Матрицы переходов и выходов. Представление графом
|
|
Абстрактный автомат задается как совокупность шести объектов:
- множества входных сигналов Х (входной алфавит автомата);
- множества выходных сигналов Y (выходной алфавит автомата);
- множества состояний автомата А;
- элемента а0 Î А, называемого начальным состоянием автомата;
- функций переходов j(а,x) и выходов y(а,x), задающих однозначные отображения множества (а,x), где а Î А и x Î X, в множества А и Y.
Закон функционирования автомата первого рода задается уравнениями вида:
| а(t)= j[а(t-1), x(t)]; y(t)=y[а(t-1), x(t)]; t=1,2,...; | (7) |
Закон функционирования автомата второго рода:
| а(t)= j[а(t-1), x(t)]; y(t)=y[а(t), x(t)]; t=1,2,... | (8) |
В практике используют:
- автомат Мили: произвольный конечный автомат первого рода;
- автомат Мура: частный случай конечных автоматов второго рода, у которого функция выходов y(а,x) не зависит от переменной х.
Автомат называется конечным если конечно число его состояний. Автоматы задают табличным способом или направленным графом. В первом случае строят матрицы переходов и выходов. Строки обеих этих таблиц обозначаются входными сигналами автомата, а столбцы – его состояниями. На пересечении строки и столбца таблицы переходов ставится соответствующее значение функции переходов j(а,x), а в таблице выходов – значение y(а,x). Для автомата Мура сдвинутая таблица выходов сводится к одной строке, поэтому часто в таблице переходов над каждым состоянием аi автомата, обозначающим тот или иной столбец таблицы, ставят соответствующий этому состоянию выходной сигнал j (аi,x) = y(аi).
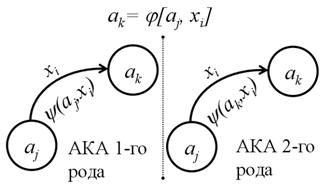
При задании автомата с использованием направленного графа вершины графа отождествляются с состояниями автомата, а стрелки – с выходными сигналами. Если входной сигнал xi вызывает переход автомата из состояния аj в состояние аk, то на графе автомата этому сигналу соответствует помеченная буквой xi стрелка, соединяющая вершину, соответствующую состоянию аj, с вершиной, соответствующей состоянию аk. Для задания функции выхода ребра графа также помечаются соответствующими выходными сигналами. Если обозначенная входным сигналом xi стрелка соединяет вершину аj с аk, то в случае автоматов первого рода ей предписывается выходной сигнал y(аj,xi), а в случае автоматов второго рода – выходной сигнал y(аk,xi) (см. рис. 12).
 |
Date: 2015-07-17; view: 1025; Нарушение авторских прав