Задача идентификации. Результатом решения задачи идентификации является имитационная или аналитическая модель структурного примитива

Результатом решения задачи идентификации является имитационная или аналитическая модель структурного примитива. Как уже отмечалось, аналитические модели делятся на теоретические и экспериментальные. Теоретические модели получают на основе известных описаний процессов функционирования объекта. Экспериментальные – на основе изучения поведения объекта моделирования во внешней среде.

Для построения экспериментальных моделей используют:

- методы аппроксимация зависимостей;

- методы корреляционного и регрессионного анализа;

- методы планирования эксперимента.

Пусть экспериментальная статистика функционирования структурного примитива задана таблично. В этом случае значения функции базисной координаты известны только для дискретных значений входной переменной. Для того чтобы вычислять значение базисной координаты в любой произвольной точке, необходимо восстановить непрерывную функцию v=f(х). Такое приближение называют аппроксимацией.

Аппроксимация характеристик структурных примитивов применяется в следующих случаях:

- если аналитическое описание характеристики неизвестно и она задана набором экспериментальных данных;

- аналитическое описание v=f(х) сложное и затрудняет расчеты.

Постановка задачи аппроксимации имеет два варианта. В первом случае осуществляется поиск аппроксимирующей функции, наилучшим образом описывающей экспериментальную статистику, при условии обязательного прохождения графика аппроксимирующей функции через определенные заданные точки экспериментальной статистики (см. рис. 8-а). Эти точки называются узлами. Второй вариант постановки задачи аппроксимации не имеет ограничивающего условия обязательного прохождения функции через узлы (см. рис. 8-б).

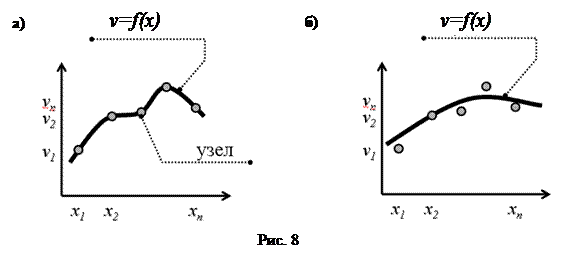
Для решения первой задачи используется методы кусочно-линейной аппроксимации и аппроксимации сплайнами.

Кусочно-линейная аппроксимация получается соединением узлов отрезками прямых линий. Узлы располагаются так, чтобы обеспечить наименьшую ошибку между аппроксимирующей и точной функцией.

Чаще используют аппроксимацию сплайнами. В отличие от интерполяции полиномом, которым описывается вся область данных, при интерполяции сплайнами строится отдельный полином, описывающий интервал от узла x_i-1 до узла x_i (см. рис. 9).

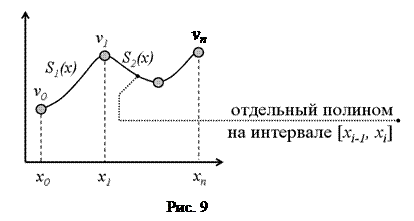
Наиболее часто используют полиномы третьей степени – кубические сплайны. На каждом отрезке 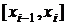кубический сплайн 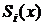является многочленом третьей степени:

.

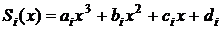В узлах 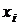сплайн 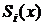принимает заданные значения , :

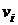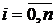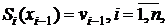
	(1)
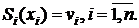
	(2)

Условия (1) и (2) требуют, чтобы сплайны соприкасались в заданных точках. Количество условий таких условий равно 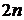. Во внутренних узлах 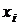, 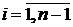сплайн имеет непрерывную первую и вторую производные:

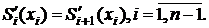
	(3)
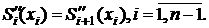
	(4)

Условия (3) и (4) означают, что в местах соприкосновения сплайнов их первые и вторые производные должны быть равны. Таких условий 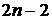. Для отыскания искомого сплайна требуется найти коэффициенты 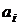, , 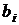, 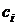многочленов 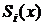, , 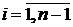т. е. 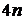неизвестных. Однако количество уравнений, записанных по условиям (1)–(4) равно 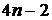. Чтобы система алгебраических уравнений имела решение, необходимо, чтобы число уравнений равнялось числу неизвестных. Следовательно, для разрешимости задачи нужны еще два дополнительных условия. Их обычно получают из естественного предположения о нулевой кривизне графика сплайна на концах:

, .

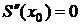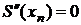Полученный таким образом сплайн называют естественным. Если есть дополнительные сведения о поведении функции на концах интервала интерполяции, то можно записать другие краевые условия.

Date: 2015-07-17; view: 514; Нарушение авторских прав