Вопрос 5. Формальная модель объекта

Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:

совокупность входных воздействий на систему

;

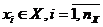совокупность воздействий внешней среды

;

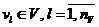совокупность внутренних (собственных) параметров системы

;

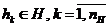совокупность выходных характеристик системы

.

При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.

При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми переменными, которые в векторной форме имеют соответственно вид

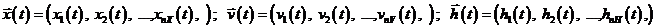
Выходные характеристики системы являются зависимыми переменными и в векторной форме имеют вид .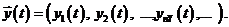

Процесс функционирования системы S описывается во времени оператором F_s, который в общем случае преобразует независимые переменные в зависимые в соответствии с соотношениями вида

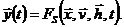(5.1)

Совокупность зависимостей выходных характеристик системы от времени y_j(t) для всех видов 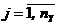называется выходной траекторией . Зависимость (5.1) называется законом функционирования системы S и обозначается F_s. В общем случае закон функционирования системы F_s может быт задан в виде функции, функционала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.

Весьма важным для описания и исследования системы S является понятие алгоритма функционирования A_s, под которым понимается метод получения выходных характеристик с учетом входных воздействий 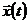, воздействий внешней среды 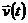и собственных параметров системы 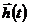. Очевидно, что один и тот же закон функционирования F_s системы S может быть реализован различными способами, т. е. с помощью множества различных алгоритмов функционирования A_s.

Соотношения (5.1) являются математическим описанием поведения объекта (системы) моделирования во времени t, т. е. отражают его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями (системами).

Для статических моделей математическая модель (5.1) представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и {X, V, Н}, что в векторной форме может быть записано как

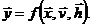(5.2)

Соотношения (5.1) и (5.2) могут быть заданы различными способами: аналитически (с помощью формул), графически, таблично и т. д.

Такие соотношения в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые состояниями.

Состояние системы S характеризуется векторами

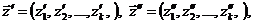
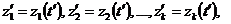
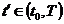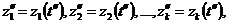
Где в момент , в момент .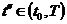

Если рассматривать процесс функционирования системы S как последовательную смену состояний z₁(t), z₂(t),..., z_k(t), то они могут быть интерпретированы как координаты точки в k -мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний 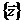называется пространством состояний объекта моделирования Z, причем z_k Î Z.

Состояния системы S в момент времени t₀<t^*≤Т полностью определяются начальными условиями 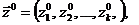входными воздействиями 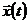, внутренними параметрами 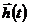и воздействиями внешней среды 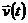, которые имели место за промежуток времени t* - t₀, с помощью двух векторных уравнений

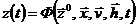; (5,3)

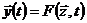. (5.4)

Первое уравнение по начальному состоянию 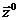и независимым переменным 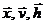определяет вектор-функцию 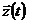, а второе по полученному значению состояний 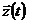- зависимыми переменные на выходе системы . Таким образом, цепочка уравнений объекта «вход — состояния — выход» позволяет определить характеристики системы

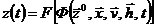(5.5)

В общем случае время в модели системы S может рассматриваться на интервале моделирования (0, Т) как непрерывное, так и дискретное, т. е. квантованное на отрезки длиной Dt временных единиц каждый.

Таким образом, под математической моделью объекта (реальной системы) понимают конечное подмножество переменных 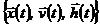вместе с математическими связями между ними и характеристиками .

Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, т. е. если можно считать, что в этом случае стохастические воздействия внешней среды 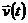и стохастические внутренние параметры 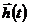отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

(5.6)

Очевидно, что детерминированная модель является частным случаем стохастической модели.

Date: 2015-07-17; view: 638; Нарушение авторских прав