Разработка марковской модели системы с дискретным временем

n кодирование состояний случайного процесса;

n построение размеченного графа переходов;

n формирование матрицы интенсивностей переходов;

n составление системы линейных алгебраических уравнений.

9. Примеры моделей на основе марковских цепей и процессов. Эргодическое свойство.

Рассмотрим развитие некоторой популяции, особи которой могутрождаться и умирать. Положим, что при наличии i особей в популяциирождение новых особей происходит с интенсивностью лямбда-итоеи с интенсивностью мю-итое – особи умирают. Пусть в любой момент времени можетпроисходить рождение или гибель только одной особи, и интервалывремени между двумя моментами рождения и гибели распределены поэкспоненциальному закону с параметрами лямбда-итоеи мю-итое соответственно. Тогдапроцесс "гибели и размножения" может быть представлен марковскимслучайным процессом с непрерывным временем (рис.5.1,а), в которомсостояние E i соответствует наличию i особей в популяции (i =0, 1, …),причем число состояний может быть конечным или бесконечным.Отметим, что состояние E 0 соответствует вырождению популяции.

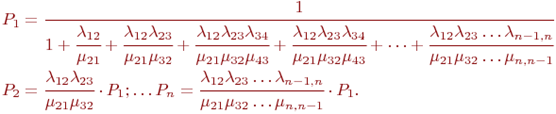
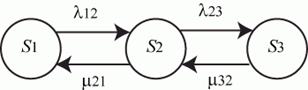
надёжность системы из двух компьютеров

t – среднее время работы без отказов,
t_р – среднее время восстановления

l₁₂ = 2 × 1/t, l₂₃ = 1/t

m₂₁ = 1/t_р, m₃₂ = 2 × 1/t_р

Стационарные вероятности:

P₁ = 1/ (1+ 2 × t_р /t + t_р²_//t²)

P₂ = 2 × t_р /t ×P₁

Date: 2015-07-17; view: 460; Нарушение авторских прав