Устойчивость

3. чувстви­тельность.

Адекватность модели - степень соот­ветствия модели тому реальному объекту или процессу, для описания которого она строится или целям исследования.

Процедура оценки адекватности модели реально существующей си­стеме основана на сравнении результатов измерений характеристик на реальной системе с результатами экспериментов на модели. Такая оцен­ка может проводиться различными способами:

1. по средним значениям отклика модели и реальной системы;

2. по дисперсиям отклонений откли­ков модели от среднего значения откликов системы;

3. по максимальному значению относительных отклонений отклика модели от отклика реаль­ной системы.

Указанные способы весьма близки между собой, поэтому для иллюстрации описываемого подхода к оценке адекватности модели рассмотрим первый способ.

При этом способе проверяется гипотеза о близости среднего значе­ния переменной Y среднему значению отклика реальной системы Y*. В результате N опытов на реальной системе получают множество значе­ний (выборку) Y*. Выполнив М экспериментов на модели, также полу­чают выборку значений наблюдаемой переменной Y. Затем вычисляют значения математического ожидания и дисперсии откликов модели и реальной системы, после чего выдвигается гипотеза о близости сред­них величин Y и Y* в статистическом смысле. Основой для проверки гипотезы является t-статистика (распределение Стьюдента), ее значе­ние, вычисленное по результатам испытаний, сравнивается с критичес­ким значением t, взятым из справочной таблицы. Если выполняется неравенство t < t_кр, то гипотеза принимается.

Статистические методы применимы только в том случае, если оценивается адекватность модели существу­ющей системе. Для проектируемой системы в качестве эталонного объекта принять концептуальную модель проектируемой системы. Тогда оцен­ка адекватности программно реализованной модели заключается в про­верке того, насколько она отражает концептуальную модель.

Устойчивость модели - это ее способность сохранять адек­ватность при исследовании эффективности системы на всем возмож­ном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы.

Устойчивость результатов моделирования может быть оценена методами математической статистики. Для этого проверяют гипо­тезу об устойчивости результатов моделирования на основе критерия Уилкоксона: относятся ли две выборки к одной и той же генеральной сово­купности (т.е. обладают ли они одним и тем же статистическим призна­ком).

При статистической оценке устойчивости модели соответствую­щая гипотеза может быть сформулирована следующим образом: при изменении рабочей нагрузки или структуры имитационной модели за­кон распределения результатов моделирования остается неизменным.

Чувствительность модели к изменениям параметров рабочей нагруз­ки и внутренних параметров самой системы оценивают на основе специальных процедур по каждому параметру X_k в отдельнос­ти. Данные, полученные при оценке чувствительности модели, могут быть использованы, в частности, при планировании экспериментов: большее внимание должно уделяться тем параметрам, по которым мо­дель является более чувствительной.

Если в результате проведенной оценки качества модели оказалось, что ее целевые свойства не удовлетворяют разработчика, необходимо выполнить ее калибровку, то есть корректировку с целью приведения модели в соответствие предъявляемым требованиям.

Процесс калибровки модели обычно является итерационным и со­стоит из трех основных этапов:

1. глобальные изменения модели (например, введение в рассмотрение новых процессов, изменение типов событий и т.п.);

2. локальные изменения модели (например, изменение некоторых законов распределения моделируемых случайных величин);

3. изменение специальных параметров, называемых калибровочными.

V Этап: планирование модельных экспериментов

Цели:

1. сокращение общего объема испытаний при соблюдении требова­ний к достоверности и точности их результатов;

2. повышение информа­тивности каждого эксперимента в отдельности.

Поиск плана эксперимента производится в так называемом факторном пространстве. Факторное пространство - это множество внешних и внут­ренних параметров модели, значения которых исследователь может кон­тролировать в ходе подготовки и проведения модельного эксперимента.

Поскольку факторы могут носить как количественный, так и качест­венный характер, значения факторов в теории планирования экспери­ментов обычно называют уровнями.

Если при проведении экспериментов исследователь может изменять уровни факторов, эксперимент называется активным, в противном слу­чае — пассивным.

Обычно план эксперимента строится относительно одного выход­ного скалярного параметра, который называется наблюдаемой перемен­ной. Если моделирование используется как инструмент принятия реше­ния, то в роли наблюдаемой переменной выступает показатель эффек­тивности моделируемой системы.

Существует два основных варианта постановки задачи планирова­ния эксперимента с имитационной моделью:

1. выбрать план эксперимента из всех допустимых, реализация кото­рого при фиксированном числе опытов с моделью даст наиболее досто­верную информацию о функции отклика системы:

2. выбрать допустимый план, при реализации которого статистическая оценка функции отклика может быть получена с заданной точностью при минимальном объеме испытаний.

Решение задачи в первой постановке называется стратегическим пла­нированием эксперимента, а во второй - тактическим планированием.

Цель методов стратегического планирования экспериментов с ими­тационными моделями состоит в получении максимального объема ин­формации об исследуемой системе в каждом испытании модели. Стра­тегическое планирование позволяет ответить на вопрос, при каком со­четании уровней внешних и внутренних факторов может быть получе­на наиболее полная и достоверная информация о поведении исследуе­мой системы.

В процессе стратегического планирования должны быть решены следующие основные задачи:

1. идентификация факторов;

2. выбор уровней факторов;

3. определение набора сочетаний уровней факторов, при которых будут проводиться испытания модели.

Идентификация факторов - их ранжирование по сте­пени влияния на значение наблюдаемой переменной.

По итогам иден­тификации все факторы делят на первичные и вто­ричные.

Первичные – это факторы, в исследовании влияния которых эксперимента­тор заинтересован непосредственно,

Вторичные факторы –факторы, которые не являясь предметом исследования, в то же время оказывают существенное влия­ние на значение наблюдаемой переменной, которым нельзя пренебречь.

Минимальное количество уровней любого фактора равно двум - нижняя и верхняя границы интервала изменения значений фактора. При использовании всего двух уровней можно определить только линейные эффекты. Для учета квадратичных эффектов необходимо рассматривать три уровня фактора, для зависимостей третьего порядка - четыре уров­ня и т.д. Анализ значительно упрощается, если брать только равноот­стоящие друг от друга значения уровней. В этом случае имеет место так называемое ортогональное разбиение уровней.

Выбор уровней факторов производится с учетом двух требований:

1. уровни каждого фактора должны перекрывать весь возможный диапа­зон его изменения:

2. общее количество уровней по всем факторам не долж­но приводить к чрезмерному объему испытаний модели.

Тактическое планирование экспериментов - совокупность методов установления необходимого объема испыта­ний.

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.

Применение полного факторного плана вместо классической схемы, согласно которой каждый раз изменяется только один фактор, имеет следующие преимущества:

1. более полная картина влияния каждого фактора

2. облегчение предсказания отклика, который может быть получен при определенной комбинации условий;

3. если эффекты, обусловленные каждым фактором, статистически независимы, то о влиянии каждого фактора на отклик системы можно получить не меньше информации, чем при изменении в экспериментах только одного фактора при фиксации остальных;

4. если влияние различных факторов на отклик системы не является независимым, а эффекты такого влияния в большей или меньшей степени коррелированны, то в этом случае только полный факторный эксперимент может дать необходимую информацию о взаимодействии факторов.

В общем случае объект исследования можно представить как некий «черный ящик», на входе которого действуют управляющие параметры или, другими словами, факторы x_i. (i = 1, 2,..., n) и некоторые возмуще­ния z_j. (j = 1,2,..., k). На выходе объекта наблюдаются какие-либо харак­теристики объекта y_l (l = 1,2,.... m), например, показатель эффективно­сти исследуемой системы.

На математическом языке задача установления взаимосвязи входных и выходных переменных в исследуемой системе формулируется следу­ющим образом: следует определить функцию отклика

y = f(x_i,x₂,...,x_n)

где у — интересующая исследователя выходная переменная;

x₁, х₂,..., x_n — независимые переменные, которые можно варьировать при проведении эксперимента (факторы).

Во многих случаях цель имитационного моделирования заключает­ся в поиске таких величин независимых переменных, при которых от­клик достигает экстремального значения.

Если все рассматриваемые в задаче поиска оптимума факторы явля­ются дискретными величинами, то задачу можно решить полным пере­бором всех возможных комбинаций значений факторов.

В общем случае функция отклика неизвестна, то ее аппрок­симируют некоторой гладкой функцией, в качестве которой обычно ис­пользуют полином первого или второго порядка.

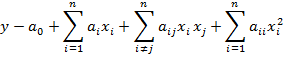
Параметры a₀, a₁..., a_n... — коэффициенты регрессии — оценивают по результатам факторного эксперимента.

Решение задачи поиска оптимальных параметров исследуемой сис­темы на основе имитационных экспериментов осуществляется в несколь­ко этапов:

1. планирование эксперимента;

2. проведение экспериментов и построение по их результатам уравнения регрессии для функции отклика;

3. поиск экстремальных значений факторов, например, методом наискорейшего спуска.

На началь­ном этапе исследования проводят предварительное отсеивание факторов, так как с ростом числа факторов и их уровней количество возмож­ных комбинаций уровней факторов быстро растет. В этом случае сначала строит­ся план отсеивающего эксперимента, реализация которого позволяет сократить число факторов, рассматриваемых в оптимизирующем экс­перименте.

На этапе проведения отсеивающего эксперимента можно рассмат­ривают меньшее число уровней для каждого фактора, чем в оптимизиру­ющем эксперименте. Недостатком полного факторного эксперимента являются значитель­ные затраты времени на его проведение.

Использование полного факторного эксперимента целесообразно в тех случаях, когда в имита­ционных экспериментах исследуется взаимное влияние всех факторов, фигурирующих в модели.

Если взаимодействие факторов отсутствует, или эффектом взаимо­действия факторов можно пренебречь, то проводят частичный фактор­ный эксперимент.

На практике применяются различные варианты построения планов частичных факторных экспериментов:

1. рандомизированный план, предполагающий выбор сочетания уровней факторов для каждого прогона модели случайным образом.

2. латинский план, используется в том случае, когда проводятся экспе­рименты с одним первичным фактором и несколькими вторичными

3. дробный факторный план, в котором для каждого фактора рассмат­риваются всего два уровня - нижний и верхний.

4. эксперименты с изменением факторов по одному. Такой план обеспечивает исследование эффектов от изменения каждого фактора в отдельности.

Для определения необходимого число прогонов модели используют соотношение:

,

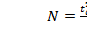Где σ² – дисперсия, t_α – t-критерий для уровня значимости α. έ² – точность оценки определения параметров.

Поскольку дисперсия оцениваемой случайной величины в общем слу­чае неизвестна, необходимо провести 50-100 испытаний и оценить σ², а потом определить необходимое число прогонов модели для каждого «пункта» стратегического плана.

VI Этап: реализация плана экспериментов

На этом этапе от исследователя требуется осуществлять многократные прогоны имитационной модели при различных комбинациях значений управляе­мых параметров модели в соответствии с планом эксперимента, разра­ботанным на этапе планирования эксперимента. При этом необходимо протоколировать результаты каждого прогона модели для их последую­щего анализа и выработки практических рекомендаций.

Основные проблемы, возникающие при эксперименти­ровании с имитационными моделями.

1. Задание начальных условий эксперимента. Необходимо учитывать смещения в статистические оценки параметров отклика модели при переходном периоде. Чтобы уменьшить влияние переходного режима рабо­ты модели на конечные результаты эксперимента, можно поступать сле­дующим образом:

1. запускать модель с модальных (наиболее вероятных) значений установившегося режима работы модели;

2. запускать модель со средних значений установившегося режима работы модели.

2. Выбор «правила остано­ва», определяющего длительность прогона имитационной модели. От про­должительности прогона зависит точность результатов моделирования.

3. Анализ состояния модели в момент прекращения прогона. Учет незавершенных про­цессов может привести к смещению оценки характеристик модели в большую сторону.

4. Определение длитель­ности прогона модели при наличии в модели процессов с разными ско­ростями протекания. Оценку точности результатов моделирования обыч­но выполняют для самого медленного процесса в модели. При разработке имитационной модели обычно выбирают сте­пень детализации модели такой, чтобы скорости протекающих в ней про­цессов не различались более, чем на два порядка. В случаях моделирова­ния редких событий (медленных процессов), например, отказов оборудо­вания, необходимо укрупнять состояния для быстрых процессов.

Date: 2015-07-17; view: 465; Нарушение авторских прав