
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

О роли лоренцевой калибровки в уравнениях электродинамики
|
|
Потенциалы электромагнитного поля.
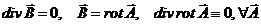 (1)
(1)
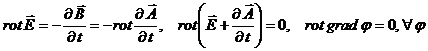 (2)
(2)
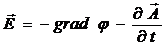 (3)
(3)
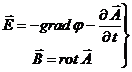 (4)
(4)
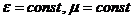
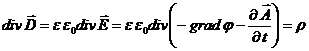 (5)
(5)
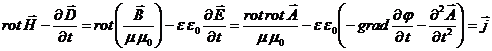 (6)
(6)
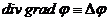
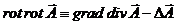 (7)
(7)
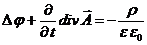 (8)
(8)
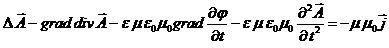 (9)
(9)
потребуем (пока формально)
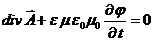 (10)
(10)
результат
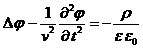 (11)
(11)
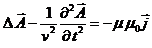 (12)
(12)
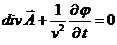 (13)
(13)
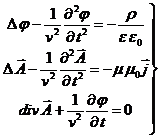 (14)
(14)
Градиентная инвариантность потенциалов электромагнитного поля.
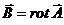
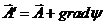 (15)
(15)
 (16)
(16)
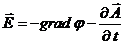 (17)
(17)
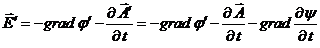 (18)
(18)
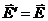 (19)
(19)
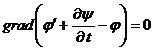
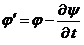 (20)
(20)
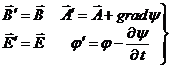 (21)
(21)
пример использования градиентной инвариантности
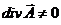
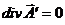 (22)
(22)
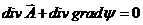 (23)
(23)
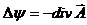 (24)
(24)
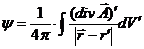 (25)
(25)
пример Калибровка Лоренца

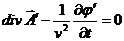 (26)
(26)
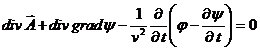 (27)
(27)
 (28)
(28)
О роли лоренцевой калибровки в уравнениях электродинамики
Рассмотрим систему уравнений Максвелла в дифференциальной форме для безграничной непроводящей, однородной и изотропной среды в отсутствие сторонних электрических зарядов с линейными материальными уравнениями 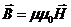 и
и 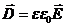 , для которых относительная диэлектрическая e и магнитная проницаемость m не меняется с течением времени. При соблюдении вышеперечисленных условий система уравнений Максвелла имеет вид:
, для которых относительная диэлектрическая e и магнитная проницаемость m не меняется с течением времени. При соблюдении вышеперечисленных условий система уравнений Максвелла имеет вид:
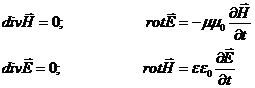 . (29)
. (29)
Выше была показана возможность сведения системы уравнений (29) к двум волновым уравнениям отдельно для вектора напряжённости электрического поля и вектора напряжённости магнитного поля, решения которых можно искать или в форме плоских гармонических бегущих волн или в форме бегущих волн Даламбера. Существование единой электромагнитной волны, поперечность этой волны, ортогональность и синфазность векторов 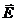 и
и  в произвольной электромагнитной волне, связь между амплитудами волн
в произвольной электромагнитной волне, связь между амплитудами волн 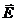 и
и  , ориентацию тройки векторов
, ориентацию тройки векторов 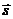 ,
, 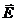 ,
,  , где
, где 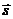 – единичный вектор, задающий направление распространения волны – следствие исходной системы уравнений Максвелла (29).
– единичный вектор, задающий направление распространения волны – следствие исходной системы уравнений Максвелла (29).
Если лоренцева калибровка потенциалов электромагнитного поля имеет место, справедливы уравнения:
ÿ 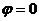 ; (30)
; (30)
ÿ  . (31)
. (31)
В учебной и научной литературе условию калибровки часто отводится чисто вспомогательная роль инвариантного преобразования, позволяющего записать систему уравнений потенциалов электромагнитного поля в более простом виде, и, главное, в форме независимых друг от друга уравнений для скалярного j и векторного 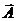 потенциалов отдельно [1,2]. На самом деле роль условия калибровки значительно глубже. Согласно логике вывода уравнений (30) и (31), условие лоренцевой калибровки равноправно с уравнениями Даламбера и представляет собой замыкающую часть единой системы. В этих условиях не приходится говорить о независимости друг от друга скалярного и векторного потенциалов. Аналогичные проблемы обсуждаются в работе [3].
потенциалов отдельно [1,2]. На самом деле роль условия калибровки значительно глубже. Согласно логике вывода уравнений (30) и (31), условие лоренцевой калибровки равноправно с уравнениями Даламбера и представляет собой замыкающую часть единой системы. В этих условиях не приходится говорить о независимости друг от друга скалярного и векторного потенциалов. Аналогичные проблемы обсуждаются в работе [3].
Рассмотрим систему уравнений (30), (31). Уравнения (30) и (31) допускают решения в форме Даламбера:
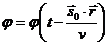 ;
; 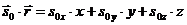 (32)
(32)
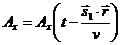 ;
; 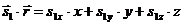 (33)
(33)
 ;
; 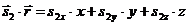 (34)
(34)
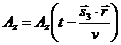 ;
; 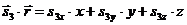 (35)
(35)
векторы 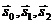 и
и 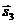 –единичные векторы, задающие направления распространения соответствующих волн,
–единичные векторы, задающие направления распространения соответствующих волн,  -фазовая скорость рассматриваемых волн.
-фазовая скорость рассматриваемых волн.
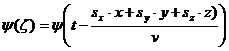 (36)
(36)
□ 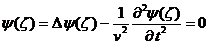 (37)
(37)
 ,
, 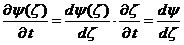 (39)
(39)
□ 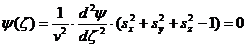 (40)
(40)
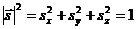 (41)
(41)
□ 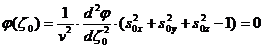 (42)
(42)
□ 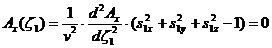 (43)
(43)
□ 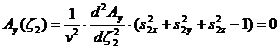 (44)
(44)
□ 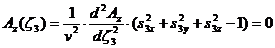 (45)
(45)
Уравнения Даламбера – решение возможно в форме произвольных плоских волн Даламбера для скалярного потенциала и каждой компоненты векторного потенциала, при этом фазовая скорость одна и та же, а направления могут разные.
Требуем выполнения условия калибровки Лоренца
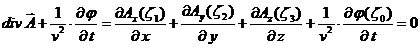 (46)
(46)
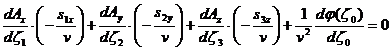 (47)
(47)
В уравнении (47) присутствуют 4 разных функции, каждая из которых зависит от "своего" специфического аргумента. Это уравнение должно быть выполнено в произвольной точке пространства и в любой момент времени. Единственная возможность решения этой проблемы - это потребовать, чтобы аргументы всех функций, входящих в уравнение (47) были одинаковы:
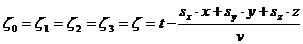 (48)
(48)
В результате оказывается, что обеспечено одно единственное направление распространения волн для компонент векторного потенциала 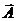 и скалярного потенциала
и скалярного потенциала 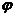 , второй результат - рассматриваемые волны синфазны.
, второй результат - рассматриваемые волны синфазны.
Заготовим выражения для последующего вычисления напряжённостей Е и Н
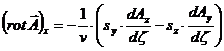 (49)
(49)
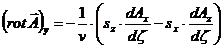 (50)
(50)
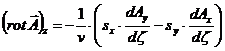 (51)
(51)
градиент 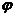
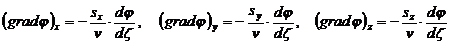 (52)
(52)
производная от А по времени
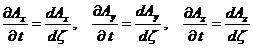 (53)
(53)
компоненты напряжённостей 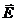 и
и 
 (54)
(54)
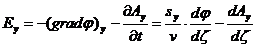 (55)
(55)
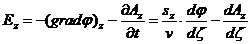 (56)
(56)
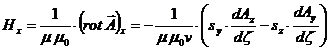 (57)
(57)
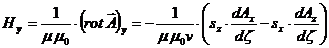 (58)
(58)
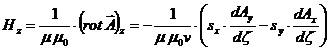 (59)
(59)
ортогональность 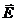 и
и  (непосредственное вычисление)
(непосредственное вычисление)
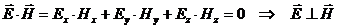 (60)
(60)
ортогональность 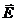 и
и 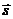
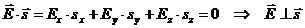 (61)
(61)
(с учётом калибровки Лоренца);
ортогональность  и
и 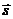 (непосредственное вычисление)
(непосредственное вычисление)
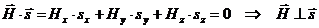 (62)
(62)
Ввыод: рассматриваемая волна поперечная.
Вектор Пойнтинга (окончательные выражения получены с учётом условия s=1, проекции векторов 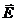 и
и  - действительные величины)
- действительные величины)
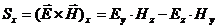 (63)
(63)
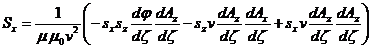 (64)
(64)
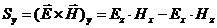 (65)
(65)
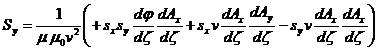 (66)
(66)
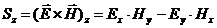 (67)
(67)
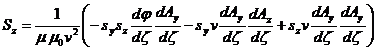 (68)
(68)
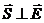 и
и 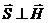 - это очевидно (по построению)
- это очевидно (по построению)
вектор 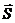 сонаправлен вектору
сонаправлен вектору 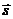 , а это надо показать
, а это надо показать
 (69)
(69)
прямое вычисление (с учётом калибровки Лоренца)
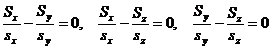 (70)
(70)
Вектор Пойнтинга (мгновенное значение) и единичный вектор направления распространения волны одинаково направлены.
Соотношение между «амплитудами». Из уравнения калибровки Лоренца (непосредственно)
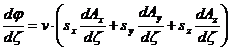 (71)
(71)
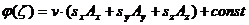 (72)
(72)
Итог:
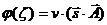 (73)
(73)
Специальный случай:
 (74)
(74)
Вывод: условие лоренцевой калибровки (10) сужает множество допустимых решений совокупности уравнений ÿ 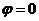 и ÿ
и ÿ  до множества, эквивалентного решениям исходной системы уравнений Максвелла.
до множества, эквивалентного решениям исходной системы уравнений Максвелла.
Date: 2015-07-17; view: 949; Нарушение авторских прав