Общие сведения. Показатели надёжности – это вероятность определённых событий, обусловленных свойствами привода

Показатели надёжности – это вероятность определённых событий, обусловленных свойствами привода.

Вероятность приобретает математический смысл и становится мерой Н., когда возможность проявления события оценивается числом устойчивым при не однократном повторении комплекса условий.

Теоретически вероятность события:

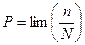
где n – число событий, N – число испытаний.

Её сложно определить, т.к. необходимо 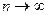и условия = const.

Более приемлемым остаётся определение вероятности, как некоторой величины, вблизи которой группируются частоты 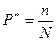при большом числе испытаний («статистическая» вероятность).

3.1. Показатели надёжности невосстанавливаемых приводов.

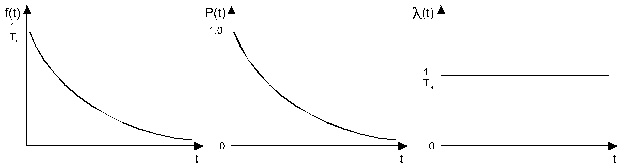
а) Интенсивность отказов.

Свойства элементов привода и его режим работы в допустимых приделах изменения внешних воздействий и условий эксплуатации изменяются случайно. Это приводит к возможности отказов в случайные моменты времени => время + раб. Элемента или привода до отказа – случ. Величина.

«Поток отказов» - последовательность отказов, наступающих один за другим.

«Поток событий» - последовательность событий, наступающих одно за другим.

Поток событий называется «одинарным», если вероятность показания на произв. интервал времени (t; t + Dt) 2-ух и более событий =0.

Поток событий называется потоком без последствия, если вероятность попадания R событий на интервал времени (t; t + Dt) не зависит от числа и моментов появления событий на других интервалах.

Ординарный без последствия поток называется пуассоновским. Число событий происходящих на любом интервале (t; t + Dt) распределяется по закону редких событий (Пуассона) и при этом, вероятность того, что случайная величина Х (число событий) в данный интервал, принимает значения 0,1,2,3…m равна m, выражается формулой:

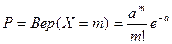
где, а – мат. Ожидание числа событий (параметр закона Пуассона)

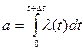
где l(t) – интенсивность отказов.

Интенсивность отказов – условная плотность вероятности возникновения отказа невосстановимого элемента, определяется для рассмотрения момента времени при условии, что до этого момента времени отказа не было.

Статистически:

,

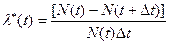где N(t) и N(t+Dt) – число элементов, работоспособных до момента времени t и

t + Dt; Dt – малый промежуток времени.

Вероятностная форма её выражения:

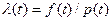
где f(t) – плотность вероятностей возникновения отказа; p(t) – вероятность безотказной работы за время t.

Если вероятность отказа на (t; t + Dt) зависит от числа отказов на интервале Dt и не зависит от положения начального интервала t, то такой поток называется стационарным. Интенсивность отказов практически для всех технических систем зависит от времени. Изменение l(t) во времени имеет три характерных участка.

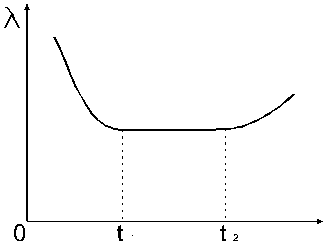
0-t1- период приработки (контрю технологические и производственные дефекты). Отказы описываются моделью «слабого звена». Для устранения отказов после сборки производится технологическая операция «приработка» (в стендовых или реальных условиях). Наилучшим режимом нагружения в этот период является (с позиции надежности) постепенное увеличение нагрузки.

Показателем колличества приработки может быть КПД, шум, температура, min мощность на холостом ходу.

На t1-t2 (период нормальной эксплуатации) 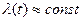, и определяется случайными, в основном внезапными отказами из-за влияния на приводы эксплуатационных факторов.

С момента t2 l(t) увеличивается из-за необратимых физико-химических процессов в элементах, связанных с длительной эксплуатацией. Механизм отказов объясняется моделями изнашивания, старения и усталости.

б) Вероятность безотказной работы.

Элемент работоспособен в t=0 и работает до первого отказа в случайный момент времени t. Надежность такого элемента полностью определяется безотказностью, а показатель безотказности – характеристика случайной величины t, которая есть время жизни (исправной работы) элемента.

Пологаем t- непрерывной величиной, т.к. невозможно предугадать моменты времени, когда отказ невозможен.

Обозначим функцию распределения величины t (вероятность отказа) через

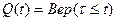
а плотность вероятности отказа через

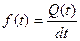
Вероятность безотказной работы – противоположная функция:

Вероятностью безотказной работы называют вероятностью того, что в пределах заданного промежутка времени отказ не произойдет. По стат. данным:

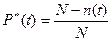
где N – число элементов, подвергнутых наблюдению, n(t) – число элементов, отказавших за время работы t/

При 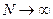, 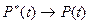P(0)=1 и при 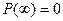, т.к.

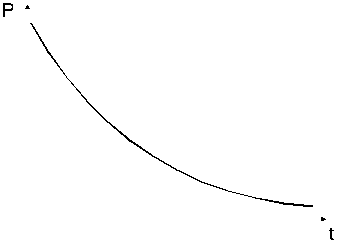
Зависимость вероятности безотказной работы от времени.

P(t) и l(t) имеют связь:

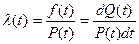или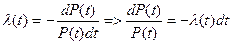

Проинтегрируем левую и правую части уравнения от 0 до t:

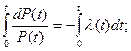
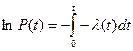, P(0)=1, ln P(0)=0,

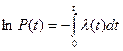или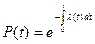

Важным для практики осв-ся случайной работы элемента при const инт. Отказов 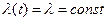при этом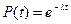

Это выражение экспоненциальным законом надежности.

Для P(t)>0 или l(t)<0,1 экспоненциальная зависимость заменяется 1-ым членом разл. функции:

P(t)=1-l(t)

Из-за отсутствия последствия отказов, подчиняющихся экспоненциальному закону приводит к тому, что вероятность безотказной работы на [t, t+Dt] не зависит от времени предшествующей работы, а зависит только от длинны инт. Dt.

в) Средняя наработка на отказ (среднее время безотказной работы)

Функции l(t) и P(t) являются исчерпывающими характеристиками надежности элемента. Однако имеет большое значение и Т0 – среднее время безотказной работы.

Т0 – есть математическое ожидание времени работы привода до первого отказа. Статистически определяется следующим образом. Пусть за время Т в процессе эксплуатации отказало n из N элементов. Время отказа каждого элемента: t1,t2,…tn. Тогда

.

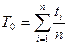Среднее время безотказной работы связано с ранее рассмотренными показателями т.к. Т0 есть м.о. t, то

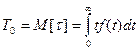
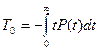
Возьмем интеграл по частям:

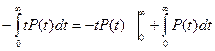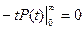т.к. , то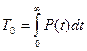

т.о. наработка на отказ численно равна площади под кривой P(t) ни интервале 0-¥.

Для эксп. закона надежности:

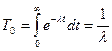
Эксп. закон является однопараметрическим и позволяет весьма просто вычислять вероятность безотказной работы, поэтому широко применяется в расчетах надежности. При этом не разграничивают постепенные и внезапные отказы. Условие l(t)=const – только для внезапных отказов. В машиностроении же преобладают постепенные отказы.

3.2. Показатели надёжности восстанавливаемых приводов.

а) Параметр потока отказов

Восстанавливаемые приводы характеризуются тем, что в процессе эксплуатации их работоспособность может быть восстановлена.

Функции восс-ых приводов характеризуются потоком отказов и восстановлении. Простейшей моделью описания этих потоков является такая модель, при которой элемент или привод в целом какое-то время (случайное) функционирует до 1-го отказа, затем следует его мгновенное восстановление в момент t1=t1, после чего элемент снова работает случайно в течении времени 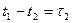до второго отказа и т.д.

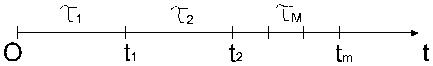
Модель функционирования восстанавливаемых приводов.

В начальный момент времени привод работоспособен. Моменты времени отказов t1,t2,…ti образуют случайный поток отказов.

Процесс восстановления описывается случайной величиной r(t), равной числу отказов, происходящих за время t. Величину r(t) можно характеризовать м.о. числа отказов на интервале ti M[r(t)]=W(t), которое называется ведущей функцией потока или функцией восстановления.

Часто используют не м.о. числа отказов, а его производную 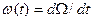, которую называют параметром потока отказов. Последний можно интерпретировать как среднее число 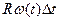восстановлении в интервале в интервале [t, t+Dt], если одновременно идет очень большое число независимых процессов.

Случайная величина r(t) имеет распр. с законом

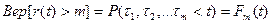
где 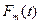- закон распределения случайной величины .

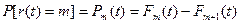Вероятность того, что за время t не произойет ни одного отказа (восстановления):

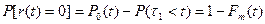
Вероятность того, что за время t не произойдет m отказов:

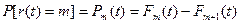
Имеем:

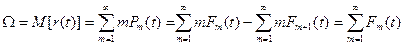
соответственно:

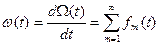
где 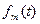- плотность вероятностей случайных величин t.

Функцию 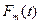определить сложно. При некоторых видах законов распределения можно получить простые формулы для параметра потока отказов.

Для эксп. закона распределения времени между отказами (восстановлениями) имеем:

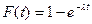и

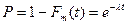
Процесс восстановления описывается пуассоновским потоком. Вероятность отказов:

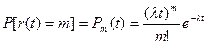
где l(t) – м.о. числа отказов.

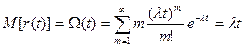
т.е. и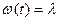

При нормальном распределении:

где Т0- среднее время безотказной работы.

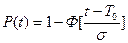
s - средне квадратное отношение наработки до отказа.

Закон распределения случайной величины t:

М.о. числа отказов:

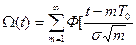
Параметр потока отказов:

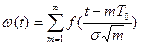
В статическом выражении:

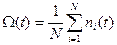
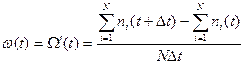
где N – число наблюдений, ni – число отказов.

При рассмотрении потока восст. необходимо учитывать специфич. ТОиР. (Поток восстановлении не есть следствие отказов, а определяется потенциальной возможностью отказа).

Поток отказов и восстановлении являются критериями для планирования ППР и длительности периода между ТО.

б) Вероятность безотказной работы.

(вер. – привод в любой момент времени находится в работоспособном состоянии).

Восстанавливаемый привод в произвольный период (t, t+Dt) будет в работоспособном состоянии в конце интервала Dt только при выполнении несовместных событий:

А – привод работоспособен в момент t и за интервал Dt не откажет.

В – привод к моменту времени t отказал, но за интервал Dt восстановлен.

Вероятности этих событий определяются зависимостями:

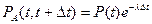
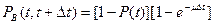
где m - параметр восстановлении (аналогичен параметру потока отказов); m=1/tвост

Разложим функции 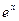в ряд и оставим только первые члены, получим:

,

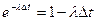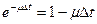
т.к. события А и В несовместны, то

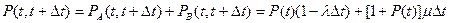
или

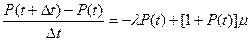
При 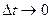имеем:

Решение этого д.у. при Р(0)=1 есть вероятность Рr(t) работоспособного состояния восст. привода в любой момент времени:

Для невосстановимого привода m=0 получаем (аналогично зависимости для пост. инт. отказов).

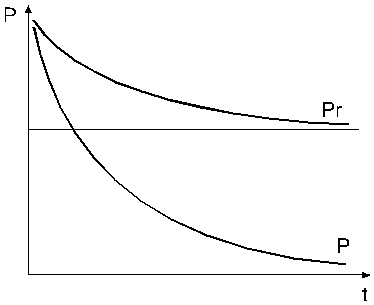
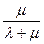
Вероятность безотказной работы для восстанавливаемых и не восстанавливаемых приводов.

Min вероятность безотказной работы восстанавливаемого привода определяется параметром восстановления, т.к. при , ,

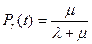Чем меньше время восстановления (больше m), тем 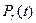больше.

Показатели безотказности восстанавливаемых приводов в основном применяются для разработки стратегии ТО. Для прогнозирования надежности в процессе эксплуатации применяются показатели долговечности.

в) Показатели долговечности

Долговечность – свойство привода сохранять работоспособность до наступления предельного состояния при установленной системе ТОиР.

Срок службы Тсл. – календарная продолжительность эксплуатации привода от её начала или возобновления после кап. Ремонта до наступления предельного состояния.

Ресурс Тр. – наработка привода от начала эксплуатации или её возобновления.

Тр. – является оценкой фактической наработки привода, а Тсл. – характеризует продолжительность функционирования привода с момента ввода в эксплуатацию независимо от характера использования.

Средний ресурс Тр.ср. (средний срок службы Тсл.ср.) – среднее значение ресурса (срока службы) совместимости приводов одного типоразмера и использования. Эти показатели определяются зависимостями:

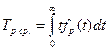
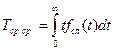
где 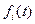- плотность распределения ресурса (срока службы).

Статистически эти показатели определяются аналогично наработке на отказ:

где 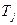- срок службы j – го привода.

Т.к. привод является подсистемой базовой системы, техннологические требования к ресурсным показателям для заданных условий и режимов эксплуатации определяют по значеним ресурсных показателй базовых машин. При этом ресурс привода:

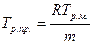
где R – коэф. использования привода в рабочем цикле машины;

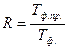
(Тор.пр. – время функционирования привода в техническом цикле, Тф. – время функционирования базовой машины); Тр.м. – средний ресурс машины; m – кратность замены или ремонта привода в доремонтный период базовой машины.

Гамма – процентный ресурс Трg - наработка в течении которой привод не достигает предельного состояния с заданной вероятностью g, выраженной в %. Тр.р. показывает, что g % приводов должны иметь наработку до предельного состояния не ниже значения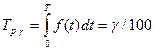

Приближенно:

4. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

4.1. Элементы теории вероятности при расчете надежности.

Отказы носят случайный характер, а сам отказ трактуют как случайное событие.

Вероятность события А – отношение числа возможных результатов испытания, благоприятствующих появлению события А и общему числу всех возможных результатов: .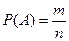

Случайное событие называют достоверным если в результате испытания онообязательно происходит. Случ. Событие которое заведомо не может произойти, называют невозможным.

Случайные события м.б. несовместными или совместными, независимыми или зависимыми.

Несовместными – называется 2 таких случайных события которые не могут произойти в одном и том же испытании.

Независимыми – называют такие события, когда появление одного из них не влияет на появление других.

При решении задач надежности используют такое понятие частоты события: w(А), которая представляет собой отношение результатов испытания, в которых событие А появилось к общему числу n результатов испытания:

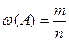
При неограниченном увеличении «n» w стремится к Р и является её приближенной оценкой. Частоту (w) называют статистической вероятностью.

Теоремы теории вероятности в рамках задач надежности.

1. Сложение вероятностей несовместных событий: вероятность S несовместных событий = S их вероятностей и равна вероятности того, что произойдет хотя бы одно из них.

Два несовместимых случайных события образующих полную группу т.е.

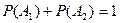
называются противоположными.

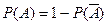, где - событие, противоположное А

2. Умножение вероятностей независимых событий: вероятность появления таких событий равна П их вероятностей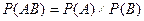

3. Умножение зависимых событий (вероятность появления одного из них зависит от появления или не появления другого). Для этого пользуются «условной вероятностью»: 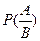- вероятность появления события А, при условии что событие В, имеющие Р(В)>0 уже произошло.

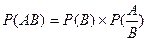
Случайные величины

С.в. называется величина, которая в результате испытаний начинает принимать 1 из возможных, заранее не известных значений.

С.в. называется дискретной, если она может принимать конечное или бесконечное счетное множество значений, т.е. если эти значения могут быть пронумерованы в количественном порядке.

С.в. называется непрерывной, если она может в результате испытания принять любое значение в 1 или нескольких заданных интервалах. Эти значения образуют несчетное бесконечное множество (континуум).

Для полной характеристики с.в. необходимо знать законы ее распределения.

Законом распределения – называется зависимость, устанавливающая связь между возможными значениями случайной величины и их вероятностями. Может быть задан таблично, графически или аналитически.

Закон распределения непрерывной случайной величины задают функцией распределения F(x) (интегральной функцией распределения), определяющей вероятность того, что случайная величина Х в результате испытаний примет значение, меньше х, т.е.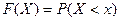

В надежности отказ представляется, как событие, состоящие в том, что

t<t => F(t) наработки t имеет физический смысл вероятности отказа объекта за время меньшее t: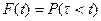

Тогда вероятность безотказной работы может быть найдена:

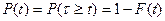
Функция Р(t) называется функцией надежности.

Наряду с F(t), применяют другую функцию, называемую “плотностью распределения” или “плотностью вероятности”. По её характеру можно судить о физической сущности и характере отказов.

Плотность распределения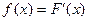

Свойства f(x):

1) ;

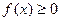2)

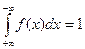
При расчетах надежности часто пользуются менее полными, но более простыми характеристиками с.в.: м.о. и Dx.

М.о. дискретной случайной величины называют SП всех её возможных значений на их вероятности:

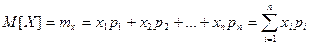
Для непрерывных величин:

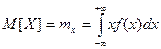
М.о. приблизительно равно арифметическому значению с.в.:

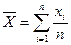
Центрированной с.в., соответствующей величине Х, называется отклонение с.в. Х от м.о.: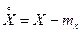

Дисперсией с.в. Х называют м.о. соответственной центрированной величины.

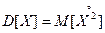
Dx характеризует степень рассеивания с.в. относительно м.о.

Формулы вычисления Dx:

- для дисперсных с.в.: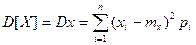

- для непрерывных с.в.: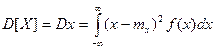

Для оценки рассеяния с.в. используется также среднеквадратичное отклонение:

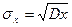
4.2. Законы распределения наработки до отказа.

1 из необходимых операций – определение на основании статических данных закона распределения различной величины.

1) Экспоненциальный закон

Характеризуется плотностью распределения наработки (времени) до отказа (плотностью вероятностей отказов) 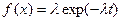, где l - интенсивность отказов (параметр закона распределения).

Функция распределения:

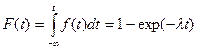
Вероятность отказа за время t:

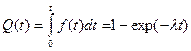
Вероятность безотказной работы (функция надежности):

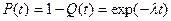
Средняя наработка (время работы) до возможного отказа равна м.о. наблюдаемых значений наработки до отказа (времени безотказной работы) объекта:

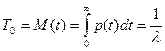
Дисперсия наработки до отказа:

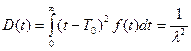
среднеквадратичное отклонение до отказа:

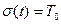
То – среднее время безотказной работы.

Интенсивность отказов:

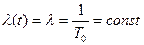
Экспоненциальный закон может использоваться и по отношению ко времени восстановления:

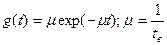
g(t) – плотность распределения времени восстановления,

m - интенсивность (параметр потока восстановления)

tв – среднее время восстановления

2) Закон Вейбусла, имеет 2 параметра и задается плотностью распределения вероятностей наработки до отказа:

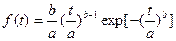
и функцией распределения:

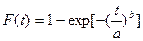
а – параметр масштаба (по оси х);

b – параметр формы (острота и симметрия)

а и b всегда >0

Функция надежности: ;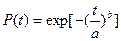

Вероятность отказа: ;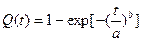

Интенсивность отказов: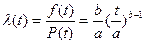

Широкое распр-ие, т.к. подбирая значения параметров можно добиться более полного соответствия.

При b=1, распределение B переходит в exp.

Хорошо описывает усталостные отказы: отказы объектов, состоящих из последовательно соединенных дублированных элементов и т.п.

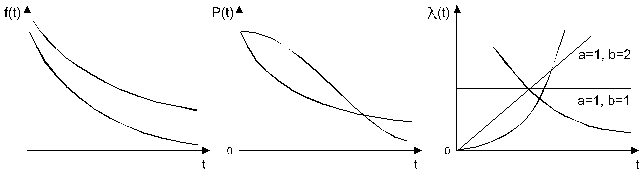
3) Нормальный закон

Хорошо описывает распределение вероятностей до отказа объектов, когда она зависит от большого числа однородных по влиянию случайных факторов, влияние каждого из которых незначительно. Характерны для постепенных отказов.

Плотность распределения:

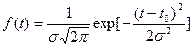
Функция распределения:

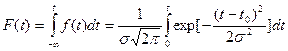
где t0 – м.о. наработки до отказа, s - среднеквадратичное отклонение наработки до отказа.

t0 – характеризует отклонение центра группирования по оси х; s - форму кривой f(t).

Характерным признаком нормального распределения – монотонное возрастание 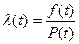с момента начала эксплуатации объекта.

Вероятность отказа (0,t):

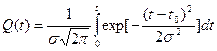
Вероятность безотказной работы:

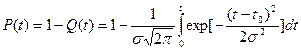
Ос-ть нормального распределения – 99,73% случайной величины укладывается на участке .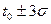

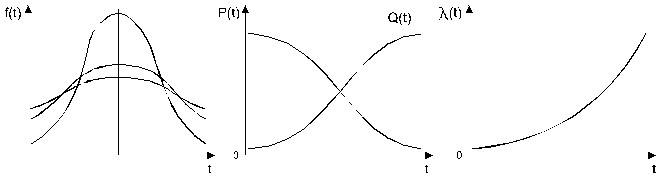
4) Закон гамма – распределения.

Распределение наработки до отказа резервированных объектов, элементы которых имеют экспоненциальное распределение наработки до отказа.

Плотность распределения:

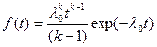
Если k – целое число, то функция раскрывается:

где k – параметр формы (число элементов или число отказов),

l0 – масштабный параметр (интенсивность отказов во время испытания).

Вероятность безотказной работы:

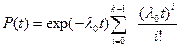
k-1 – число резервных элементов.

Средняя наработка до k-го отказа не резервируемого объекта при 1 испытании = м.о. набл. Значению наработки до отказа:

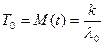
Дисперсия: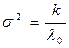

Интенсивность отказов: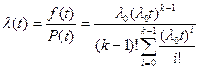

При k=1 закон гамма распределения превращается в экспоненциальный,

k>1 l(t) ­; k<1 l(t) ¯.

Гамма-распределение может хорошо описывать наработку до отказа (время до возможных отказов) сложных систем, если имеют место мгновенные отказы элементов в начальной стадии эксплуатации или в процессе приработки систем.

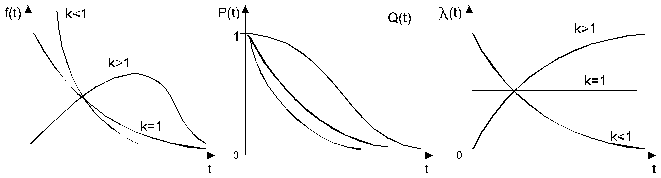
Наиболее универсальным является закон Вейбусла, т.к.:

1) Экспоненциальный и некоторые другие законы являются частными случаями закона Вейбусла при соответствующем коэффициенте формы;

2) Усеченное нормальное распределение описывается хорошо распределением закона Вейбусла при d>3,5.

3) Логарифм распределения аппроксимируется распределением закона Вейбусла так, что для получения стат. различия между ними необходимо больше 1000 испытаний.

3. Источники информации о надежности привода

Основная трудность определения показателей надежности заключается в том, что они характеризуют работу привода за длительный период времени, в то время как они должны быть заложены ещё на этапе проектирования.

На практике используются 3 основных источника о возможной потере работоспособности привода в процессе эксплуатации, аналитические расчеты и прогнозирование надежности на этапе проектирования, результаты испытаний на надежность, данные эксплуатации и ремонтов.

Наиболее ценную информацию о действительных показателях надежности и в частности сроках службы отдельных элементов привода, получают при Т.О.

Данные о сроках службы элементов привода в процессе эксплуатации и ремонта, позволяют судить о показателях надежности с учетом различных режимов работы и условий эксплуатации и могут быть использованы при проектировании новых приводов.

Всю информацию об испытаниях, эксплуатации и ремонте приводов группируют по количественным (год изготовления, № привода, дата ввода в эксплуатацию, дата появления неисправности, время восстановления, наработка на отказ.) и по атрибутивным (тип изделия, режим эксплуатации, характер и причины неисправности и т.п.) признакам. Вся информация в соответствие с ГОСТами.

Совокупность всех испытаний и результатов наблюдений, которые могут быть в данных условиях, называется генеральной совокупностью, а результаты, полученные при испытаниях, - выборкой из генеральной совокупности. Различают два вида генеральных совокупностей: бесконечную и конечную.

Конечной генеральной совокупностью является, например, партия N изготовленных приводов, из которой для анализа надежности под наблюдение поставлено n<N случайно выбранных приводов.

Если же предметом анализа, является, например, технологический процесс, то те же приводы следует считать, как выборку из бесконечной совокупности, которые могут быть изготовлены по данной технологии.

Выборка называется представительной (репрезентативной), если она достаточно широко представляет генеральную совокупность.

Для оценки искомых характеристик проводят статистическую обработку данных наблюдений. Пусть имеется случайная величина х с законом распределения F(x). В результате испытаний получена выборка 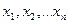, которую подвергают статистической обработке. В итоге получают статистики 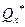параметра х. Статистиками может быть м.о., дисперсии и др. Т.к. выборка 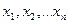имеет случайный характер, то и статистика случайна, может характеризоваться законом распределения F(Q) и числовыми характеристиками этого закона: м.о 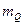, дисперсией 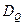и др. Обычно стараются получить не смещенные и эффективные оценки.

Для несмещенной оценки ее м.о. совпадает с истинным значением оцениваемым параметром:

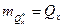
Эффективная оценка для данного объема выборки имеет min дисперсию.

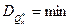
С увеличением объема выборки плотность вероятностей 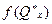оценки 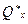приближается к истинному значению 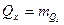, т.е. дисперсия оценки 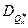с ростом объема выработки стремится к 0. Когда испытана вся генеральная совокупность, случайная величина превращается в неслучайную (детерминированную). В реальных условиях выборка всегда меньше 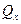генеральной совокупности, поэтому необходимо определить достоверные оценки. Эту задачу решают в 2 этапа. Сначала производят первичную обработку результатов испытаний, при этом определяют эмпирические функции распределения и статистики, а затем теоретические функции распределения с помощью различных критериев согласия.

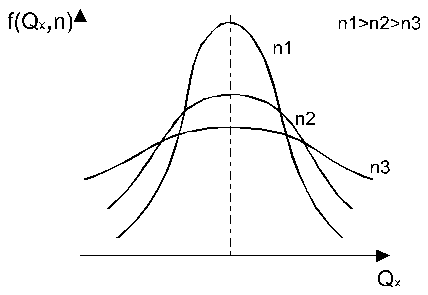
Зависимость дисперсной оценки от объема выборки.

4. Критерии согласия статистик Колмагорова

Для оценки совпадения (согласия) эмпирических и теоретических статистик применяют различные критерии согласия.

Критерий К. целесообразно применять при малых объемах выборки и известных априори характеристиках теоретического закона распределения. Для испытания критерия строят на одном графике теоретическую F(x) и эмпирическую F^*(x) кривые распределения и найти наибольшее абсолютное отклонение между этими функциями:

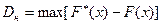
Согласие законов распределения определяют по вероятности:

(*)

где n – число отказов; - значение критерия k.

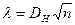
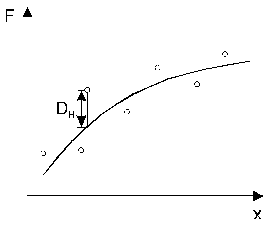
Если 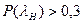, то согласие между теоретическим и эмпирическим законами распределения можно считать хорошим. Если 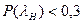, то это означает, что вероятность такого случайного отклонения эмпирической функции теоретически мала. Т.е. отклонение F^*(x) от F(x), по видимому, не случайно, т.е. формула F(x) недостаточно хорошо согласуется с F^*(x).

По уравнению (*) можно определить границу, в которой будет находиться неизвестная формула распределения F(x), при помощи известной из опыта F^*(x). Для этого запишем уравнение в виде неравенства:

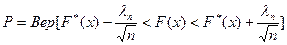
Определим верхние и нижние границы:

; (**)

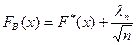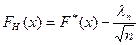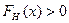, а 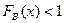- всегда; если по уравнениям (**) получаются значения меньше 0 и больше 1, то следует принять равными 0 и 1 соответственно.

5. Определение надежности привода на этапе проектирования.

5.1 Общие положения

Этап проектирования является определяющим в обеспечении надежности. Основные задачи расчета и исследования надежности на этом этапе можно разделить на три группы:

1) Обоснование требований по надежности к основным элементам привода (Нормирование надежности). (На ранней стадии проектирования, обоснование принципов проектирования).

2) Обеспечение надежности элементов и привода в целом. (Возможные способы обеспечение надежности, выбор проектных характеристик, запасов прочности, выбор оптимальных конструкций).

3) Контрольные расчеты надежности привода по проектным данным.

Этап производства с точки зрения надежности является связующим звеном между этапом проектирования и эксплуатации. В процессе производства требуется изготовить привод с уровнем надежности, заданным на этапе проектирования. Производство сопровождается действием объективных и субъективных факторов, которые в совокупности могут снижать надежность. Их можно разделить на две группы:

А) Факторы, действие которых приводит к грубым нарушениям технологического процесса, погрешностям изготовления, монтажа, появлению скрытых дефектов, приводит к потере работоспособности.

Б) Факторы, действие которых приводит к непредсказуемым частичным изменениям начальных свойств элементов и материалов, снижающих надежность.

Проведение сплошного контроля для обнаружения дефектов, обусловленных функциями группы А и особенно группы Б, требует больших затрат. Поэтому на практике используют выборочный контроль, которому подвергают только некоторую случайную выборку из партии (Идея – академик М.В. Остроградский, 1846 г.).

При организации контроля задают ошибки 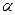(вероятность забракования данной партии при приемке – риск поставщика) и 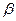(вероятность пропуска брака при приемке изготовленной продукции – риск потребителя),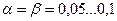

и вводят оперативную характеристику контроля, т.е. функцию 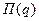, равную вероятности принятия партии, содержащей долю дефектных изделий 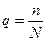, (n – число дефектов изделия в партии объемом N).

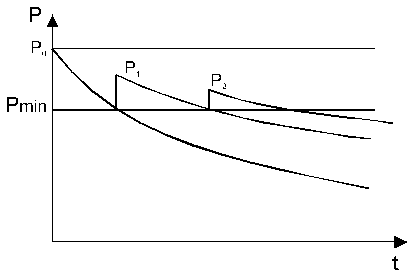
На этапе эксплуатации привода практически выявляется достигнутый уровень надежности. Из-за влияния на него возмущающих факторов его надежность изменяется. Когда надежность становится минимальной, привод ремонтируют. В результате ремонта и замены вышедших из строя элементов вероятность безотказной работы повышается до Р1, однако из-за выработки ресурса оставшихся элементов новый уровень будет ниже первоначального Р0, т.е Р2<Р1<Р0.

Для количественной оценки надежности на этапе проектирования и производства широкое распространение получили методы не превышения и структурных схем. В общем случае они применяются, совместно дополняя друг друга. В то же время, в зависимости от задачи анализа надежности и располагаемого объема информации, каждый метод имеет преобладающее значение.

Метод не превышения – используется в случае определения надежности по отношению к постепенным отказам и надежности по отношению к прочности конструкции.

Метод структурных схем – используется при анализе надежности по отношению к внезапным отказам.

5.2. Общее уравнение надежности привода

В общем случае привод включает в себя источники питания, усилители и распределители мощности, устройства управления, исполнительный орган и вспомогательные устройства.

Т.о. привод является сложной системой взаимосвязанных узлов, агрегатов и элементов, т.е. упорядоченной совокупностью взаимосвязанных и взаимодействующих элементов, образующих единое целое. Привод как система характеризуется структурой и функциями. Под структурой привода понимают совокупность элементов и взаимные связи между ними, под функцией – совокупность всех возможных действий.

Для анализа надежности, сложных системы разбивают на элементы.

Элементом – называют совокупность различных технических средств, которые при данном исследовании рассматриваются как одно неделимое целое. Элементы характеризуются тем, что они имеют самостоятельные входные и выходные сигналы управления.

Сначала рассматривают характеристики элементов, а затем оценивают надежность системы в целом.

Выходные параметры элементов по разному влияют на формирование выходного параметра всей системы, определяя ее надежность. В зависимости от этого можно выделить три основных группы этих параметров:

1) Параметры, которые влияют на работоспособность только самого элемента;

2) Параметры, участвующие в формирование выходного параметра всей системы;

3) Параметры, влияющие на работоспособность других элементов.

В зависимости от преобладающих свойств элементов формируют основные методы анализа надежности. Система, состоящая из элементов с параметрами 1-ой группы, является системой с независимыми элементами. Для ее надежности необходима надежная работа каждого элемента в отдельности.

Для приводов характерно наличие параметров 2-ой группы. В этом случае элементы нельзя считать независимыми, необходимо рассматривать систему в целом и учитывать, как участие каждого элемента в формировании надежности всей системы, так и их взаимное влияние на работоспособность.

При расчете надежности сложных систем все элементы целесообразно разбить на три группы:

1) Элементы, работоспособность которых практически не влияет на работоспособность системы (корпусные детали).

2) Элементы за рассматриваемы промежуток времени практически не изменяются (корпусные детали, малонагруженные элементы с большим запасом прочности).

3) Элементы отказы, которых приводят к отказу привода.

Анализируются только элементы третьей группы.

В сложных системах безотказная работа системы является необходимым но не достаточным условием надежности всей системы. Это объясняется тем, что в сложных системах большую роль играют взаимосвязи элементов. Работоспособные элементы могут воздействовать на другие элементы и вывести их из строя (износ). Кроме того, малые изменения параметра в пределах допустимого могут дать такие сочетания, которые неблагополучно отразятся на работоспособности всего привода. Т.о., при анализе надежности привода как сложной системы необходимо учитывать взаимосвязь элементов.

Модель надежности привода должна устанавливать функциональную связь между показателями надежности привода как системы с показателем надежности его элементов.

В общем виде вероятность безотказной работы привода может быть описана уравнением вида: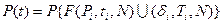

где F(…) – функционалное представление структуры привода и взаимосвязь его элементов в любой момент времени.

- вероятность безотказной работы i-го элемента.

N – число элементов привода.

U(…) – оператор определяющий степень влияния на показатель надежности возмущающих факторов.

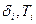- объем и регламент т.о. i-го элемента в процессе эксплуатации.

Так как привод состоит из функционально зависимых и взаимосвязанных элементов, в процессе работы между ними имеет место статистическая связь.

Пусть число элементов привода равно N и для каждого элемента априори известны показатели надежности, например вероятность безотказной работы . Любой из элементов может находится в 2-х состояниях: А – исправном (безотказном) и - неисправном, то есть в состоянии отказа. В этом случае вероятность того, что совместно произойдет N событий А (все элементы привода находятся в исправном состоянии), определяется зависимостью:

.

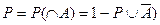Между событиями 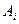и (вероятностями безотказной работы элементов i и j) имеет место корреляционная связь, которая определяет коэфициент корреляции:

,

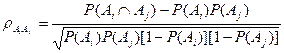где 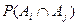- вероятность одновременного появления событий 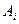и ;

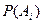- вероятность появления события .

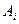Из ряда уравнений получим выражение для вероятности безотказной работы привода как системы состоящей из N зависимых элементов:

, (*)

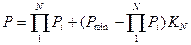где 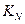- коэффициент учитывающий статическую связь между отказами элементов:

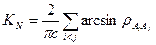
где i<j – коэффициент корреляции , , …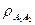

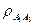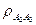В зависимости от степени статической связи между отказами элементов возможны следующие частные случаи:

1) 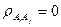(статическая связь отсутствует); ,

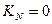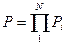
Это означает, что надежность системы состоит из N независимых элементов, определяется произведением вероятностей безотказной работы отдельных элементов.

2) 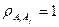(все элементы статически зависимы) ,

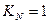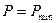
Если элементы привода зависимы, то вероятность безотказной работы системы определяется вероятностью работы наименее надежного элемента (модель «слабого» звена).

Соотношение (*) удобно для оценки надежности систем при проектировании, так как оно не связано с допущением о виде закона распределения рассматриваемых случайных величин или их векторов.

5.3. Метод не превышения или «несущая способность – нагрузка».

Одной из основных задач при проектировании привода является построение такой конструктивной схемы, при которой основные характеристики элементов и привода находятся в некоторых приделах, гарантирующих выполнение приводом его функций. Условия успешного функционирования привода часто формируются в виде соотношений, отражающих требования не превышения некоторой функцией ее допустимых значений.

Надежность привода определяется соотношением допустимых 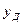и возможных 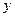значений выходных параметров.

Работоспособность характеризуется постоянной областью предельных состояний, выход за пределы которых классифицируется как отказ, то есть когда 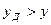. В общем случае границы работоспособности могут занимать случайное положение. При анализе надежности допустимые значения выходного параметра 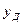, характеризуется предыдущим состоянием, задают. (установить нормативы 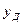трудно:

1) Допустимые значения задают для базовых машин, а не для привода;

2) Между выходными параметрами и степенью повреждений может существовать функциональная связь, отражающая структуру привода. Линейный закон измерения степени повреждений может привести к нелинейным временным изменениям выходного параметра, так как повреждение связано с физическими параметрами, а изменение выходного параметра – отражает макропроцесс, происходящий во всей системе).

В связи с этим, хотя предельное значение выходного параметра величина не случайная, при анализе надежности ее рассматривают как случайную с соответствующими статистическими характеристиками.

Под предельными характеристиками привода будем понимать такое его состояние, при котором действительная нагрузка равна несущей способности. Если обозначить нагрузку через R, а несущую способность через S, то условие не превышения (безотказности соответственно) запишем в виде R<S.

Несущая способность и нагрузка из-за влияния совокупности возмущающих факторов различной природы являющихся случайными величинами или функциями, имеющими нормальное распределение с плотностью вероятностей:

;

,

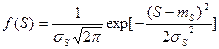где 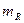и 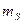- математическое ожидание нагрузки и несущей способност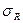и,

и 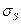- средне квадратичные отклонения.

В качестве нагрузки и несущей способности следует выбирать одни и те же физические параметры: деформации, напряжения…

Рассмотрим одно пред. сост. В качестве параметра состояния примем разность между несущей способностью и нагрузкой: Z=S-K

Кривые распределения несущей способности и нагрузки могут пересекаться то есть появляться области где нагрузки больше чем несущая способность, то есть нарушаются условия работы (отказ)

Значение Z задается композицией норя. распр., при которой снова получается нормальный закон распределения с м.о.:

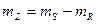
и дисперсией:

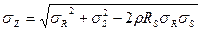
Плотность распределения величины Z:

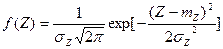
Вероятность того, что нагрузка не превысит несущую способность определяется уравнением:

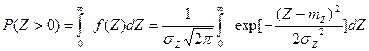
Переходя к нормированной функции Лапласа, получаем расчетную зависимость:

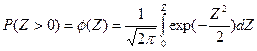
где -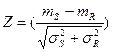

- если между несущей способностью и нагрузкой отсутствует статическая связь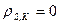

5.4. Статистический коэффициент запаса работоспособности (h)

Статистическим коэффициентом запаса работоспособности называется отношение м.о. несущей способности к м.о. нагрузки.

Коэффициент запаса выбирают для обеспечения работоспособности в случае появления неучтенных при проектировании факторов. В идеальном случае

h=1 (если параметры, привода строго детерминированы). Т.к. нагружающая и несущая способности – случайные функции, то h должен быть больше 1 и увеличивается с ростом Dx.

h вычисляют для всех определяющих параметров привода.

Вероятность выполнения условия не превышена:

или

где 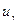- квантиль нормального распределения, 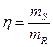- статический коэффициент запаса работоспособности, 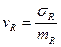- коэффициент вариации нагрузок,

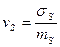- коэффициент вариации несущей способности.

Необходимый (обеспечивающий заданную вероятность работоспособности) коэффициент запаса:

,

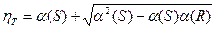где ;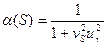

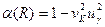
Если несущая способность детерминирована (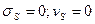), то коэффициент запаса прочности по нагрузке определяется только вариацией нагрузки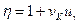

Когда детерминирована нагрузка ():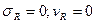

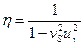
На h вариации нагрузки влияют меньше, чем несущие способности.

5.6. Метод структурных схем

При расчете надежности привода целесообразно представлять его как систему элементов, для которых можно определить показатели надежности.

Деление системы на элементы и влияние отказов элементов на надежность системы отражается структурными схемами надежности (ССН).

Метод СС применяют для расчета надежности, как вероятности внезапных отказов при условии, что все элементы системы являются одно-отказными (т.е. в элементах невозможны разные отказы одновременно) и отказы элементов независимы.

Основой структурных схем является изображение последовательно и параллельно изображенных элементов, выражающие события безотказности их действия. Последовательным считается соединение элементов, при котором отказ хотя бы одного из них приводит к отказу всей системы. Параллельным называется соединение элементов в системе, при котором отказ системы наступает только тогда когда откажут все элементы. В некоторых случаях система состоит из неполных подсистем с основным и резервированным соединением элементов. Такие системы называют системами с комбинированным (смешанным) соединением элементов.

Тип соединения элементов с структурной схеме зависит от влияния отдельных элементов на работоспособность всей системы и не всегда совпадает с монотонным соединением.

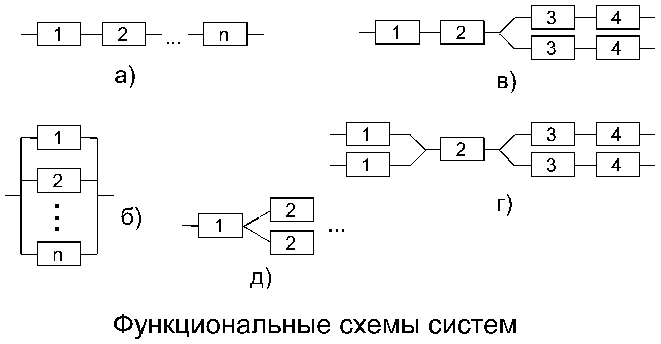
а) – последовательное соединение; б) параллельное соединение; в), г) – комбинированное соединение; д) – упрощенная система.

Система последовательного соединения элементов безотказна только в том случае, когда безотказны все элементы от 1-го до n. Вероятность безотказной работы последовательно соединенных элементов равна П вероятности появления всех событий: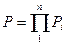

Система параллельно соединенных элементов безотказна, если безотказны оба элемента или хотя бы один из них: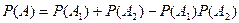

Если 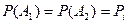, то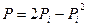

Для трех элементов включенных в схему параллельно: .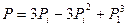

Если структурная схема состоит из k параллельных цепей, в каждой из которых n элементов, то вероятность безотказной работы системы:

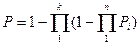
Сложные системы составляются по принципу прохождения сигнала, который состоит в том, что сигналы в сложных системах проходят только по исправленным элементам (отказавший элемент сигнал не пропускает). Так, при последовательном соединении элементов сигнал со входа на выход не проходит, если откажет хотя бы один элемент. При параллельном соединении для прохождения сигнала достаточно иметь хотя бы одну исправную ветвь.

В период эксплуатации интенсивность отказов не зависит от времени и справедлив экспоненциальный закон надежности.

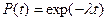
В этом случае, для последовательно соединенных n элементов:

,

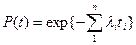где 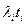- интенсивность отказов и время исправной работы i-го элемента.

Надежность системы с последовательным соединением элементов ниже надежности наименьшей надежности элемента. Чем сложнее система, тем ниже ее надежность при прочих равных условиях (оккам).

При параллельном соединении элементов вероятность безотказной работы:

(*)

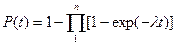Надежность параллельных соединений элементов при одинаковой их безотказности выше, чем надежность последовательного соединения.

Для высоконадежных элементов, когда справедливо неравенство 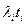<1 и имеем:

Простота расчета над сложными системами при экспоненциальном законе надежности часто приводит к тому, что этим правилом пользуются и в тех случаях, когда причина выхода из строя – постепенный отказ, что в общем случае – неверно.

Обычно при расчете надежности сложных систем считают, что вероятность безотказной работы каждого элемента известна или задана. При этом учитывают, что она формируется под влиянием различных процессов и является функцией времени.

Для каждого элемента характерна своя кривая наработки до отказа 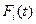. При изменении периода 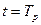(ресурс), в течении которого рассматривается работа системы, изменяется и для каждого элемента. Так, при изменении 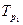до 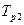вероятность отказа первого элемента возрастает в несколько раз, второй элемент становится критически не работоспособен, а третий элемент не лимитирует P(t), поскольку его область отказов находится в зоне .

Для оценки надежности такой системы не подходит экспоненциальный закон. Использовать формулу (*) необходимо с учетом зависимости от времени согласно той или иной модели отказов.

Для расчета надежности сколь угодно сложных систем достаточно знать состав элементов, их число, монтажные соединения и статические характеристики показателей надежности каждого элемента. Данные о составе элементов определяются по монтажной схеме, а показатели надежности приводов – на основании данных эксплуатации приводов, подобных проектируемым.

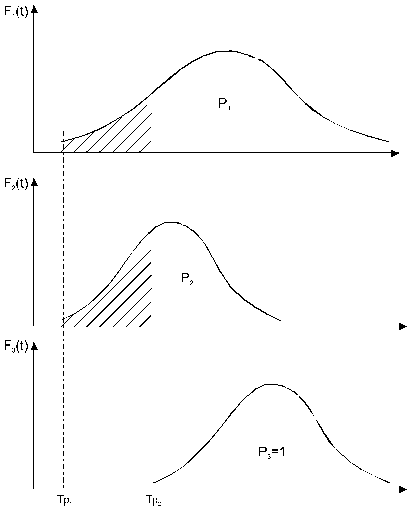
Схема формирования вероятности отказа

Расчет показателей надежности по структурным схемам целесообразно проводить по блокам и узлам привода. Это позволяет сравнить узлы по надежности