Графическое оценивание параметров распределений

Графическое оценивание параметра экспоненциального распределения.

Значения эмпирической функции распределения для экспоненциального распределения рассчитываются по зависимости:

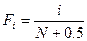, (3.4)

Получим:

; ; ; ;

; ; ; ;

; ; ; ;

; ; ; .

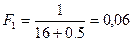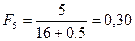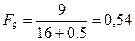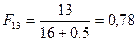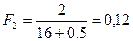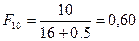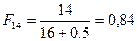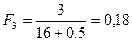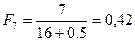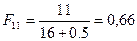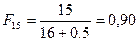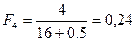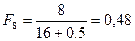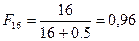Наносим на вероятностную сетку (см. прил.1) точки с координатами:

[7;6], [8;12], [8;18], [8;24], [9;30], [14;36], [15;42], [18;48], [22;54], [23;60], [36;66], [41;72], [48;78], [57;84], [70;90], [75;96] и проводим через них прямую. Абсцисса точки с ординатой 63.8 соответствует величине 28.7, тогда параметр:

.

Графическое оценивание параметров распределения Вейбулла.

Оценивание параметров распределения Вейбулла можно найти по вероятностной сетке (см. прил.2), используя зависимость:

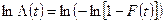; (3.5)

,

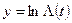где 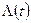- накопленная интенсивность отказов.

Вычисление накопленной частоты отказов производят в следующей последовательности:

- наработки до отказа и до цензурирования выстраиваются в вариационный ряд;

- для каждого значения 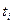вычисляются соответствующие значения оценки накопленной интенсивности отказов:

; ,

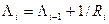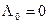где 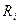- инверсионный номер изделия, то есть ранг, отсчитанный с конца вариационного

ряда.

Если точки с координатами [lnLi;lnti] на вероятностной сетке удовлетворительно апроксимируются прямой, то переходят к оценке точечных значений параметров a и b.

Пересечение полученной прямой с линией, проведенной параллельно оси абсцисс из точки с ординатой y= 0, дает точку, абсцисса которой характеризует точечную оценку параметра а.

Точка пересечения прямой, проведенной из специальной точки А параллельно построенной прямой, со шкалой b дает искомую оценку параметра b.

Оценка параметра а равна абсциссе точки пересечения построенной прямой и линией, проведенной из точки с ординатой F(x)=0,623 или у=0.

Вычисления накопленной частоты сведем в таблицу 6.

Наносим на вероятностную сетку точки с координатами [x=t;y=lnΛ_i] и проводим через них прямую.

Пересечение прямой с линией, проведенной параллельно оси абсцисс из точки с ординатой y=0, дает оценку параметра а:

а=33.

Из точки А проводим луч параллельно построенной прямой до пересечения со шкалой b. Точка пересечения дает оценку параметра b=1.35.

Таблица 6

I
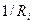
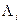
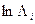
			0,063	0,063	-2,76
			0,066	0,129	-2,05
			0,071	0,20	-1,61
			0,077	0,27	-1,28
			0,083	0,36	-1,02
			0,091	0,45	-0,80
			0,10	0,55	-0,60
			0,11	0,66	-0,40
			0,13	0,79	-0,20
			0,14	0,93	-0,07
			0,17	1,10	0,09
			0,20	1,30	0,26
			0,25	1,55	0,44
			0,33	1,88	0,63
			0,50	2,38	0,87
			1,00	3,38	1,22

Графическое оценивание параметров нормального распределения.

Значения эмпирической функции распределения для нормального распределения рассчитываются по зависимости:

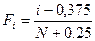. (3.6)

Получим:

; ; ; ;

; ; ; ;

; ; ; ;

; ; ; .

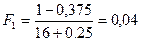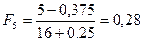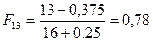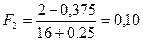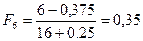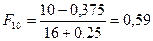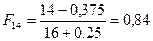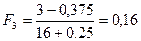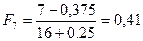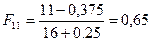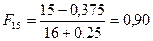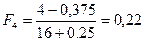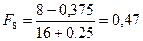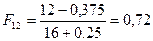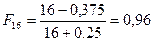На вероятностную сетку (см. прил.3) наносим точки с координатами:

[17;4], [25;10], [29;16], [43;22], [57;28], [96;35], [115;41], [142;47], [155;53], [170;59], [174;65], [180;72], [190;78], [230;84], [235;90], [260;96].

Date: 2015-07-17; view: 331; Нарушение авторских прав