Проверка статистической гипотезы о соответствии экспоненциальному распределению

Для проверки статистической гипотезы наиболее мощным является критерий Бартлетта:

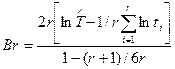, (2.1)

где 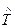- оценка средней наработки до отказа;

r – число наработок до отказа;

t_i – значение i-той наработки.

Все вычисления сведем в таблицу:

Таблица 1

N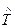
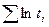
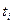
																	28,7	---
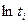
		2,1	2,1	2,1	2,2	2,6	2,7	2,9	3,1	3,2	3,6	3,7	3,9		4,2	4,3	---	48,6

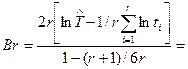
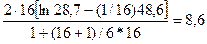
Выполняется условие:

;

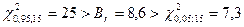где 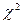для заданного уровня значимости 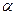, числа отказов r находится из табл. 5 прил., следовательно гипотеза о принадлежности выборки к экспоненциальному распределению не отвергается.

Проверку можно осуществить и с помошью критерия Пирсона:

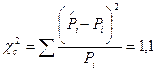, (2.2)

где 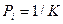- теоретическая частота, 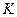- число интервалов.

Все вычисления сведем в таблицу:

Таблица 2

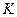
	1-12	12-24	24-36	36-48	48-60	60-75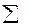
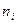
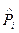
	0.31	0,31	0,0625	0,125	0,0625	0,125
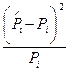
	0.14	0,14	0,06	0,0077	0,06	0,0077	0,425

Число интервалов - .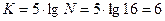

Протяженность интервалов - .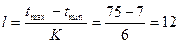

Теоретическая частота -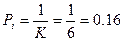

Для 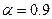и к-2=6-2=4 по табл.5 прил. находим -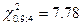

Так как соблюдается неравенство:

,

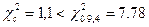то гипотеза о принадлежности выборки к генеральной совокупности, описываемой экспоненциальным распределением, не отвергается.

Date: 2015-07-17; view: 408; Нарушение авторских прав