Модель Миллса

Пусть в процессе тестирования обнаружено n исходных ошибок и v из S рассеянных ошибок. Тогда оценка N - первоначальное число ошибок в программе - составит

. (16)

Вторая часть модели связана с проверкой гипотезы выражения и тестирования N.

Рассмотрим случай, когда программа содержит К собственных ошибок и S рассеянных ошибок. Будем тестировать программу до тех пор, пока не обнаружим все рассеянные ошибки. В то же время количество обнаруженных исходных ошибок накапливается и запоминается. Далее вычисляется оценка надежности модели:

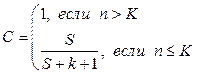(17)

как вероятность того, что в программе содержится K ошибок.

Величина С является мерой доверия к модели и показывает вероятность того, насколько правильно найдено значение N. Эти два связанных между собой по смыслу соотношения образуют полезную модель ошибок: первое предсказывает возможное число первоначально имевшихся в программе ошибок, а второе используется для установления доверительного уровня прогноза.

Формула для расчета С в случае, когда обнаружены не все искусственно рассеянные ошибки, модифицирована таким образом, что оценка может быть выполнена после обнаружения v (v£S) рассеянных ошибок:

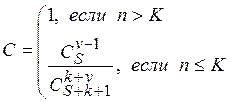(18)

где числитель и знаменатель формулы при n £ К являются биноминальными коэффициентами.

Пример 3.

Предположим, что в программе имеется 3 собственных ошибки. Внесём ещё 6 ошибок случайным образом. В процессе тестирования было найдено:

1) 6 ошибок из рассеянных и 2 собственных;

2) 5 ошибок из рассеянных и 2 собственных;

3) 5 ошибок из рассеянных и 4 собственных.

Найти надёжность по модели Миллса - С.

K=3, S=6.

1) n=2, v=6, C=(6!/(6-1)!)/((6+3+1)!/(3+6)!)=0,6.

2) n=2, v=5, C=(6!/(5-1)!)/((6+3+1)!/(3+5)!)=0,333333, 2!=2, 4!=24, 6!=720, 8!=40320, 10!=3628800.

3) n=4, v=5, C=1 (по формуле (18)).

Date: 2015-07-17; view: 8783; Нарушение авторских прав