Схемы с неравномерным движением регистров

· управление с помощью управляющего регистра

· самоуправление с помощью обратной связи

Генераторы «стоп-вперед»

Схема работы выглядит следующим образом. Первый регистр движется равномерно (1 знак за 1 шаг). Если знак равен 0, то регистр 2 не движется и выдает тот знак, который у него был до этого. Если же знак равен 1, то регистр 2 сдвигается (отрабатывает) 1 такт и на выходе выдается значение функции обратной связи

«0» - оставляем, что было.

«1» - прокручиваем новое.

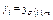
- суммарное число продвижений.

Из линейной последовательности строим гамму достаточно сложной зависимости. Сама же функция f довольно простая,

Слабости: По выходной последовательности можно судить о входе.

Пусть Т₁ – период первого регистра, Т₂ – второго регистра, Т – период всего генератора.

- сумма всех продвижений за период. То через НОК (S,T₂) шагов второй регистр вернется в исходное состояние. И за каждый круг первого регистра происходит продвижение на S шагов =>

Можно построить схему так, что НОД (S,T₂)= 1 (взаимнопростые числа), тогда Т = Т₁ Т ₂

- линейная сложность. Равенство будет в том случае, если (m,n)=1 и Т₁=2ⁿ-1

Эта схема довольно сложная, однако генератор обладает слабым криптографическим свойством:

если 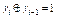, то произошел сдвиг второго регистра , таким образом можно восстановить первый регистр, набирая информацию. Чтобы исключить эти слабости, используется генератор «1-2 шага». Для этого генератора функция управления . Если , то R₂ сдвигается на 1 шаг. Если , то R₂ сдвигается на 2 шага.

Обобщением описанных моделей является генератор BRM = Binary Rate Multiplier.

Управляющая функция имеет вид: - функция от t первых координат первого регистра. . Число единиц на периоде первого регистра: .

За число импульсов на входе R₂: - оба регистра вернуться в исходное состояние.

Т.о. - период всего генератора, где - сколько кругов совершит второй регистр, пока они оба придут в начальное состояние. Можно подобрать регистры так, что , тогда - период максимален.

Вывод 1: период общей последовательности генераторов «стоп-вперед» и «1-2 шага» равен произведению периодов, входящих в них регистров.

Для линейной сложности: , где m – длина R₂. Это оценка сверху. Она достигается, если НОД(m,n)=1, а R₁ – полноцикловый.

(Преобразование А называется полноцикловым, если его граф образует один полный цикл).

Вывод 2: генераторы «1-2 шага» и «стоп-вперед» имеют следующие достоинства:

1. Большой период

2. Высокая линейная сложность

3. хорошее статистическое свойство (все - граммы, 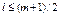, встречаются равномерно)

Главный недостаток: если знать как работал управляющий регистр R1, легко восстановить всю выходную последовательность.

Генераторы с «перемежающимся шагом»

Есть 1 управляющий регистр и 2 «генерирующих» регистра.

Длина регистра R₁ = n, R₂ = m, R₃ = r.

Заполнение на i-ом такте: - 1 регистр, 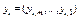- 2-ой регистр, - 3-ой регистр.

R₁ выдает управляющие символы:

· если «1», тогда продвигается R₂, а R₃ стоит на месте.

· если «0», тогда продвигается R₃, а R₂ стоит на месте.

Т.о. , где - продвижка регистра R₂.

Если периоды R₂, R₃ взаимно просты (), а характеристический многочлены и неприводимы и неравны, и период регистра R₁ , то период выходной последовательности (g) максимален и равен . Линейная сложность выходной последовательности ограничена величинами: - очень неплохие границы.

Статистическое свойство: если R₂ и R₃ – полноцикловые регистры (имеют максимальный период), то частота появления всех - грамм, где , приблизительно равна - почти что равномерное распределение. При этом можно указать порядок погрешности: .

Недостатки: если знать движения регистров R₂ и R₃, то выходная последовательность получается линейной функцией от знаков R₂ и R₃. Т.о. стойкость системы определяется возможностью «пробивания» R₁. Сложность определения ключа: .

Каскадный генератор

R₁ работает равномерно, управляя движением R₂; R₂ управляет движением R₃ и т.д. … последний регистр R_N выдает гамму, где N – длина каскада.

Можно подобрать так, что Т = Т₁^N (L- длина регистров)

Берут N≥10, L≈100 чтобы зависимость γ от γ(1) была довольно слабой, последний регистр почти всегда «отдыхает».

Сжимающий генератор

Оба регистра движутся равномерно. Выходной является знак R₂, если выход R₁ = 1 (на i-ом шаге). Если же R₁ = 0, то он запрещает вывод знака R₂ в линию (этот знак просто отбрасывается).

N(i) – номер такта, который соответствует i-ой единице в выходной последовательности R₁.

Недостаток: знаки гаммы выдаются на выход не равномерно (Может быть большая задержка если долгое время на выходе будут нули). Это исправляется путем проведения буферизации. Емкость буфера определяется свойствами выходной последовательности R₁.

Date: 2016-08-30; view: 504; Нарушение авторских прав