Вопрос 53.2 Однонаправленные функции и однонаправленные функции с секретом, их применение

Понятия однонаправленной функции и однонаправленной функции с секретом являются центральными понятиями всей криптографии с открытым ключом. Рассмотрим два произвольных множества X и Y. Функция f: X ® Y называется однонаправленной, если f(x) может быть легко вычислена для каждого x из X, тогда как почти для всех y из Y вычисление такого x из X, что f(x) = y (при условии, что хотя бы один такой x существует), является сложным. Это понятие не нужно путать с функциями, которые являются математически необратимыми из-за того, что они не взаимнооднозначны (т.е. из-за того, что существует несколько различных x, таких что f(x) = y, или их нет вовсе). Наше нынешнее состояние знаний не позволяет нам доказать, что однонаправленные функции вообще существуют, так как их существование разрешило бы (P = NP)- проблему. Более того, теория NP-полноты не кажется вполне компетентной для того, чтобы обеспечить даже простое обоснование их существования.

Простой пример кандидата на однонаправленную функцию целочисленное умножение. Известно, что умножать даже очень большие числа относительно нетрудно, в то время как даже самый мощный компьютер не в состоянии разложить на множители с наилучшим имеющимся в его распоряжении алгоритмом двухсотзначное десятичное число, являющееся произведением двух примерно одинакового размера простых чисел.

Конечно, необходимо понимать, что "не в состоянии" означает "не в состоянии за приемлемое время (такое, как время человеческой жизни или возраст вселенной)".

Другим важным примером кандидата на однонаправленную функцию является модульное возведение в степень или модульное экспонирование (с фиксированными основанием и модулем). Пусть n и a - целые числа, такие что 1 < a < n, и пусть Zn = { 0,1,2,...,n-1 }. Тогда модульное возведение в степень (относительно основания a и модуля n) это такая функция f[a,n]: Zn -> Zn, определяемая как f[a,n](m) = a^m mod(n), где i mod(j) обозначает положительный остаток при делении i на j. Сразу не очевидно, что такую функцию можно вычислить эффективно, когда длина каждого из трех параметров a, n и m составляет несколько сотен знаков. То, что это возможно и в самом деле так, лучше всего увидеть на примере: . Он показывает, как можно вычислить 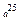c помощью лишь четырех возведений в квадрат и еще двух умножений. При вычислении произведение по модулю n желательно делать после каждого возведения в квадрат и каждрого умножения, чтобы избежать получения очень больших целых чисел. Если экспонента m является числом длиной в L битов, то следующему рекурсивному алгоритму, для того чтобы вычислить , требуется от L до 2L модульных умножений (считая умножением и возведение в квадрат).

По аналогии с действительным анализом обратная операция известна как задача дискретного логарифмирования: даны целые числа a, n и x, требуется найти такое целое m (если оно существует), что = x. Например, . Следовательно, 4 это дискретный логарифм 16 с основанием 5 по модулю 21. При желании можно проверить, что, например, число 3 вообще не имеет логарифма с основанием 5 по модулю 21. Несмотря на то, что вычисление больших модульных экспонент может быть осуществлено эффективно, в настоящее время неизвестно ни одного алгоритма для вычисления дискретных логарифмов больших чисел за приемлемое время даже на самых быстродействующих компьютерах.

При этом, хотя мы и не можем доказать, что таких алгоритмов вообще не существует, имеется предположение, что модульное возведение в степень (с фиксированным основанием и модулем) действительно является однонаправленной функцией.

Очевидно, что однонаправленные функции не могут непосредственно использоваться в качестве криптосистем (когда m шифруется как f(m)), поскольку тогда даже законный получатель не сможет раскрыть открытый текст! (но они полезны для защиты паролей).

Более употребимым в криптографии является понятие однонаправленной функции с секретом. Функция f: X ® Y называется однонаправленной функцией с секретом, если она может эффективно вычисляться как в прямую, так и в обратную сторону, более того, может быть даже известен эффективный алгоритм вычисления f такой, что полное знание того, как этот алгоритм работает, не дает никакой возможности разработать эффективный алгоритм вычисления обратной ей функции.

Дополнительное знание, с помощью которого могут быть получены оба эффективных алгоритма, как раз и называется секретом.

Пример: строение алгоритма RSA, где число N=p*q, где p и q простые числа и их знание позволяет подбирать открытый и секретный ключи за приемлемое

Вопрос 55.1. Генераторы псевдослучайных последовательностей на основе линейных регистров сдвига (фильтрующие, комбинирующие, с неравномерным движением). Характеристика выходных последовательностей (периоды, линейная сложность, статистические свойства).

Линейный регистр сдвига (ЛРС)

- начальные члены последовательности.

- Преобразование регистра сдвига с обратной связью (Линейное преобразование)

Набор чисел: называется i-ым состоянием регистра сдвига.

Функция 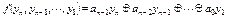- булева функция обратной связи.

- точки съема регистра (номера ячеек, с которых производится съем). j – точка съема ↔ a_j-1=1

Date: 2016-08-30; view: 489; Нарушение авторских прав