Схемы шифрования и подписи RSA

Функция Эйлера:

Открытые сообщения M представляются целыми числами, 1<M<N, где N - большое целое число, равное произведению двух различных больших простых чисел N=P*Q. Алгоритмы шифрования и расшифрования определяются числом N и показателями степени e и d которые связаны соотношением

Шифрование: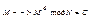

Расшифрование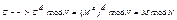

В качестве открытого ключа выступает пара чисел (N, e), а в качестве секретного ключа - число d.

Система электронной подписи RSA получается при "смене мест" ключей e и d.

Подпись сообщения,

проверка подлинности подписанного сообщения [M,S] . Совпадение чисел в левой и правой частях последнего равенства означает, что сообщение M было подписано обладателем секретного ключа d, соответствующего ключу проверки подписи (N, е), т.е. авторизует сообщение.

Для разрешения споров между отправителем и получателем информации, связанных с возможностью искажения ключа проверки подписи (N, E), достоверная копия этого ключа выдается третьей стороне - арбитру и применяется им при возникновении конфликта.

Протокол работы пары абонентов сети общей связи с ОШ алгоритмом RSA выглядит так.

Используя, что сумма примарных колец (основание простое число) равно кольцу произведения оснований, выбираем e такое, что , и находим d, зная p и q.

Абоненты	I	J
Независимо генерируют пары простых чисел	p(i), q(i)	p(j), q(j)
и вычисляют	n(i)=p(i)*q(i), e(i), d(i)	n(j)=p(j)*q(j), e(j), d(j)
Помещают в общедоступный справочник	n(i), e(i)	n(j), e(j)
Сохраняют в секрете	d(i)	d(j)
При обмене сообщениями	M	N
- шифруют и передают
- расшифровывают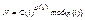
При обмене подписанными сообщениями	M	N
- подписывают, шифруют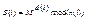
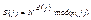
- передают
- расшифровывают
- проверяют подпись

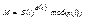
Предполагая, что известны все параметры этого протокола кроме сохраняемых в секрете чисел d(i), d(j) мы должны оценить сложность их восстановления. Если известно разложение на множители числа N=P*Q, то по открытому ключу (N, e), секретный ключ d вычисляется легко.

Поэтому разложение N=P*Q должно также быть недоступным для потенциального злоумышленника. После вычисления пары e, d знание множителей P, Q не нужно даже законным пользователям системы, т.е. они могут быть "забыты". Сложность их определения по числам N, e и является гарантией стойкости системы RSA.

В оригинальной работе RSA авторы предлагали выбрать простые числа P и Q случайно, по 50 десятичных знаков каждое. Через некоторое время было показано, что этого мало, были случаи вскрытия при n=512 (сейчас n³1024).

Правила выбора: n=p*q, , , (p-1) делилось на большое простое число, (p+1) делилось на некоторое другое большое простое число, для q – аналогично. T(RSA<=T(факторизации)).

Date: 2016-08-30; view: 238; Нарушение авторских прав