Теория информации и кодирования

Вопрос 4.1. Количество информации и энтропии. Формулы Хартли и Шеннона

Количество информации и энтропия. Формулы Хартли и Шеннона

Количество информации в дискретном сообщении. Энтропия

Дискретный источник сообщений – источник сообщений, принимающий случайным образом одно из конечного множества возможных состояний U в каждый момент времени. Совокупность состояний u₁, u₂,..,u_i,..,u_N источника называют его алфавитом, а количество состояний N ‑ объемом алфавита. Таким образом, дискретное сообщение – это символ u_i, выдаваемый источником, при этом источник может выдать дискретное сообщение в виде последовательности элементарных дискретных сообщений, представляющей сбой набор символов u_i (например, u₅, u₁, u₃) каждый из которых имеет длительность t_i секунд. Такая модель источника сообщений соответствует реальной ситуации имеющей место в телеграфии (t_i¹const) и передаче данных (t_i=const). В общем случае источник хранится дискретным ансамблем U: ,

При выдаче источником сообщений в виде последовательности элементарных дискретных сообщений, полным вероятностным описанием является вероятность совместного появления набора различных символов u_i в момент t₁, t₂,...,t_n, где n ‑ длина последовательности

.

Располагая такими сведениями об источнике можно вычислить вероятность любого отрезка сообщения длиной меньше n.

Если функция не меняется во времени, т.е. если она при любых t, то источник называется стационарным.

Если при определении вероятностных характеристик стационарного источника усреднение по ансамблю можно заменить усреднением по времени, то такой источник называется эргодическим.

Мера неопределенности источника с равновероятными состояниями и характеризующего его ансамбля U это логарифм объема алфавита источника H(U)=log N (1.1).

Легко видеть, что:

1. с ростом N величина H(U) монотонно возрастает.

2. в случае если объем алфавита источника N равен 1, т.е. когда неопределенность отсутствует, H(U)=log 1=0

3. величина H(U) обладает свойством аддитивности, поскольку log(N*M)=log(N)+log(M).

Впервые данная мера была предложена Хартли в 1928г. Основание логарифма в формуле не имеет принципиального значения и определяет только масштаб или единицу количества информации. Если основание равно 2, то единица количества информации называется двоичной единицей или битом. Если 10, то дитом или хартли. Если же равна е, то натом.

В общем случае, если вероятности различных состояний источника не одинаковы, степень неопределенности конкретного состояния зависит не только от объема алфавита источника, но и от вероятности этого состояния, тогда (1.2). Знак минус в первом равенстве (1.2) необходим для того, чтобы количество информации i(u_k) было неотрицательным числом т.к. всегда P(u_k)£1. Очевидно что, так же как и мера H(U) определяемая (1.1) величина i(u_k) обладает свойством аддитивности. И в случае достоверного сообщения, когда P(u_k)=1, i(u_k)=0. Количество информации в сообщении тем больше, чем оно более неожиданно. Если источник выдает последовательность зависимых между собой элементарных сообщений, то наличие предшествующих сообщений может изменить вероятность последующего, а, следовательно, и количество информации в нем. Оно должно определяться по условной вероятности
P(u_k|u_k-1,u_k-2,…) выдачи сообщения u_k при известных предшествующих сообщениях u_k-1,u_k-2,…, тогда количество информации

Определения (1.2) и (1.3) количества информации являются случайной величиной, поскольку сами сообщения являются случайными. Его распределение вероятностей определяется распределением вероятностей сообщений в данном ансамбле для цифровой характеристики всего ансамбля или источника сообщения используется математическое ожидание количества информации в отдельных сообщениях называемых энтропией или Мерой Шеннона

Свойства энтропии

· Энтропия любого дискретного ансамбля не отрицательна H(U) ³ 0 (1.5).

· Пусть N - объем алфавита дискретного источника, тогда H(U)£ log N (1.6). Равенство имеет место, когда все сообщения источника равновероятные.

· Энтропия объединения нескольких независимых статистических источников сообщений равна сумме энтропии исходных источников ‑ свойство аддитивности энтропии.

При двух сообщениях U и Z можно ввести определение условной энтропии H(U/Z), т.е. появление события U при известном событии Z.

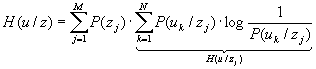, или же

где М{} – мат ожидание.

Условная энтропия удовлетворяет неравенству 0£H(u|z) £H(U), причем H(u|z)=0, когда по реализации ансамбля Z можно точно установить реализацию ансамбля U (канал без помех).H(u|z)=H(U), когда ансамбли U и Z. В общем случае H(u|z)<H(U) и знание реализации Z снижает первоначальную неопределенность U. Отсюда информационная характеристика двух ансамблей U и Z называемая взаимной информацией между U и Z определяется, как

Взаимная информация измеряется в тех же единицах что и энтропия. Величина I(u,z) показывает, сколько в среднем бит информации о реализации ансамбля u дает наблюдение о реализации ансамбля z.

Взаимная информация обладает следующими свойствами:

· I(u,z)³0, причем равенство имеет место только в том случае, когда u и z независимы между собой.

· I(u,z)=I(z,u), т. е. z содержит столько же информации относительно u, сколько u содержит относительно z. Поэтому можно так же записать I(u,z)=H(Z)-H(z|u)

· Причем равенство имеет место, когда по реализации z можно точно восстановить реализацию u или наоборот. Это следует из (1.12) и (1.13). (1.19) вытекает из (1.16) и (1.18).

· Полагая в I(u,z)=H(U)-H(u|z), Z=U и учитывая, что H(u|u)=0, получаем I(u,u)=H(U) Это позволяет интерпретировать энтропию источника как его собственную информацию ансамбля U о самом себе.

· Пусть U ансамбль дискретных сообщений, а Z ансамбль дискретных сигналов, в которые преобразуется сообщение U, тогда I(u,z)=H(U) только в том случае когда преобразование U в Z обратимо, т.е. однозначно. При необратимом преобразовании I(u,z)<H(U) и разность H(U)-I(u,z)=H(u|z) называют потерей информации или ненадежностью преобразования U в Z.

Таким образом, информация не теряется только при обратимых преобразованиях, величина H(z|u)=H(Z)-I(u,z) называется энтропией шума преобразования или ложной информацией, создаваемой при образовании.

Date: 2016-08-30; view: 481; Нарушение авторских прав