
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Случайность во времени 3 page
|
|
Согласно математической теории, на которой базируется построение звукоряда люй, хуан чжун в качестве седьмой ступени от тоники жуй бинь имеет числовое выражение 729/512 @ 1,424. Это число достаточно близко дроби 10/7 @ 1,429, на основе которой строится эннеаграмма (точнее, декаграмма), и числу Ö 2 @ 1,414, являющемуся среднегеометрическим для чисел 1 и 2, определяющих диапазон октавы.
С помощью квинтового хода от тоники жуй бинь выстраивается полный триграммный порядок A2 (см. рис. 2.6.6; ср. табл. 2.2.1). Причем, между ним и полным триграммным порядком “взаимопорождения” (A3) обнаруживается “музыкально-математическая” связь по принципу звезды, подобная представленной в традиционной теории стихий сокращенной связи между порядками “взаимопреодоления” (А1) и “взаимопорождения”.
Связь триграмм в порядке “взаимопорождения” со звукорядом люй позволяет интерпретировать ступени последнего в триграммных характеристиках. Таким образом, музыкальные звуки могут рассматриваться как средство коммуникации между Небом и Землей, любыми субъектом и объектом, находящимися в состоянии “могущества” и “послушности” (см. табл. 2.1.8). Последние понятия связаны на базис-схеме соответственно со ступенями тоники (c -111) и октавы с малой секундой (cis -000). Остальные ступени будут выражать музыкальные “посылы”, определяемые свойствами “младших” триграммам: секунда(d) — “одаривание” (110); терция(e) — “процветание” (101); ув. кварта (fis)—“сдерживание” (100); квинта (g) — “благодарение” (011); секста(a) — “упадок (выдержка)” (010); септима (h) — “возбуждение” (001). Эти “коммуникативные архетипы” могут варьироваться в зависимости от различных взаимоотношений триграмм, о которых пойдет речь в последующих главах. Поскольку “младшие” триграммы охватывают по две рядом стоящие ступени, их характеристики относятся и к тем соответствующим им ступеням, которые не вошли в рассматриваемый перечень.
Если в качестве тоники взять не жуй бинь, а ступень линь чжун (сis), которая определяет начало порядка “взаимопорождения” только для “младших” триграмм, то хуан чжун снова займет срединное положение в октаве. При этом в системе люй обнаружится некоторое сходство с древнегреческим музыкальным строем, который ведет свое начало от Пифагора (580—500). Согласно позднеантичному автору Гауденцию, в музыкальной теории пифагорейцев фундаментальное положение имела четверка чисел 12, 9, 8, 6, соотносимая на монохорде с длиной целой струны (12/12 = 1) и ее частями (9/12 = 3/4; 8/12 = 2/3; 6/12 = 1/2) (см.: Ван-дер-Варден 1959: 133). При длине струны, рассматриваемой в качестве тоники и равной 12 единицам, число 9 выражает интервал кварты, 8 — квинты, 6 — октавы. Между звуками с числами 9 и 8 при этом устанавливается интервал, равный тону. Число 9 обозначало у греков ступень, называвшуюся месой (“средняя”) и выполнявшую функцию центра тяготения для всех других нот октавного звукоряда. Все эти ноты можно получить последовательными квинтовыми ходами от месы, сводя их по мере надобности в пределы октавы.
Такую же функцию выполняет “срединная” ступень хуан чжун в звукоряде, начинающемся с линь чжун. Эта ступень традиционно связывается с числом 9, из которого получаются числа 8 и 6 для ступеней, находящихся выше хуан чжуна на тон и квинту (см. табл. 1.4.4). Если построить кварту вниз от хуан чжуна, то она выразится числом 12. Что касается всего звукоряда люй, то, как многократно указывалось ранее (см., например, табл. 1.4.2), он традиционно выстраивается от хуан чжуна посредством череды квинтовых ходов. “Срединность” хуан чжуна в этом случае можно выразить двояко. Если восходящую октаву обозначать числами 12 и 6, то число 9, связанное с хуан чжуном, определится как их среднеарифметическое [9 = (12 + 6)/2]. Если взять обратные величины от 12 и 6 — 1/12 и 1/6, что будет равносильно смещению внимания от длин к частотам колебательных объектов, то число 1/9 определится как среднегармоническое указанных октавных чисел [1/9 = 2/(1/1/12 + 1/1/6) = 2/(12 + 6)].
Анализ звукоряда с выявлением среднеарифметической и среднегармонической величин был свойствен грекам и не проводился, насколько известно по историческим документам, древними китайцами, однако, не в этом суть. В обоих случаях речь шла о звукоряде, который строится квинтовым ходом, и в этом звукоряде выделялась средняя ступень. На первый момент уже давно обращалось внимание исследователями. Сходство заставляло думать о генетической связи. Э. Шаванн, например, считал, что пифагоров строй был занесен экспедицией Александра Македонского в завоеванные им восточные страны, а из них через Памир проник и в Китай. Дж. Нидэм подверг критике данное мнение, указывая на более раннее происхождение китайской системы люй по сравнению с пифагоровым строем, и выдвинул гипотезу о “вавилонском источнике”, из которого заимствовали музыкально-теоретические знания как греки, так и китайцы (см.: Needham 1962: 176—183). Доводов, по сути, было два: древность шумеро-вавилонской цивилизации и центральность ее положения относительно Греции и Китая. В отношении музыкально-теоретических знаний этого “источника” он ничего не говорит, что и не удивительно, поскольку до сих пор исследователями не обнаружено сколько-нибудь значимое выражение таковых. Еще одна точка зрения по данному вопросу принадлежит А. Гладишу. Согласно М. Уэсту, в серии книг, первая из которых была опубликована в 1841 г., этот автор доказывал, что Пифагор заимствовал свое учение у китайцев, Ксенофан и элеаты — у индийцев, Эмпедокл — у египтян, Анаксагор — у евреев (West 1971: 166). От комментариев ко всему этому списку лучше воздержаться. Однако в отношении учения Пифагора, видимо, следует признать правоту А. Гладиша, разумеется, если учитывать наличие посредников. К такому мнению заставляют склониться не только отмеченные сходства (о дополнительных сходствах см.: Еремеев 1996: 21—28), но и характеристики китайского звукоряда люй. Если при своем формировании звукоряд люй и мог испытывать внешние влияния, пусть даже из Месопотамии, то в сформированном виде он стал неотъемлемой частью арифмосемиотики, о привнесении которой в Китай говорить не приходится, и приобрел такую высокую степень организованности, которая не была достигнута нигде в древнем мире, но бледные следы которой можно увидеть в учении Пифагора.
Триграммный код
Арифмосемиотическая сторона учения о 12-ти люй более всего проступает в контексте теории триграмм. Как уже указывалось (см. рис. 2.6.6), на базис-схеме с триграммами в порядке “взаимопорождения” музыкальный звукоряд в целом образует интервал октавы с малой секундой, что составляет 6,5 тонов. Важно подчеркнуть, что при этом триграммы можно рассматривать не просто символами соответствующих ступеней, а их кодами со структурой, определяющей величину кодируемой ступени.
Для кодирования должны быть использованы интервалы квинты, большой терции и секунды. Квинта является интервалом, на основе которого строится звукоряд из 12-ти люй. Секунда образуется в результате сочетания двух квинт, сведенных в одну октаву. Что касается большой терции, то о знакомстве с ней древних китайцев можно судить по названиям нот системы люй. Если не считать ноты хуан чжун, то остальные три ноты, в названия которых входит иероглиф чжун (“колокол”), находятся друг от друга на интервалах, равных большой терции. То же самое относится и к трем нотам, в названия которых входит иероглиф люй (“флейта”) (см. табл. 2.6.1).
Итак, если позициям X, Y, Z поставить в соответствие интервалы квинты (3,5 тона), большой терции (2 тона) и секунды (1 тон), обозначаемые янскими знаками (1), то для каждой триграммы сумма янских знаков будет соответствовать количеству тонов, на которое ступень, символизируемая этой триграммой, отличается от ступени, символизируемой принятой за точку отсчета триграммой Кунь (000). Подобную кодировку можно применить и для иньских знаков (0), взяв за начало отсчета триграмму Цянь (табл. 2.6.3).
X. Квинта — 3,5 тона;
Y. Б. терция — 2 тона;
Z. Секунда — 1 тона.
| Таблица 2.6.3 | |||
| Код | Янский интервал от 000 (в тонах) | Иньский интервал от 111 (в тонах) | Нота |
| 3,5 + 2 + 1 = 6,5 | c | ||
| 3,5 + 2 = 5,5 | d | ||
| 3,5 + 1 = 4,5 | e | ||
| 3,5 | 2 + 1 = 3 | fis | |
| 2 + 1 = 3 | 3,5 | g | |
| 3,5 + 1 = 4,5 | a | ||
| 3,5 + 2 = 5,5 | h | ||
| 3,5 + 2 + 1 = 6,5 | cis |
Выделенные квинтовым ходом ступени с “младшими” триграммами совпадают с эннеаграммными (точнее, додекаграммными) узловыми точками, на которых строится гексанема с “ротационным” (G) порядком. В додекаграмме, как указывалось выше (см. рис. 2.2.7), она объединяет числа, которые входят в периодическую дробь 12/7 = 1,[8|6|10|3|5|1], выраженную в двенадцатеричном счислении (рис. 2.6.7).
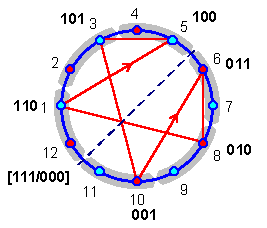
Рис. 2.6.7
Числовой порядок в данной фигуре сдвинут на одну единицу вперед относительно обозначения месяцев в китайском сельскохозяйственном календаре. Однако при выборе 12-ти частей круга для деления на число 7 нумерация этих частей будет совпадать с календарной.
Ранее было показано преобразование по гексанеме триграммных порядков (см. рис. 2.2.4; 2.2.9). В данном случае это преобразование можно конкретизировать привязкой к узловым точкам додекаграммы и ступеням звукоряда люй (рис. 2.6.8).

Рис. 2.6.8
Получившиеся порядки триграмм будут символизировать звукоряды с различными музыкальными интервалами — большими и малыми секундами, секстами, септимами, терциями и чистыми квинтами и квартами. Для наглядности все их можно изобразить на базис-схеме с круговым порядком “взаимопорождения” (А3), который сам является звукорядом с последовательностью шести больших и одной малой секунд (рис. 2.6.9).

Рис. 2.6.9
Семеричный цикл
Триграммы создавались как квазиуниверсальные символы и призваны символизировать различные циклы. Было показано, что на круговой схеме они могут символизировать шестеричный цикл за счет исключения “старших” триграмм и восьмеричный цикл за счет соотнесения со звукорядом, имеющим в случае порядка “взаимопорождения” диапазон в октаву с малой секундой. Триграммы также могут символизировать семеричный цикл, в котором, во-первых, триграмма Кунь (000) обозначает ту же самую фазу цикла, что и Цянь (111), но только на новом витке, и, во-вторых, сам цикл является октавным для порядка “взаимопорождения”. Получение других порядков в таком случае также может производиться с помощью перемещения символов триграмм по гексанеме. Кроме того, возможно еще преобразование порядков по семилучевой звезде, когда триграммы в порядке по звезде последовательно переставляются в порядок по кругу (рис. 2.6.10).

Рис. 2.6.10
Чтобы восемь триграмм укладывались таким образом в октавный круг, необходимо изменить кодировку их позиций следующим образом:
X. Условная квинта @ 1,486 < 3,5 тона;
Y. Условная б. терция @ 1,219 < 2 тона;
Z. Условная секунда @ 1,104 < 1 тона.
В темперированном строе 12 квинт составляют интервал в 7 октав, а в пифагоровом — чуть больший. Чистая квинта равна 3/2 = 1,5, а темперированная — приблизительно 1,498. Условная квинта образуется при делении круга на число 7, и 7 таких квинт составят 4 октавы.
Порядки А1, А2 и А3 можно представить в одной таблице (табл. 2.6.4), которая показывает принцип их преобразований, заключающийся в дихотомическом делении, подобном тому, что применяется при получении триграмм и гексаграмм из Великого предела. Этот принцип позволяет добавить в таблицу неограниченное количество столбцов справа и слева от имеющихся, что делает ее сходство со схемой Великого предела еще более очевидным.
| Таблица 2.6.4 | ||
| A2 | A1 | A3 |
| 000/111 | 000/111 | 000/111 |
| 000/111 | ||
| 000/111 | 000/111 | |
| 000/111 | ||
| 000/111 | 000/111 | 000/111 |
Другая аналогия, на которую здесь уместно указать, — это метод фракталов, или масштабного автоподобия. Взяв какой-либо триграммный порядок, через три шага преобразований можно получить тот же самый порядок, но масштабно уменьшенный или увеличенный. Так, если в качестве исходного берется порядок “взаимопорождения” (А3), который символизирует октаву, т.е. диапазон от 1 до 2, то этот же самый порядок при уменьшении будет символизировать диапазон от 1 до приблизительно 1,104, а при увеличении — от 1 до 128, что составляет точно 7 октав (табл. 2.6.5).
| Таблица 2.6.5 | |||
| A3 | Уменьшение | Норма | Увеличение |
| 20 = 1 | |||
| 1,014... | 1,104... | 21 = 2 | |
| 1,029... | 1,218... | 22 = 4 | |
| 1,043... | 1,345... | 23 = 8 | |
| 1,058... | 1,485... | 24 = 16 | |
| 1,073... | 1,639... | 25 = 32 | |
| 1,088... | 1,810... | 26 = 64 | |
| 1,104... | 27 = 128 |
“ Порождающая” октава
“Порождающая” роль октавного диапазона заключается в том, что он, с точки зрения математической символики, является производным от единицы и производящим единицу. Можно сказать, что октавный переход от 1 к 2 (= 1 + 1) или от 1 к 1/2 (= 1/1 + 1) — это появление новой единичной сущности, копируемой по первичному эталону. Если полагать этот эталон вне сферы явлений, поскольку первоначально, будучи не сравним ни с чем, он как бы и не существует, то развитие октавы можно определить как становление бытия.
В музыке октава — установление наиболее консонансного звука, а с точки зрения психологии восприятия — появление нового качества, для которого задан прототип. В акустике октава рассматривается как удвоенное увеличение частоты, уменьшение периода колебаний некоего вибратора или уменьшение вдвое его длины. Иначе говоря, октава здесь рассматривается в категориях времени и пространства и представляет собой установление единиц их измерений.
Соотнесенность октавы с порядком “взаимопорождения” триграмм или стихий можно рассматривать в контексте древнекитайской картины мира как установление пространственно-временного континуума между Небом и Землей (см. табл. 2.3.9). Увеличивающийся по высоте вибраций поток энергии спускается от Неба к Земле, насыщая ее своей благодатной силой. Триграммы или стихии в порядке “взаимопорождения”, выраженные посредством музыкальных ступеней, — это как бы этапы такого нисхождения. Повышение частоты вибрации сопровождается понижением ее длины волны, поскольку между частотой и длиной волны имеется обратно пропорциональная зависимость, которую можно уподобить взаимоотношениям сил ян и инь, “являющихся корнями друг друга”. Музыкальный звукоряд люй прекрасно отражает этот дуализм (рис. 2.6.11).

Рис. 2.6.11
Уравновешенность частоты и длины волны колебаний наблюдается на 7-й ступени, коррелирующей по реконструкции с хуан чжуном (см. рис. 2.6.6) и тем самым позволяющей еще раз утверждать о его срединности. В порядке “взаимопорождения” данный пункт совпадает с фазой кульминации описываемого этим порядком процесса, c окончанием действия триграммы Гэнь и стихии “почва”. После этого, хотя частота энергетической волны продолжает возрастать, в развитии системы, описываемой циклом триграмм или стихий, наступает спад. С этого момента данное описание можно перевести с регистрации изменения частотных характеристик на регистрацию характеризующего данный процесс изменения длины волны, что является очередным переключением с ян на инь, и если в первом полупериоде будет фиксироваться рост частоты, то во втором — убывание длины волны, причем математические выражения этого роста и убывания будут симметричны.
С другой стороны, симметричность относительно данного пункта прослеживается и в наборе величин, выражающих только один из параметров октавной шкалы, будь то частота колебаний, их период или длина волны. Геометрическим средним чисел 1 и 2, задающих октавное отношение, является Ö 2 (b = Ö 2 в формуле a/b = b/c, при a = 1 и c = 2), что, как показывалось выше, близко значению реконструированного хуан чжуна. Таким образом, система люй рассекается на две части, элементы которых могут быть выражены дробями с симметричными числителями и знаменателями.
Трехмерные вибрации
В проводившейся выше реконструкции было показано, что “космогонический” порядок представляет собой более дробное описание полупериодов порядка “взаимопорождения” (см. рис. 2.2.14), получаемое за счет операции симметризирования. В китайской арифмосемиотике “космогонический” порядок через пентатонику связывается с октавой (см. табл. 1.3.1, 1.4.6, 1.4.8). То, что порядок “взаимопорождения” сам состоит из октавы, заставляет предполагать, что для получения из него “космогонического” порядка эта октава должна быть преобразована в две октавы, что легко достигается путем возведения во вторую степень величин всех ее ступеней. После этого вторая октава должна быть инвертирована. Таким образом, порядок “взаимопорождения” будет коррелировать с комплексом из восходящей и нисходящей октав, которые вместе образуют замкнутую цепочку чисел с полюсами, имеющими значения 1 и 2. При образовании из порядка “взаимопорождения” обратного “космогонического” порядка (110—001—101—010—100—011) он будет соотноситься со звукорядом 12 люй, являющимся, так же как и в традиционной корреляции, восходящим, но только имеющим сдвинутую тонику (рис. 2.6.12).

Рис. 2.6.12
На основании “космогонического” люй можно построить пентатонику, учитывая традиционные корреляции нот и стихий (рис. 2.6.13). При этом тоника- гун этой пентатоники окажется на месте, ничем не примечательном, и можно предположить, что в древности упор делался на другую ноту (например, шан, которая является средней в квинтовой структуре пентатоники). С другой стороны, примечательным оказывается то, что при построении пентатоники в таком ракурсе не используется стихия “вторичное дерево” (Д*), которая не присутствовала и в известных традиционных музыкально-стихийных конструкциях.

Рис. 2.6.13
“Космогонический” (C3) порядок триграмм получается за счет преобразования порядка “взаимопорождения” (A3), а он — “ротационного” (R). При этом первые два порядка накладываются на третий. Можно сказать, что все вместе образуют некую трехмерную конструкцию, свойства которой оказываются присущи и звуковысотным последовательностям, символизируемым данными порядками. Одна такая последовательность представляет собой изменение частоты колебаний, действующих в одном измерении и распространяющихся как волна в другом. Соединение двух последовательностей — это колебания в двух измерениях, которые можно представить в виде спирали, “ввинчивающейся” в третье измерение. Наконец, три последовательности дадут нам достаточно странное образование. Колебания в трех измерениях создают некую объемную фигуру, а именно трехмерную фигуру Лиссажу. Можно сказать, что таким образом возникает вибрационная “заузленность” или солитоноподобный квант. Такой квант будет фиксированным при определенных постоянных величинах трех колебаний, из которых он состоит. Но в звукорядах, символизируемых тремя триграммными порядками, происходит последовательное изменение высотных характеристик при переходе от ступени к ступени. Значит и данный квант также должен двигаться, попутно изменяя свои параметры.
Эта модель сложения трех колебательных систем интересна тем, что с ее помощью можно внести важный штрих в древнекитайскую космологию. Ведь колебания, описываемые в теории люй, — это колебания энергодинамической субстанции, называемой китайцами ци. Она по своей природе является континуальной, но на конкретных уровнях мироздания может пребывать как достаточно устойчивые дискретный образования, неделимые далее в пределах соответствующего уровня. Эти устойчивые образования пневмы- ци и можно уподобить кванту, состоящему из трех колебаний, символизируемых “ротационным”, “взаимопорожденческим” и “космогоническим” триграммными порядками. Понятно, что диапазон этих колебаний не обязательно должен соответствовать звуковому. 12 люй просто являют собой некий структурный образец, который можно перенести в любой диапазон любых вибраций. Можно добавить, что кванты пневмы- ци, лежащие в основе мироздания, с виду напоминают “кирпич” со сторонами, находящимися в отношении 1, 2 и 4. Ведь такие же отношения имеют колебательные системы, символизируемые тремя связанными триграммными порядками.
“ Музыкальный” порядок Фуси
Если порядок “взаимопорождения” (A3) представляет собой движение с Неба на Землю, то порядок Фуси (B1) по своей сути является обратным движением. В древнекитайской арифмосемиотике не сохранилась его корреляция с музыкальным звукорядом, но она крайне необходима для полноты системы.
Триграммы, расположенные в порядке Фуси, представляют собой зеркальные отражения триграмм в порядке “взаимопорождения”. Поэтому, чтобы использовать порядок Фуси в качестве кодировки музыкальных ступеней, необходимо зеркально переставить соответствия позиций триграмм и интервалов.
X. Секунда — 1 тон;
Y. Б. терция — 2 тона;
Z. Квинта — 3,5 тона.
При такой кодировке учитываются только интервалы между ступенями, но не учитывается направление звукоряда. Исходя из идеи противопоставления всего по принципу ян—инь, звукоряд для порядка Фуси, в отличие от порядка “взаимопорождения”, должен быть нисходящим по высоте (табл. 2.6.6).
| Таблица 2.6.6 | |||
| Код | Янский интервал от 000 (в тонах) | Иньский интервал от 111 (в тонах) | Нота |
| 1 + 2 + 3,5 = 6,5 | c | ||
| 2 + 3,5 = 5,5 | b | ||
| 1 + 3,5 = 4,5 | gis | ||
| 3,5 | 1 + 2 = 3 | fis | |
| 1 + 2 = 3 | 3,5 | f | |
| 1 + 3,5 = 4,5 | dis | ||
| 2 + 3,5 = 5,5 | cis | ||
| 1 + 2 + 3,5 = 6,5 | h |
Если небесные силы китайцы считали творческими, и это творчество осуществляется в порядке “взаимопорождения” как восходящий звукоряд, то земные силы, будучи силами исполнения и подчинения, должны выражаться, во-первых, в зеркальном “взаимопорождению” порядке, т.е. в порядке Фуси, и, во-вторых, как нисходящий звукоряд, поскольку, с музыкально-акустической точки зрения, восхождение по звукоряду представляет собой увеличение энергии колебаний, а нисхождение — ее уменьшение, что можно рассматривать соответственно как негэнтропийный и энтропийный процессы. На основе нисходящего звукоряда, символизируемого порядком Фуси (В1) и охватывающего октаву с малой секундой, можно построить звезду с незамкнутыми двумя лучами, которая объединит все триграммы, связав их с обозначенными кодом звуковысотными значениями (см. табл. 2.6.6). Лучи в данном случае будут выражать не квинтовые, а квартовые интервалы. Все вместе они будут соответствовать порядку триграмм В2 (рис. 2.6.14; ср. рис. 2.6.6, табл. 2.2.1).

Рис. 2.6.14
Приводившиеся выше рассуждения относительно музыкально-акустических закономерностей порядка “взаимопорождения” и производных от него порядков справедливы с соответствующей перестановкой некоторых моментов и в отношении порядка Фуси и его производных, и поэтому здесь нет смысла останавливаться на их детальном анализе. Более интересно будет рассмотреть другие закономерности на примере “современного” порядка, выводимого из Фуси.
“ Музыка” циркуляции пневмы
Обратный “современный” порядок триграмм (011—100—101—010—001—110), составляющий основу схемы циркуляции пневмы- ци по меридианам, также будет связан с нисходящим октавным звукорядом, который можно получить в результате возведения в квадрат ступеней, коррелирующих с первым полупериодом порядка Фуси, или просто за счет переворачивания октавного звукоряда, символизируемого “космогоническим” порядком, по оси, проходящей через ступени хуан чжун (fis) и жуй бинь (с) (рис. 2.6.15, ср. рис. 2.6.6, 2.6.12, 2.6.13, 2.6.14).

Рис. 2.6.15
Ранее, при реконструкции триграммной схемы циркуляции пневмы по меридианам (см. рис. 2.3.6—2.3.10), в отношении местоположения “старших” триграмм предполагалось, что они просто стоят рядом с коррелирующими с ними посредством стихий “младшими” триграммами: Цянь (111) — с Дуй (011), а Кунь (000) — с Гэнь (100). Тем самым они должны обозначать некоторые управляющие структуры человеческого организма, представленного посредством данной схемы. Теперь, учитывая “музыкальный” характер связи между этими триграммами, можно сделать некоторые уточнения.
Как выяснилось в настоящей главе, в порядке Фуси триграмма Цянь (111) по звуковысотному отношению выше на один тон триграммы Дуй (011), а Кунь (000) — ниже также на один тон триграммы Гэнь (100) (см. табл. 2.6.7, рис. 2.6.14). При преобразовании порядка Фуси в “современный” методом симметризирования (см. рис. 2.2.15; 2.3.10) триграмма Дуй остается неподвижной, а Гэнь меняет свое местоположение. При этом также меняется и ее звуковысотное определение, и у триграммы Дуй оно также поменяется, но их звуковысотные отношения со “старшими” триграммами должны сохраниться если не в конкретных величинах, то, по крайней мере, по характеру. Соответственно триграмма Цянь должна отстоять на круговой схеме от триграммы Дуй на некоторый интервал по направлению против часовой стрелки, а триграмма Кунь от триграммы Гэнь — по часовой стрелке (см. рис. 2.6.15).
Эти интервалы совпадают с местоположением двух из трех управляющих эннеаграммных чисел (3, 6, 9), связь которых с “современным” порядком была установлена при анализе схемы Ло шу (см. рис. 2.5.12; 2.5.22). Как было показано, числа эннеаграммы на схеме с “современным” порядком триграмм можно сдвигать по кругу с шагом, равным числу 3. Кроме того, они могут располагаться на этой схеме в прямом и обратном направлениях по отношению к ходу времени. Главное, чтобы при этом выполнялось правило соотнесения чисел 3, 6 и 9 с управляющими структурами описываемого данной схемой человеческого организма. На рис. 2.6.15 указан только один из шести вариантов их местоположения (средний ряд чисел на рис. 2.5.22).
Date: 2016-08-30; view: 364; Нарушение авторских прав