Постановка задачи дискретного программирования

Под задачей дискретного программирования (ДП) понимается целочисленная задача, в которой все или некоторые переменные должны принимать не любые целые значения.

Особый интерес к задачам ДП вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных. Например, мебельная фабрика выпускает диваны, кресла и стулья. Требуется определить, сколько можно изготовить спинок диванов, подлокотников кресел и ножек стульев, если для их изготовления требуются заданные ресурсы, чтобы доход был максимален. При этом следует иметь ввиду, что выпуск спинок может принимать любое целое значение, подлокотники изготавливаются парами, а ножки должны быть кратными четырем.

Рассмотренную задачу распределения ресурсов с учетом требования дискретного значения переменных в общем виде можно записать так:

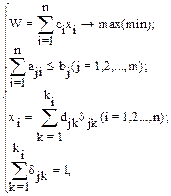
где

d_i1, d_i2,..., d_ik - дискретные значения, которые может принимать переменная x_i.

d_i =

Данная постановка отличается от задачи распределения ресурсов линейного программирования

появлением булевых переменных и увеличением числа ограничений. На практике к задачам с булевыми переменными можно свести значительное число самых различных задач. Там, где есть варианты, из которых надо выбирать, задачу можно решать с помощью булевых переменных.

Выделяют два метода решения задач с булевыми переменными:

1. Метод полного перебора. Алгоритм метода заключается в следующем:

· в специальной таблице заполняются все варианты сочетаний значений d₁, d₂,..., d_k;

· определяются значения левых частей ограничений и целевой функции и записываются в таблицу;

· вычеркиваются варианты, в которых нарушается по крайней мере одно ограничение;

· из оставшихся вариантов принимается тот, в котором целевая функция принимает максимальное (минимальное) значение.

2. Решаются как обычные задачи целочисленного программирования, т.е. методом ветвей и границ. При этом на каждую переменную накладывается два ограничения: они должны быть в пределах 0£d_i£1; d_i должны быть целыми.

Date: 2016-07-25; view: 1344; Нарушение авторских прав