
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение задач линейного программирования на ЭВМ
|
|
Задачи линейного программирования могут быть решены с использованием многих пакетов прикладных программ, а именно:
· Statgraphics;
· LINDO;
· LINGO;
· MathCAD;
· Mathematica;
· MS Excel.
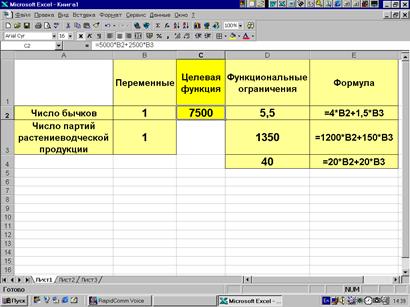
Рис. 9.2.
В качестве примера рассмотрим решение задачи примера 2.1 с использованием MS Excel. Для определенности в ячейки B1:B2, C1 и D1:D3 введем соответственно некоторые начальные значения двух переменных, целевую функцию и левые части функциональных ограничений. При этом необходимо переприсвоить значения x1 на B2 и x2 на B3 (рис. 9.2). Поиск осуществляется с помощью процедуры "поиск решения", которая вызывается из меню "сервис" (рис. 9.3). В появившемся окне (рис. 9.4) необходимо ввести:
· В поле "Установить целевую" введите ссылку на ячейку, содержащую целевую функцию (С1).
· Введите искомый результат в поле "Равной" (максимальное значение прибыли).
· В поле "Изменяя ячейки" введите ссылки на ячейки, содержащие переменные (B2:B3).
· В поле "Ограничения" введите с помощью кнопок "добавить", "изменить" и "удалить" ввести функциональные и областные ограничения.
· С помощью кнопки "Выполнить" запускаем процедуру на выполнение.
Результаты расчетов представлены на рис. 9.5.
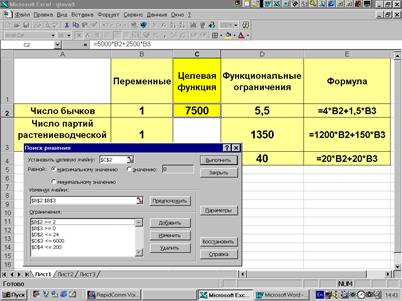
Рис. 9.3.
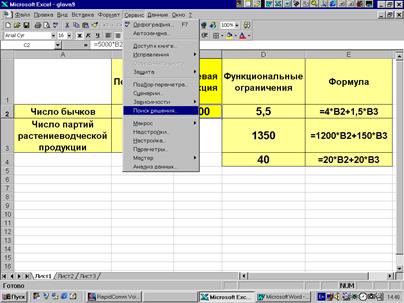
Рис. 9.4.
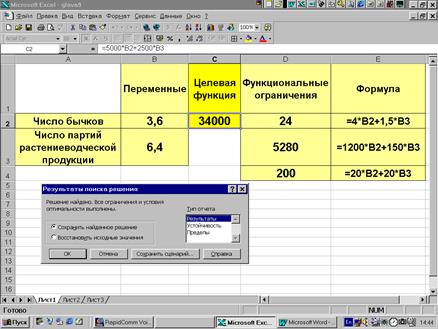
Рис.9.5.
Контрольные вопросы и задания
1. Приведите математическую формулировку основной задачи линейного программирования.
2. Какие неизвестные ограничения системы называются базисными?
3. В чем заключается основная идея симплекс-метода?
4. В чем состоит различие между симплекс-методом и методом полного перебора допустимых вершин области, задаваемой ограничениями?
5. Каковы содержание и последовательность шагов симплекс -алгоритма, реализуемого на симплекс-таблицах?
6. Как при помощи симплекс-метода определить, что задача линейного программирования имеет неограниченный оптимум?
7. Что такое искусственные переменные и для чего они служат? В чем их отличие от остаточных (избыточных) переменных?
8. Что такое анализ чувствительности и для чего он применяется?
9. Фирма выпускает три продукта: A, B, C. На производство единицы продукта A требуется затратить 1 ч. труда ИТР, 10 ч. физического труда и 3 кг сырья. Для единицы продукта B соответствующие показатели равны 2 ч., 4 ч и 2 кг, для продукта C - 1 ч, 5 ч. и 1 кг. Ресурсы составляют 100 ч. труда ИТР, 700 ч. физического труда и 400 кг сырья. При оптовых закупках покупателю предоставляются скидки, так что прибыли от продажи продукции изменяются, как показано в табл. 2.12. Например, если продается 120 ед. продукта A, то первые 40 ед. приносят по 10 руб. прибыли; следующие 60 - по 9 руб., а остальные 20 - по 8 руб. Сформулируйте задачу линейного программирования, решение которой определяет наиболее доходный производственный план.
Таблица 9.12.
| Продукт А | Продукт B | Продукт C | |||
| Прода-жа, ед. | Удельная прибыль, руб. | Прода-жа, ед. | Удельная прибыль, руб. | Прода-жа, ед. | Удельная прибыль, руб. |
| 0-40 | 0-50 | 0-100 | |||
| 40-100 | 50-100 | Более 100 | |||
| 100-150 | Более 100 | - | - | ||
| Более 150 | - | - | - | - |
10. Леспромхоз, имеющий лесопильный и фанерный цеха, столкнулся с проблемой наиболее рационального использования выделенной лесосеки. Чтобы получить 2,5 м3 коммерчески реализуемых комплектов пиломатериалов, необходимо израсходовать 2,5 м3 еловых и 7,5 м3 пихтовой древесины. Для изготовления 100 м2 фанеры требуется 5 м3 еловых и 10 м3 пихтовой древесины. Выделенная лесосека содержит 80 м3 еловых и 180 м3 пихтовой древесины. Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10 м3 пиломатериалов и 1200 м2 фанеры. Доход с 1 м3 пиломатериалов составляет 80 000 руб., а со 100 м2 фанеры - 300 000 руб. Оптимизировать использование лесосеки.
11. Мебельное предприятие выпускает три вида наборов мебели, книжные полки и тумбу под телевизоры. Характеристики каждого вида продукции приведены в табл. 9.13. При условии получения максимальной прибыли объем товарной пилопродукции должен составить не менее 459 310 тыс. руб. Ситуация со сбытом продукции сложилась следующая. Книжными полками рынок насыщен, поэтому торговые организации уменьшили объем договоров до 10 тыс. шт. Тумбы для телевизоров могут быть реализованы в объемах от 4 до 7 тыс. шт., наборы мебели 2 - от 7 до 10 тыс. шт. Спрос на наборы мебели 1 и 3 неограничен и требуется не менее 10 тыс. шт. Предприятие имеет технологическое оборудование, число единиц которого и нормы затрат времени оборудования каждой группы на изготовление единицы каждого вида продукции приведены в табл. 9.14. Предприятие работает в две смены с эффективным временем работы каждой машины в 3945 ч. (коэффициент сменности 1,9). Оптимизировать производственную программу предприятия.
Таблица 9.13.
| Виды продукции | |||||
| Показатель | Набор мебели 1 | Набор мебели 2 | Набор мебели 3 | Книжные полки | Тумба |
| Оптовая цена, тыс.руб | |||||
| Прибыль от реализации, тыс. руб |
Таблица 9.14
| Виды продукции | ||||||
| Наименование оборудования | К-во, шт. | Набор | Набор | Набор | Полки | Тумба |
| Линия раскроя | 0,068 | 0,096 | 0,207 | 0,018 | 0,042 | |
| Гильотинные ножницы | 0,045 | 0,080 | 0,158 | 0,011 | 0,035 | |
| Линия облицовывания | 0,132 | 0,184 | 0,428 | 0,020 | 0,060 | |
| Линия обрезания кромок | 0,057 | 0,082 | 0,230 | 0,010 | 0,028 | |
| Лаконаливная машина | 0,063 | 0,090 | 0,217 | 0,010 | 0,032 | |
| Полировальные станки | 0,170 | 0,280 | 0,620 | 0,020 | 0,096 |
12.В леспромхозе производится раскряжевка хлыстов на сортименты. Требуется получить сортименты трех видов - длиной 6, 2,2 и 1,5 м. Длина среднего хлыста 31 м, средний диаметр 0,3 м. План поставки сортиментов, соответственно, 30000 м3, 86000 м3 и 40000 м3. Используя карту раскроя хлыстов без учета толщины пропила и сбега (табл. 9.15) определить оптимальный план раскроя.
Таблица 9.15
| Сорти- | Варианты раскроя хлыстов | ||||||||||
| мент, м | |||||||||||
| 2,2 1,5 | |||||||||||
| Отходы | 1,1 | 0,3 | 0,5 | 1,0 | 1,2 | 0,3 | 0,7 | 1,1 | 0,3 |
13. Нижний склад производит два вида продукции: обрезную доску и брус. Для изготовления 1 м3 бруса требуется 2,5 м3 сосны или 3 м3 ели. Для изготовления 1 м3 доски требуется 3 м3 сосны или 3,5 м3 ели. Максимальные суточные запасы сосны - 200 м3, ели - 300 м3. Суточный спрос на брус - 100 м3, на доску - 150 м3 при оптовых ценах за 1 м3 бруса - 200 000 руб., за 1 м3 доски - 300 000 руб. Определить оптимальные объемы выпуска бруса и доски.
14. Лесхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не менее 6 единиц вещества A и 12 единиц B. Какое количество корма надо расходовать ежедневно на одного животного, чтобы затраты были минимальны (по данным табл. 9.16)?
Таблица 9.16
| Питательные вещества | Количество питательных веществ в 1 кг корма вида: | |
| A B | ||
| Цена 1 кг, руб |
15. В деревообрабатывающий цех завода поступил заказ вырезать из фанеры заготовки двух видов для 1000 изделий. Известно, что на одно изделие идет 2 заготовки первого вида и 3 - второго. Существуют три способа раскроя: при первом способе из листа фанеры получается 5 заготовок первого вида и 2 заготовки второго вида, при втором: 1 заготовка первого вида и 2 заготовки второго и при третьем - соответственно 3 и 4. Сколько листов фанеры следует раскроить по каждому способу, чтобы выполнить заказ и свести расход фанеры до минимума?
16. Леспромхоз имеет древесину трех видов в количествах: 1 - 1000 м3, 2 - 500 м3, 3 - 700 м3, для изготовления изделий A, B, C и D. Нормы расхода древесины в м3 на изготовление единицы каждого изделия и прибыль от реализации единицы изделия даны в табл. 9.17. Определить, сколько изделий каждого вида должно произвести предприятие, чтобы общая прибыль от реализации всех изделий была максимальной?
Таблица 9.17
| Сырье | Нормы расхода сырья на единицу изделия | |||
| A | B | C | D | |
| 0,1 0,2 0,4 | 0,15 0,4 0,5 | 0,2 0,3 0,1 | 0,25 0,1 0,2 | |
| Прибыль, руб |
17. Производство двух видов лесопродукции должно пройти три операции. Затраты времени на каждую операцию на изготовление одного изделия, прибыль от реализации одного изделия представлены в табл. 9.18. Сколько изделий каждого вида должно произвести предприятие, чтобы получить максимум прибыли, при условии, что число изделий A должно быть не менее 10, а B - не более 70 единиц?
Таблица 9.18
| Изделия | Затраты на изделие | Прибыль, | ||
| руб | ||||
| A B | ||||
| Фонд времени на операцию |
18.Предприятие должно выпустить по плану продукции A - 500 единиц, B - 300 единиц, C - 450 единиц на двух машинах, причем каждая может выполнить операции по производству всех трех видов продукции. Затраты времени на производстве единицы изделия каждой из двух машин приведены в табл. 9.19. Как распределить работу машин, чтобы затраты времени на выполнение плана были минимальны?
Таблица 9.19
| Машины | Продукция | ||
| A | B | C | |
19. Предприятию задана месячная программа по изготовлению четырех видов изделий в количествах: вида A - 5000, B - 2000, C - 3000, D - 1600. На предприятии имеется три группы станков с различной производительностью. Задается такое суммарное допустимое время работы за этот период для каждой группы станков: первой - 800 ч., второй - 1000 ч., третьей - 1500 ч. Нормы времени (в часах) на изготовление одного изделия на каждом станке и данные об издержках (в рублях) на изготовление каждого изделия на станках различных групп приводятся в табл. 9.20. Требуется так распределить изготовление изделий по группам станков, чтобы была обеспечена заданная программа по изготовлению изделий и чтобы общие издержки были минимальны.
Таблица 9.20
| Группы станков | Нормы времени на станках, час | Издержки на изготовление единицы изделия, руб | ||||||
| A | B | C | D | |||||
| 0,5 0,4 0,4 | 0,3 0,2 0,1 | 0,4 0,2 0,3 | 0,1 0,5 0,6 | 0,12 0,15 0,18 | 0,25 0,15 0,35 | 0,3 0,4 0,5 | 0,4 0,2 0,1 |
Глава 10.
Целочисленное И ДИНАМИЧЕСКОЕ программирование
Постановка задачи
Под задачей целочисленного программирования (ЦП) понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, когда хотя бы одна зависимость будет нелинейной, это будет целочисленной задачей нелинейного программирования.
Особый интерес к задачам ЦП вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных. В сфере лесного комплекса к их числу относятся следующие задачи:
· задачи оптимизации раскроя;
· оптимальное проектирование лесных машин и оборудования;
· оптимизации системы сервиса и технического обслуживания машинно-тракторного парка;
· и т.д.
Как уже отмечалось, часто задачу ЦП решают без учета условий целочисленности переменных, а затем округляют полученное решение с избытком или недостатком. Это не гарантирует получение оптимального целочисленного решения задачи. Поэтому для нахождения оптимального решения целочисленных задач применяют специальные методы, в которых учитывается, что число возможных решений любой целочисленной задачи является конечным. Следовательно, можно рассмотреть все возможные сочетания целочисленных переменных и проверить, удовлетворяют ли они ограничениям, и из числа удовлетворяющих ограничениям выбрать наилучшее с точки зрения целевой функции. Такой метод называют методом полного перебора. Его трудоемкость с ростом числа переменных и расширением области граничных условий значительно возрастает. Поэтому для реальных задач он неприменим.
На практике для решения реальных задач следует использовать методы, в которых все возможные альтернативы не рассматриваются. Наиболее распространенным является метод ветвей и границ.
Date: 2016-07-25; view: 4271; Нарушение авторских прав