
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задачи для решения в классе.
|
|
Задача. Найдите ОДР и максимум функции, если они существуют.

Задача 2. Найдите ОДР и минимум функции, если они существуют.

Задача 3. Найти ОДР и минимум функции, если они существуют..

Задача 4. Найдите ОДР и минимум функции, если они существуют.

Практика 3
Симплекс – метод
Симплекс – метод позволяет решать задачу при произвольном числе свободных переменных.
Пусть в задаче ЛП имеется n переменных и m независимых линейных ограничений, заданных в форме уравнений. Оптимальное решение будет достигаться в одной из опорных точек, где, по крайней мере, k из переменных обнуляются. Выберем некоторые k переменных в качестве свободный и выразим через них остальные m базисных переменных.
Более подробно этот метод рассмотрим на примере.
Пример.
Решить задачу симплекс-методом. л
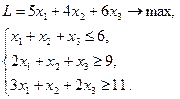
(8)
1. Переходим к основной задаче линейного программирования. Если в условиях ограничений даны неравенства, то добавлением соответствующих переменных необходимо привести ограничения к виду равенств. Если целевая функция стремится к минимальному значению, то сменой знака нужно сделать так, чтобы целевая функция стремилась к максимуму. Получим:
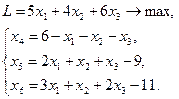 (9)
(9)
2. Правую часть уравнений (ограничения и целевую функцию) представляем в виде разности между свободным членом и суммой всех остальных.
 (10)
(10)
3. Составляем симплекс – таблицу: по горизонтали записываем свободные член и свободные переменные, по вертикали – целевую функцию и базисные переменные.
| bi | Х 1 | Х 2 | Х 3 | |||||
| L | -5 | -4 | -6 | |||||
| Х 4 | ||||||||
| Х 5 | -9 | -2 | -1 | -1 | ||||
| Х 6 | -11 | -3 | -1 | -2 | ||||
4. Проверяем, имеет ли задача допустимое решение:
а) если все свободные члены больше нуля, то допустимое решение существует;
б) если имеются уравнения с отрицательными свободными членами, то в этой строке должен быть хотя бы один отрицательный элемент, тогда допустимое решение существует, если же все элементы – положительные, то задача не имеет допустимого решения.
Задача имеет допустимое решение, так как имеются уравнения с отрицательными свободными членами и в этой строке есть отрицательные элементы.
5. Выбираем разрешающий элемент:
а) столбец, в котором находится отрицательный элемент, выбирается в качестве разрешающего (в тех строчках, где находятся отрицательные свободные члены);
б) в разрешающем столбце выбираются элементы, имеющие одинаковый знак со своим свободным членом; из них, в качестве разрешающего выбирается тот, для которого отношение к нему свободного члена будет минимальным.
| bi | Х 1 | Х 2 | Х 3 | ||||||
| L | -5 | -4 | -6 | ||||||
| Х 4 | 6/1=6 | ||||||||
| Х 5 | -9 | -2 | -1 | -1 | -9/(-2)=4,5 | ||||
| Х 6 | -11 | -3 | -1 | -2 | -11/(-3)=3,6 | ||||
6. Далее применяется алгоритм преобразования коэффициентов до нахождения опорного решения, т. е. когда все свободные члены станут больше нуля.
| bi | Х 1 | Х 2 | Х 3 | ||||||
| L | -5 | -4 | -6 | ||||||
| 55/3 | -5/3 | 5/3 | 10/3 | ||||||
| Х 4 | 6/1=6 | ||||||||
| -11/3 | 1/3 | -1/3 | -2/3 | ||||||
| Х 5 | -9 | -2 | -1 | -1 | -9/(-2)=4,5 | ||||
| 22/3 | -2/3 | 2/3 | 4/3 | ||||||
| Х 6 | -11 | -3 | -1 | -2 | -11/(-3)=3,6 | ||||
| 11/3 | -1/3 | 1/3 | 2/3 |
Меняем Х 1↔ Х 6
| bi | Х 6 | Х 2 | Х 3 | ||||||
| L | 55/3 | -5/3 | -7/3 | -8/3 | |||||
| 49/6 | 49/6 | 7/2 | 7/6 | ||||||
| Х 4 | 7/3 | 1/3 | 2/3 | 1/3 | 7/3:2/3=4,5 | ||||
| 7/2 | 1/2 | 3/2 | 1/2 | ||||||
| Х 5 | -5/3 | -2/3 | -1/3 | 1/3 | (-5/3): (-1/3)=5 | ||||
| 7/6 | 1/6 | 1/2 | 1/6 | ||||||
| Х 1 | 11/3 | -1/3 | 1/3 | 2/3 | 11/3: 1/3=11 | ||||
| -7/6 | -1/6 | -1/2 | -1/6 |
Меняем Х 2↔ Х 4
| bi | Х 6 | Х 4 | Х 3 | ||||||
| L | 53/2 | -1/2 | 7/2 | -3/2 | |||||
| 1/2 | -1 | -1/2 | -1/2 | ||||||
| Х 2 | 7/2 | 1/2 | 3/2 | 1/2 | 7/2:1/2=7 | ||||
| -1/2 | 1/2 | 1/2 | |||||||
| Х 5 | -1/2 | -1/2 | 1/2 | 1/2 | (-1/2): (-1/2)=1 | ||||
| -2 | -1 | -1 | |||||||
| Х 1 | 5/2 | -1/2 | -1/2 | 1/2 | |||||
| 1/2 | -1 | -1/2 | -1/2 |
Меняем Х 5↔ Х 6
| bi | Х 5 | Х 4 | Х 3 | ||||||
| L | -1 | -2 | |||||||
| Х 2 | |||||||||
| Х 6 | -2 | -1 | -1 | ||||||
| Х 1 | -1 | -1 | |||||||
7. Нашли допустимое решение. Находим оптимальное решение.
| bi | Х 5 | Х 4 | Х 3 | ||||||
| L | -1 | -2 | |||||||
| Х 2 | |||||||||
| Х 6 | -2 | -1 | -1 | ||||||
| Х 1 | -1 | -1 | |||||||
Меняем Х 2↔ Х 3
| bi | Х 5 | Х 4 | Х 3 | ||||||
| L | |||||||||
| Х 2 | |||||||||
| Х 6 | -1 | -1 | |||||||
| Х 1 | -1 | -1 | |||||||
Оптимальное решение найдено.
Дополнительные задачи для закрепления материала.
Задачи для решения.
Решить задачу симплекс – методом.

Задача 3. Решить задачу симплекс – методом.

Задача 4. Решить задачу симплекс – методом.
Практика 4
Двойственная задача
В каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу Л.П, которая называется двойственной или сопряженной по отношению к исходной или прямой.
Пусть имеется прямая задача, заключающаяся в определении max функции F=a1x1+ a2x2+…+anxn→max,
При условии:
a11x1+ a12x2+…+a1nxn <b1,
…………………………..
ak1x1+ ak2x2+…+aknxn <bk,
………………………….
am1x1+ am2x2+…+amnxn <bm, при этом хj >0 (j=1,l,l<n)
Двойственными называются задачи, состоящие в определении min функции
G=b1y1+ b2y2+…+bnyn → min, при условиях:
a11y1+ a21y2+…+am1ym >c1,
…………………………..
a1ly1+ a2ly2+…+amlym >cl,
a1ny1+ a2ny2+…+amnym >cn, при этом yi >0 (i=1,k,k<m).
Двойственная задача по отношению к прямой задачи составляется согласно следующим правилам.
1. Если прямая задача - задача max, то двойственная задача min.
2. Коэффициенты целевой функции прямой задачи c1,с2,…,сn становятся свободными членами ограничений двойственной задачи.
3. Свободные члены ограничений прямой задачи b1,b2,…,bm становятся коэффициентами целевой функции двойственной задачи.
4. Матрица ограничений двойственной задачи получается путем транспонирования матрицы ограничений прямой задачи.
5. Число переменных в двойственной задачи равно числу ограничений прямой задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи.
6. Если переменная xj прямой задачи может принимать только неотрицательные значения, j-ое ограничение в двойственной задачи является неравенством вида >. Если же переменная xj может принимать как положительные, так и отрицательные значения, то j-ое ограничение в двойственной задачи - это уравнение.
Запишем в матричном виде правило перехода от прямой задачи к двойственной.
| Прямая задача: | Двойственная задача: |
Найти max f( )=max )=max  при
при  (3.11)
(3.11)
| Найти min L( )= )=  при
при 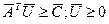 (3.12)
(3.12)
|
Date: 2016-07-25; view: 389; Нарушение авторских прав