Центрированная оптическая система

Случай преломления на одной сферической поверхности сравнительно редок. Большинство реальных преломляющих систем содержит по крайней мере две преломляющие поверхности (линза) или большее их число.

Система сферических поверхностей называется центрированной, если центры всех поверхностей лежат на одной прямой, которая называется главной оптической осью системы.

Рис.1. Центрированная оптическая система.

(1)

(1) – условие синусов Аббе или условие Лагранжа-Гемгольца.

Из него вытекает, что преобразование данного оптического пучка при помощи оптической системы в другой пучок любого наперед заданного строения невозможно. Строение преобразованного пучка может быть только таким, какое допускает условие Лагранжа-Гемгольца.

Гомоцентрический параксиальный пучок остается гомоцентрическим при произвольном числе преломлений (отражений) в центрированной сферической системе, то есть точка дает в центрированной системе стигматическое изображение (действительное или мнимое).

Для центрированной системы сохраняется смысл и понятие главных плоскостей таких как сопряженных плоскостей, в которых объект и изображение имеют одинаковые величину и направление.

ПРЕЛОМЛЕНИЕ В ЛИНЗЕ. ОБЩАЯ ФОРМУЛА ЛИНЗЫ.

Центрированная система, состоящая из двух сферических поверхностей, ограничивающих какой-либо прозрачный хорошо преломляющий материал (обычно стекло) от окружающего воздух-линза. Линза называется тонкой, если .

– оптический центр линзы.

Луч, проходящий через оптический центр, называется осью линзы. Та из осей, которая проходит через центры обеих поверхностей, называется главной осью, остальные – побочными.

Рис.2. Преломление в тонкой линзе (ТЛ)

Для первой преломляющей поверхности: (2) Преломление на создало бы без второй в сплошной среде с изображение на расстоянии , формула (2)

Для первой преломляющей поверхности: (3) Для является как бы мнимым источником света. После преломления на даст точку , , формула (3)

Так как , то имеем

,

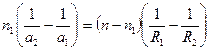
или

, (4)

где ; , , 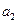, 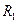– положительно, если отложены вправо от линзы и отрицательно, если отложены влево от линзы. Если знаки и 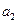– одинаковы, то одна из точек сопряженных – мнимая, то есть в ней пересекаются не сами лучи, а их воображаемые продолжения.

ФОКУСНЫЕ РАССТОЯНИЯ ТОНКОЙ ЛИНЗЫ.

Положение изображения, соответствующее предельному случаю, когда источник удален в бесконечность, носит название фокуса линзы. Таким образом, фокус есть точка, сопряженная бесконечно удаленной точке главной оси, расстояние от линзы до фокуса есть фокусное расстояние тонкой линзы. Плоскость, проходящая через фокус перпендикулярно к главной оси, называется фокальной плоскостью.

Рис.3. Положение фокусов, расположенных на главной и побочной оптических осях. – фокальная плоскость.

при (5)

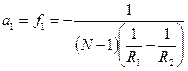при (6)

То есть – фокусные расстояния линзы равны по величине и противоположны по знаку. То есть фокусы лежат по разные стороны от линзы. В зависимости от знака и величины 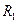и , а также от знака , величина 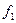может быть положительной или отрицательной, то есть фокус может быть мнимым или действительным.

Если , то линза называется собирательной или положительной.

Если , то линза называется рассеивающей или отрицательной.

Рис.4. Линзы: () – собирательные, () – рассеивающие.

Если материал тонкой линзы преломляет меньше, чем окружающая среда (например, воздушная полость в воде), то линзы вида () будут рассеивающими, а вида () – собирательными.

ИЗОБРАЖЕНИЕ В ТОНКОЙ ЛИНЗЕ. УВЕЛИЧЕНИЕ.

(7)

– изображение действительное и перевернутое;

– изображение мнимое, прямое.

Рис.5.

Оптическая сила линзы называется величина обратная заднему фокусному расстоянию и ее выражают в диоптриях:

. (8)

Гаусс (1841г.) дал общую теорию оптических систем. Его теория – теория идеальной оптической системы, в которой сохраняется гомоцентричность пучков и изображение геометрически подобно предмету. Всякой точке пространства объектов соответствует в идеальной системе точка пространства изображений. Эти точки носят название сопряженных. Точно также каждой прямой или плоскости пространства объектов должна соответствовать сопряженная прямая или плоскость пространства изображений. Теория Гаусса устанавливает ряд так называемых кардинальных точек и плоскостей, задание которых полностью описывает все свойства оптической системы и позволяет пользоваться ею, не рассматривая реального хода лучей в системе.

Рис.6. Схема центрированной системы с главными плоскостями системы.

Рассмотрим центрированную систему (Рис.6.). – главная оптическая ось системы, луч 1 и 2 параксиальные 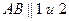. По теории Гаусса мысленно продолжаем луч 1 внутри системы (Рис.6.) пунктиром, а справа он выходит из некоторой точки и пересекает ось в точке 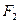называемой правым фокусом системы. Как луч проходит внутри системы нас не интересует. Луч 2, идущий параксиально справа налево и выходит из некоторой точки и пересекает оптическую ось в точке 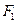(левый фокус). Лучи 1 и 2, построенные указанным способом, называются сопряженными. Теперь продолжим лучи 1 и 2, вышедшие из системы, до пересечения с пунктирной линией, показывающей их первоначальное направление. Через полученные точки и проведем плоскости, перпендикулярные оси ( и ). Эти плоскости I и II называются главными плоскостями системы. Параллельные им плоскости, проходящие через 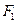и 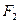называются фокальными плоскостями. Точки пересечения главной оптической оси с главными плоскостями будем называть главными точками (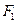, , 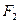, ). Расстояния от главных точек до фокусов представляют фокальные (или фокусные) расстояния (левое и правое, или переднее и заднее). В тонкой линзе главные плоскости I и II сливаются в одну – в этом и состоит ее отличие (основное) от любой другой центрированной оптической системы (Рис.7).

Рис.7. Схематическое изображение центрированной

системы при условии параксиальности.

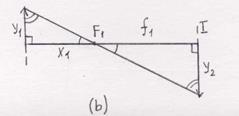
Рассмотрим Рис.8, слева от системы находится объект (стрелка). Найдем расположение и величину изображения этого предмета. Для этого сделаем построения, показанные на Рис.8. Где – расстояние от первого фокуса 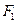до объекта и – расстояние от второго фокуса 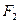до изображения. Из образовавшихся треугольников (подобные по трем углам) находим:

() , ()

() , ()

Следовательно или

– формула Ньютона (9)

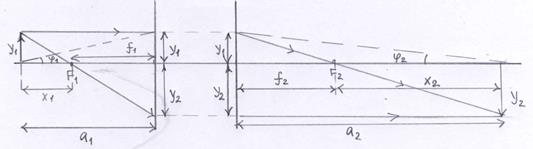
Рис.8. К выводу формулы Ньютона.

Применив ее к сферической поверхности раздела двух сред с показателями преломления 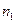и , то есть объединим с формулой Лагранжа-Гемгольца, получим

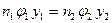(10)

Из Рис.8 видно, что

, (11)

Из формулы (10) следует

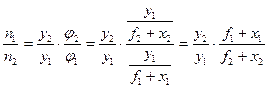
Из формулы (8) имеем

Следовательно

Из формулы (9) следует , то есть

(12)

Если вновь ввести правило знаков, то расстояние 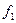нужно считать отрицательным и формулу (12) записывать:

, (13)

так как .

В качестве примера рассмотрим оптическую систему – лупу, то есть двояковыпуклую линзу, используемую для увеличения мелких предметов (Рис.9).

Рис.9. Ход лучей в лупе.

Согласно формуле (11) с учетом , следовательно . Поместив объект между фокусом и лупой, получим увеличенное мнимое изображение объекта . Назовем отношение к «увеличением лупы» .

(14)

Из формулы линзы: находим

(15)

(16)

Введем расстояние наилучшего зрения . Для нормального глаза оно равно 25 см от объекта до глаза. Следовательно, глаз должен находится на расстоянии от лупы, определяемом соотношением

. (17)

Знак «-» показывает, что эта величина отложена влево от лупы. Из формулы (16) и соотношения (17) получаем

(18)

Тогда, если глаз расположен в фокальной плоскости, то и

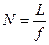. (19)

Так как величина обратная фокусному расстоянию линзы есть оптическая сила линзы, то формулу (19) запишем в виде:

, (20)

где .

Выражение (20) также называется поперечным увеличением объекта. Так как , то обычно применяемые лупы дают увеличение от 2,5 до 25 раз. Для близорукого глаза меньше и, следовательно, лупа оказывает меньшую помощь в распознавании деталей.

Для получения больших увеличений применяют комбинацию двух оптических систем (двух линз). Представим эти системы в соответствии с теорией Гаусса (Рис.10).

Рис.10. Нахождение фокуса и главной плоскости сложной оптической системы.

– расстояние между главными плоскостями, 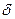– расстояние между фокальными плоскостями, – общая главная плоскость системы, находящаяся вне и , – фокус всей системы, – расстояние от до .

Из Рис.10 следует

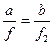, (21)

, следовательно .

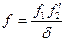Если , то

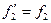, (22)

или 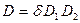(23)

(24)

Следовательно

(25)

Если , то есть фокальные плоскости линз и расположены так, что фокус 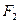находится левее фокуса 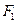, то формула (25) будет иметь вид

(26)

Для соприкасающихся линз получаем

, (27)

то есть оптическая сила соприкасающихся линз равна сумме их оптических сил.

Применив соображении, рассматриваемые выше, к линзе легко теперь записать в явном виде фокусное расстояние для толстой линзы:

,

где – толщина линзы.

ОПТИЧЕСКИЕ ИНСТРУМЕНТЫ,

Date: 2016-07-25; view: 896; Нарушение авторских прав