
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема лекции 1 Введение. Дифференциальное уравнение изогнутой линии балки. Перемещения при изгибе.
|
|
Конспект лекции
1.1 Основные понятия прочности и надежности машин.
1.1.1 Задачи курсапрочности и надежности машин. Различные сооружения и машины, проектированием и строительством которых занимается инженер в своей практической деятельности, помимо других качеств должны обязательно обладать прочностью, т. е. способностью сопротивляться разрушению под действием приложенных к ним внешних сил (нагрузок).
Изложение методов расчета элементов конструкций на прочность и составляет первую задачу курса сопротивления материалов.
Во многих случаях приходится определять те изменения формы и размеров (деформации), которые возникают в элементах конструкций при действии нагрузок.
Способность элемента конструкции сопротивляться деформации называется жесткостью.
Отсюда вторая задача курса: изложение методов расчета элементов конструкций на жесткость.
Третья задача сопротивления материалов связана с изучением устойчивости форм равновесия реальных (т. е. деформирующихся) тел.
Под устойчивостью понимают способность элемента сопротивляться возникновению больших отклонений от невозмущенного равновесия при малых возмущающих воздействиях.
Признаком потери устойчивости является внезапная смена одной формы равновесия другой.
При выполнении указанных видов расчета необходимо стремиться к максимальной экономии материалов, т. е. к достаточным, но не завышенным размерам деталей машин и сооружений.
1.1.2 Внутренние силы. Метод сечений. Внутренние силы (силы упругости), возникающие в теле под действием нагрузки, - силы непрерывно распределенные (в соответствии с принятым допущением о непрерывности материала тела).
Для определения внутренних усилий (или внутренних силовых факторов) применяется метод сечений, заключающийся в следующем.
Для тела, находящегося в равновесии (рис.1.1), в интересующем нас месте мысленно делается разрез, например по а – а затем одна из частей отбрасывается (обычно та, к которой приложено больше сил). Взаимодействие частей друг на друга заменяется внутренними усилиями, которые уравновешивают внешние силы, действующие на отсеченную часть.
В общем случае могут возникать шесть внутренних усилий, являющихся компонентами главного вектора и главного момента системы внутренних сил (рис. 1.1); продольная сила, N, поперечная сила Qх, поперечная сила Qу и три момента: Мх, Му и М  , причем первые два являются изгибающими, а третий М
, причем первые два являются изгибающими, а третий М  ,действующий в плоскости сечения, называется крутящим Мкр, так как он возникает при закручивании стержня. Для определения этих шести усилий необходимо использовать шесть уравнений равновесия: приравнять нулю суммы проекций сил (приложенных к отсеченной части) на три оси координат и приравнять нулю суммы моментов сил относительно трех осей, имеющих начало в центре тяжести сечения.
,действующий в плоскости сечения, называется крутящим Мкр, так как он возникает при закручивании стержня. Для определения этих шести усилий необходимо использовать шесть уравнений равновесия: приравнять нулю суммы проекций сил (приложенных к отсеченной части) на три оси координат и приравнять нулю суммы моментов сил относительно трех осей, имеющих начало в центре тяжести сечения.
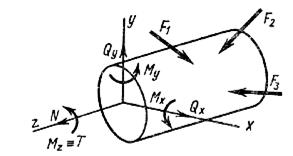 |
Рисунок 1.1
Итак, для нахождения внутренних усилий необходимо: 1) разрезать стержень или систему стержней; 2) отбросить одну часть; 3) приложить в сечении усилия, способные уравновесить внешние силы, действующие на отсеченную часть; 4) найти значения усилий из уравнений равновесия, составленных для отсеченной части.
1.2 Растяжение–сжатие. Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием).
1.2.1 Продольные силы и их эпюры. Растягивающие продольные силы принято считать положительными, а сжимающие — отрицательными.
На рис.1.4, a изображен брус, нагруженный силами P1 и Р2 направленными вдоль его оси, двумя силами Р3; параллельными оси и приложенными на равных расстояниях от нее в поперечном сечении с, а также двумя силами Р4., направленными под углом 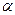 к оси бруса и приложенными в поперечном сечении d на равных расстояниях от оси.
к оси бруса и приложенными в поперечном сечении d на равных расстояниях от оси.
На рис.1.4,б изображена расчетная схема, полученная путем замены бруса его осью и переноса внешних нагрузок к этой оси.
Силы Р1 и Р2 расчетной схеме действуют вдоль оси бруса; силы Р3 силы Р4 (рис.1.2, а) приводятся соответственно к силам 2Р3 и 2Р4cos 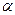 , также направленным вдоль оси. Таким образом, на расчетной схеме (рис.1.2,б) все внешние силы действуют вдоль оси бруса. Следовательно, в поперечных сечениях рассматриваемого бруса возникают только продольные силы.
, также направленным вдоль оси. Таким образом, на расчетной схеме (рис.1.2,б) все внешние силы действуют вдоль оси бруса. Следовательно, в поперечных сечениях рассматриваемого бруса возникают только продольные силы.
 |
Рисунок 1.2
Определим в качестве примера продольную силу n1 в сечении I—I (рис. 1.2,б). На рис.1.2, в, г показаны продольные силы n1, действующие на левую (относительно сечения I—I) и на правую части бруса. Направления этих сил приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение n1 получается со знаком минус, то это означает, что в действительности брус в сечении I—I сжат.
Для определения силы n  воспользуемся методом сечений. Составим уравнение равновесия в виде суммы проекций на ось бруса всех сил, действующих на левую его часть (рис.1.2, в):
воспользуемся методом сечений. Составим уравнение равновесия в виде суммы проекций на ось бруса всех сил, действующих на левую его часть (рис.1.2, в):
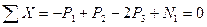
откуда

Силы P1 и 2Р3 взяты со знаком плюс, потому что их направление совпадает с положительным направлением силы n1, действующей на правую часть бруса.
Аналогично найдем продольные силы в сечениях II—II, III—III, IV—IV (рис. 1.2,б), проецируя силы, приложенные слева от этих сечений, на ось бруса:
N11=Р1; N111=P1- 
 .
.
Очевидно, что на всем участке аЬ (между точками приложения сил Р1 и Р2) продольная сила постоянна и равна P1; аналогично и на других участках (между точками приложения внешних сил) продольные силы имеют постоянные значения.
Построим график, показывающий изменение продольных сил по длине оси бруса, называемый эпюрой продольных сил (эпюрой N). Для этого проведем ось эпюры ае, параллельную оси бруса (рис 1.2, д), и перпендикулярно ей отложим ординаты, изображающие в некотором масштабе значения продольных сил в поперечных сечениях бруса. Полученную таким путем эпюру принято штриховать (так же как и эпюры других внутренних усилий, рассматриваемые в последующих главах курса) прямыми линиями, перпендикулярными ее оси. Каждая такая линия в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении бруса.
В поперечном сечении, в котором к брусу приложена сосредоточенная сила, не перпендикулярная его оси, значение продольной силы изменяется скачкообразно: слева от этого сечения продольная сила имеет одно, а справа – другое значение, отличающееся на величину проекции (на ось бруса) указанной сосредоточенной силы. В соответствии с этим эпюра, изображенная на рис. 1.2,д, имеет скачки (уступы) в точках а, Ь, с, d, e, равные соответственно величинам 
 и значению реакции опорного закрепления бруса.
и значению реакции опорного закрепления бруса.
1.2.2 Напряжения и деформации при растяжении-сжатии. Продольная сила N, возникающая в поперечном сечении бруса, представляет собой равнодействующую внутренних нормальных сил, распределенных по площади поперечного сечения, и связана с возникающими в этом сечении нормальными напряжениями зависимостью:
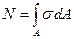 , (1.2.1)
, (1.2.1)
здесь  —нормальное напряжение в произвольной точке поперечного сечения, принадлежащей элементарной площадке dA, причем во всех точках поперечного сечения
—нормальное напряжение в произвольной точке поперечного сечения, принадлежащей элементарной площадке dA, причем во всех точках поперечного сечения  = const; A—площадь поперечного сечения бруса.
= const; A—площадь поперечного сечения бруса.
Произведение  d.A== dN представляет собой элементарную внутреннюю силу, приходящуюся на площадку dA. Таким образом,
d.A== dN представляет собой элементарную внутреннюю силу, приходящуюся на площадку dA. Таким образом,
 (1.2.2)
(1.2.2)
откуда
 (1.2.3)
(1.2.3)
Итак, в поперечных сечениях бруса при центральном растяжении или сжатии возникают равномерно распределенные нормальные напряжения, равные отношению продольной силы к площади поперечного сечения.
Рассмотрим теперь напряжения в наклонных сечениях бруса.
Обозначим 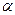 угол между наклонным сечением п—п1 и поперечным сечением п—п2 (рис. 1.3, а). Угол
угол между наклонным сечением п—п1 и поперечным сечением п—п2 (рис. 1.3, а). Угол 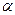 условимся считать положительным, когда поперечное сечение для совмещения с наклонным сечением надо повернуть на этот угол против часовой стрелки.
условимся считать положительным, когда поперечное сечение для совмещения с наклонным сечением надо повернуть на этот угол против часовой стрелки.
Рассмотрим нижнюю часть бруса, отсеченную сечением п—п1 (рис. 1.3,б). Из условий ее равновесия следует, что полные напряжения р параллельны оси бруса и направлены в сторону, противоположную силе Р.
Значения  и
и  , получим из выражений
, получим из выражений
 = р cos
= р cos 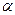 =
=  cos2
cos2 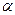 ; (1.2.4)
; (1.2.4)
 =р sin
=р sin 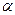 =
=  sin
sin 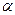 cos
cos 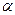 = (
= ( /2) sin 2
/2) sin 2 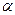 . (1.2.5)
. (1.2.5)
Нормальное напряжение считается обычно положительным при растяжении и отрицательным при сжатии. Касательное напряжение положительно, если изображающий его вектор стремится вращать тело относительно любой точки С, лежащей на внутренней нормали к сечению, по часовой стрелке. На рис. 1.3, в напряжения  и
и  положительные.
положительные.
Рассмотрим прямой брус постоянного сечения длиной l, заделанный одним концом и нагруженный на другом конце растягивающей силой Р (рис. 1.4, а). Под действием силы Р брус удлиняется на неко- торую величину  , которая называется полным (или абсолютным) удлинением (абсолютной продольной деформацией). В любых точках рассматриваемого бруса имеется одинаковое напряженное состояние и, следовательно, линейные деформации
, которая называется полным (или абсолютным) удлинением (абсолютной продольной деформацией). В любых точках рассматриваемого бруса имеется одинаковое напряженное состояние и, следовательно, линейные деформации  для всех его точек одинаковы. Поэтому значение
для всех его точек одинаковы. Поэтому значение 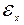 можно определить как отношение абсолютного удлинения
можно определить как отношение абсолютного удлинения  к первоначальной длине бруса l, т.е.
к первоначальной длине бруса l, т.е.  / l.
/ l.

Рисунок 1.3
 Линейную деформацию
Линейную деформацию  при растяжении или сжатии брусьев называют обычно относительным удлинением (или относительной продольной деформацией) и обозначают
при растяжении или сжатии брусьев называют обычно относительным удлинением (или относительной продольной деформацией) и обозначают 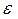 .
.
Следовательно,
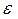 =
= 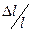 (1.2.6)
(1.2.6)
Относительная продольная деформация выражается в отвлеченных единицах. Деформацию удлинения условимся считать положительной (рис.1.4, а), а деформацию сжатия—отрицательной (рис. 1.4, б).
Чем больше сила, растягивающая брус, тем больше при прочих равных условиях удлинение бруса; чем больше площадь поперечного сечения бруса, тем удлинение бруса меньше. Брусья из различных материалов
Рисунок 1.4 удлиняются различно. Для случаев, когда напряжения в брусе не превышают предела пропорциональности, опытом установлена следующая зависимость:
 . (1.2.7)
. (1.2.7)
Здесь N—продольная сила в поперечных сечениях бруса; A—площадь поперечного сечения бруса; Е— коэффициент, зависящий от физических свойств материала.
Учитывая, что нормальное напряжение в поперечном сечении бруса  =N/А, получаем
=N/А, получаем
 , ( 1.2.8)
, ( 1.2.8)
откуда
 . (1.2.9)
. (1.2.9)
Абсолютное удлинение бруса выражается формулой
 , (1.2.10)
, (1.2.10)
т. е. абсолютная продольная деформация прямо пропорциональна продольной силе (при постоянных N и EA).
Впервые закон о прямой пропорциональности между силами и деформациями сформулировал Р. Гук (в 1660г.). Формулы (1.2.7)...(1.2.10) являются математическими выражениями закона Гука при растяжении и сжатии бруса. Более общей является следующая формулировка закона Гука: относительная продольная деформация прямо пропорциональна нормальному напряжению.
 |
Рисунок 1.5
В такой формулировке закон Гука используется не только при изучении растяжения и сжатия брусьев, но и в других разделах курса.
Величина Е называется модулем упругости первого рода (сокращенно—модулем упругости). Это физическая постоянная материала, характеризующая его жесткость. Чем больше значение Е, тем меньше при прочих равных условиях продольная деформация. Из формулы (10) видно, что модуль упругости выражается в тех же единицах, что и напряжение, т. е. в Паскалях (Па).
Произведение EА называется жесткостью поперечного сечения бруса при растяжении и сжатии. В приложении I приведены значения модулей упругости Е для различных материалов.
Формулой (12) можно пользоваться для вычисления абсолютной продольной деформации участка бруса длиной l лишь при условии, что сечение бруса в пределах этого участка постоянно и продольная сила N во всех поперечных сечениях одинакова.
Кроме продольной деформации при действии на брус сжимающей или растягивающей силы наблюдается также поперечная деформация. При сжатии бруса поперечные размеры его увеличиваются, а при растяжении—уменьшаются. Если поперечный размер бруса до приложения к нему сжимающих сил Р обозначить b, а после приложения этих сил b+  b (рис. 1.5), то величина
b (рис. 1.5), то величина  b будет обозначать абсолютную поперечную деформацию бруса. Отношение
b будет обозначать абсолютную поперечную деформацию бруса. Отношение  является относительной поперечной деформацией.
является относительной поперечной деформацией.
Опыт показывает, что при напряжениях, не превышающих предела упругости, относительная поперечная деформация  прямо пропорциональна относительной продольной деформации
прямо пропорциональна относительной продольной деформации  , но имеет обратный знак:
, но имеет обратный знак:

 (1.2.11)
(1.2.11)
Коэффициент пропорциональности  в формуле (1.2.11) зависит от материала бруса. Он называется коэффициентом поперечной деформации (или коэффициентом Пуассона) и представляет собой отношение относительной поперечной деформации к продольной, взятое по абсолютной величине, т. е.
в формуле (1.2.11) зависит от материала бруса. Он называется коэффициентом поперечной деформации (или коэффициентом Пуассона) и представляет собой отношение относительной поперечной деформации к продольной, взятое по абсолютной величине, т. е.
 . (1.2.12)
. (1.2.12)
Коэффициент Пуассона наряду с модулем упругости Е характеризует упругие свойства материала.
Коэффициент Пуассона определяется экспериментально. Для различных материалов он имеет значения от нуля (для пробки) до величины, близкой к 0,50 (для резины и парафина). Для стали коэффициент Пуассона равен 0,25...0,30; для ряда других металлов (чугуна, цинка, бронзы, меди) он имеет значения от 0,23 до 0,36.
Основная литература 2[гл.1, §1,стр.4-15, §5,стр.15-22],3[гл.2, §2.1,стр.22-32],1[гл.1, §10,стр.42-44]
Дополнительная литература 7,9
Контрольные вопросы:
- Основные задачи курса сопротивления материалов.
- Какие силы называются внутренними, и перечислите их.
- Как вычисляются напряжения в поперечных и наклонных сечениях бруса.
- Как формулируется закон Гука при растяжении-сжатии?
- Какие упругие постоянные материалов вы знаете?
- Как вычисляется потенциальная энергия деформации при растяжении-сжатии?
| <== предыдущая | | | следующая ==> |
| Вычисления в таблице | | | Основы экономической психологии |
Date: 2016-07-25; view: 315; Нарушение авторских прав