Решение задачи с помощью электронных таблиц.

Компьютерная модель задачи:

1) Для начала перенесём все данные в электронную таблицу.

Рисунок 1. Исходные данные.

2) Создадим схожую таблицу и в ячейках B-12 до G-16 – область значений переменных, в которую предварительно запишем нули.

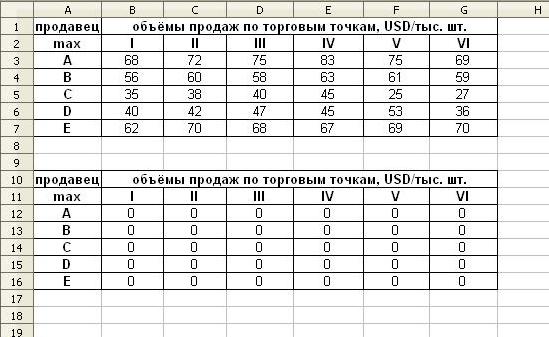
Рисунок 2. Таблица с нулевыми коэффициентами.

3) В созданной таблице (во втором пункте) под каждой должностью найдём сумму всех коэффициентов каждого работника и у каждого работника найдём сумму коэффициентов каждой должности. В целевой ячейке найдем сумму произведения эффективностей работы (См. приложение 1).

Рисунок 3. Вставка формул в таблицу.

4) Откроем решатель и выставим все ограничения. Результат поставим максимум. В конце каждого столбца торговых точек ограничение будет <= 1, в конце каждой строки продавцов ограничения будут = 1. Изменять будем все коэффициенты эффективности в этой таблице.

Рисунок 4. Ограничения. Ячейки B17-E17

Рисунок 5. Ограничения. Ячейки F17-G17, H12-H13

Рисунок 6. Ограничения. Ячейки H14-H16

5) В параметрах поставим ограничение глубины ветвей и границ, переменные как неотрицательные и как целочисленные.

Рисунок 7. Параметры решателя.

6) Нажимаем «ОК» и нажимаем «Решить». Получим следующие результаты:

Рисунок 8. Итог компьютерной модели.

Исходя из получившегося ответа, следует, что решённая мной задача методом «ветвей и границ» решена правильно.

Глава 3. Аналитическая часть.

Приведённая задача была решена мною двумя способами («метод ветвей и границ» и с помощью функции «Решатель» в программе OpenOffice Calc). В обоих случаях мои ответы совпали, значит, данная задача решена, верно.

Следовательно, максимальная эффективность 306 USD/тыс. шт. будет достигнута при следующих назначениях:

Продавец А пойдёт на IV должность;

Продавец B пойдёт на II должность;

Продавец C пойдёт на III должность;

Продавец D пойдёт на V должность;

Продавец E пойдёт на VI должность;

I должность является неэффективной.

При решении задачи методом ветвей и границ мне необходимо было добавить к условию задачи мнимого продавца с нулевой эффективностью работы. Без этого задача была бы решена неверно, и ответ был бы абсолютно другим. Так же было необходимо внимательно и точно выполнять каждый шаг из алгоритма, чтоб не допускать ошибок и найти при каких назначениях эффективность будет максимальна.

При решении задачи в OpenOffice Calc времени было затрачено не много. Необходимо было ввести лишь ограничения, целевую ячейку, область изменяемых ячеек и в параметрах решателя выставить необходимые по условию параметры. Но мы зато не можем узнать почему (по какому алгоритму) и как был достигнут именно этот результат.

Исходя из этого, можно сделать вывод. Если у нас нет времени на решение подобных задач, то вполне можно воспользоваться «Решателем» из OpenOffice Calc. Если же нам необходимо точно знать по какому принципу (алгоритму) были выбраны именно эти назначения и у нас имеется достаточно времени для решения этих задач тогда можно воспользоваться «методом ветвей и границ».

ЗАКЛЮЧЕНИЕ

Цель моей курсовой работы достигнута. Я разобралась в сути самого метода, научилась решать задачи методом ветвей и границ, и успешно применила его на практике.

Практика порождает все новые и новые задачи оптимизации, причем их сложность растет. Требуются новые математические модели и методы, которые учитывают наличие многих критериев, проводят глобальный поиск оптимума. Другими словами, жизнь заставляет развивать математический аппарат оптимизации.

Реальные прикладные задачи дискретной оптимизации очень сложны. Современные методы оптимизации далеко не всегда справляются с решением реальных задач без помощи человека. Нет, пока такой теории, которая учла бы любые особенности функций, описывающих постановку задачи. Следует отдавать предпочтение таким методам, которыми проще управлять в процессе решения задачи.

СПИСОК ЛИТЕРАТУРЫ

1. Корбут А.А., Финкельштейн Ю.Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.

2. Береснев В.Л., Гимади Э.Х., Дементьев В.Т. Экстремальные задачи стандартизации. Новосибирск. Наука, 1978.

3. Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы. М.: ФИЗМАТЛИТ, 2003. -- 240 с.

4. http://www.coolreferat.com

5. Лекции по дисциплине: «Математические методы и математической статистике» за I семестр III курса.

ПРИЛОЖЕНИЕ

Date: 2016-07-25; view: 510; Нарушение авторских прав