Приклад 2.Дослідити на збіжність ряди: а) б) .

Розв’язання а)Ряд 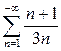розбігається оскільки

б) . Розглянемо часткову суму

.

Отже, ряд б) збігається та його сума дорівнює .

Зауважимо, що знайти точне значення суми ряда вдається рідко.

Дослідження рядів звичайно провадиться в два етапи;

1.З’ясовується, чи збігається ряд.

2.Обчислюється точно або наближено його сума.

На відміну від обчислення суми ряда задача про з’ясування його збіжності є набагато ростішою та розв’язується за допомогою теорем порівняння та ознак збіжності.

Якщо ряди збігаються, то їх можна множити на числа або додавати.

Теорема 2. Якщо ряди збігаються, то збігається ряд 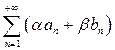та його сума

Зокрема,

Теореми порівняння

Теореми порівняння дозволяють для рядів з додатними членами зробити висновок про поведінку ряду без обчислення частковоі суми .

Для застосування теорем порівняння потрібні еталонні ряди, з якими проводиться порівняння. Такими рядами є геометричний ряд, розглянутий в п.1 та гармонічний ряд

(1)

Теорема 3.Перша теорема порівняння. Нехай є два додатніх ряди 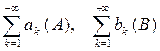(2)

Якщо , то із збіжності ряду (B) випливає збіжність ряду (A),а із розбіжності ряду (A) випливає розбіжність ряду (B).

Приклад1. Дослідити на збіжність ряд (А-1) 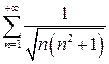. Розв’язання. =

. Ряд (А-1) збігається за теоремою 3, оскільки ряд збігається

як гармонічний .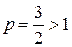

Теорема 4.Друга, гранична теорема порівняння. 1.Якщо

, (3)

де С –стала, то при ряд (A) збігається,а при розбігається.

2.Якщо (4)

то ряд (A) збігається.

Приклад 2. Дослідити на збіжність ряди: а):(А-2) .б) (А-3) .

Розв’язання. а) .Тут . За теоремою 4 ряд (А-2) розбігається.

б) . Оскільки геометричний ряд збігається,, , то ряд (А-3) збігається.

3.Ознака збіжності Д’Аламбера.

Теорема 5. Якщо для додатного ряду існує границя , то ряд збігається при і розбігається 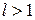при . При ряд може як збігатися,так і розбігатися.

Приклад 3.Дослідити на збіжність ряд (А-4) . Розв’язання ряд збігається за ознакою Д’Аламбера.

Знакозмінні ряди

Означеня 1. Знакозмінним називається ряд, злени якого по черзі мають то додатній то від’ємний знак:

(1)

Означеня 2. Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд складений з модулей его членів ряд

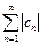(2)

Приклад1. Ряд збігається абсолютно, оскільки ряд збігається р =2>1.

Теорема 1. Ознака абсолютної збіжності. Нехай дан ряд (1).Якщо збігається ряд, який складається з модулей члені ряда (1), то ряд (1) також збігається.

Означеня 3. Ряд (1) може збігатися, хоч ряд з модулей ро збігається. Такі ряди називаються умовно збіжними.

Date: 2016-07-25; view: 402; Нарушение авторских прав