
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Экономико-математическое моделирование в экономическом анализе
|
|
Математическое моделирование экономических явлений и процессов дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Содержание метода моделирования составляют конструирование модели на основе предварительного изучения объекта и выделения его существенных характеристик, экспериментальный или теоретический анализ модели, сопоставление результатов с данными об объекте, корректировка модели. На практике постоянно встречаются такие ситуации, когда достичь какого-то результата можно не одним, а многими различными способами. Естественно, что когда решений много, ищется в каком-то случае наилучшее. Математически это сводится к нахождению наибольшего или наименьшего значения некоторой функции:
f(x) ® max (min) хÎ Х
5.2.1. Методы линейного программирования
Методы линейного программирования оформились как отдельный раздел прикладной математики в 40-х – 50-х годах ХХ века, когда выяснилось, что целый ряд задач из сферы планирования и управления может быть сформулирован в виде задач линейного программирования. Эксперты считают, что в настоящее время примерно 80-85% всех решаемых на практике задач оптимизации относятся к задачам линейного программирования. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.
С помощью этого метода в промышленном производстве, например, исчисляется оптимальная общая производительность машин, агрегатов, поточных линий (при заданном ассортименте продукции и иных заданных величинах), решается задача рационального раскроя материалов (с оптимальным выходом заготовок). В сельском хозяйстве он используется для определения минимальной стоимости кормовых рационов при заданном количестве кормов (по видам и содержащимся в них питательным веществам). Задача о смесях может найти применение и в литейном производстве (состав металлургической шихты). Этим же методом решаются транспортная задача, задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.
Все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. Для решения таких задач разработаны эффективные методы, один из которых (симплекс-метод) мы рассмотрим при решении примера 6.1
Таблица 4.1.
Экономико-математические методы и сфера их применения в экономическом анализе
| Метод | Сущность метода | Сфера применения в экономическом анализе |
| 1. Выборочный метод | На основе изучения выборочной совокупности, выделенной из генеральной совокупности объектов, делаются заключения о всей генеральной совокупности. Необходимость применения выборочного метода связана с невозможностью обследования каждого объекта совокупности ввиду их многочисленности. Чтобы выборка давала правильное представление о массовом явлении, вероятность должна быть выбрана одинаковой для всех объектов, соблюдена достаточная выборка, ее репрезентативность | 1. Использование трудовых ресурсов (использование рабочего времени). 2. Использование основных фондов (использование времени работы оборудования). 3. Использование оборотных средств (производственных запасов, объема незавершенного производства). 4. Использование материальных ресурсов (выполнение плана материально-технического снабжения). 5. Анализ организационно-технического уровня (качества выпускаемой продукции, эффективность внедрения новой техники) |
| 2. Дифференциальное и интегральное исчисление | В основе дифференциального способа определения влияния различных факторов на результативный показатель лежит метод нахождения полного дифференциала функции многих переменных. В методе дифференциального исчисления предполагается, что общее приращение функций (результативного показателя) разлагается на слагаемые, где значения каждого из них определяется как произведение соответствующей частной производной на приращение переменной, по которой вычислена данная производная. Интегральный метод позволяет избежать в отличии от дифференциального исчисления – неразложимого остатка, так как он основывается на интегрировании приращений результативного показателя по не которой линии, соединяющей базовое и текущее значение влияющих факторов. | 1. Анализ использования трудовых ресурсов (анализ влияния различных факторов на выработку одного рабочего). 2. Анализ себестоимости продукции (влияние различных факторов на затраты по управлению и обслуживанию производством). 3.. Анализ прибыли, рентабельности, производительности труда, использования основных производственных фондов - в части оценки влияния факторов, зависящих от предприятий объединения. 4. Анализ внедрения новой техники, в частности при анализе фактической эффективности по мероприятиям, не поддающимся строгому количественному учету (внедрение новой системы планирования, учета, стимулирования и т.п.) и др. |
| Метод | Сущность метода | Сфера применения в экономическом анализе |
| 3. Анализ вариационных рядов распределения | Сущность анализа вариационных рядов распределения состоит в том, чтобы выявить закономерность распределения и определить ее характер. Закономерности распределения наиболее отчетливо проявляются только при массовом наблюдении | 1. Анализ вариационных рядов распределения, позволяет выявить закономерности распределения, обосновать гипотезу о соответствии закону нормальному распределению. 2. Характеристика абсолютных и относительных показателей вариации. 3. Характеристика основных закономерностей распределения. 4. Оценка структуры распределения совокупности. 5. Построение теоретическое распределение, соответствующего закону нормального распределения |
| 4. Методы изучения многомерных совокупностей | Сущность данных методов состоит в комплексном применении корреляционного, регрессионного, дисперсионного анализа, проведение кластерного анализа, построение ковариационных и спектральных таблиц и графиков, компонентный, факторный анализ Связь считается корреляционной, если среднее значение одного показателя меняется на какую-то величину при изменении другого. Позволяет количественно оценивать связи между большими числами взаимодействующих экономических явлений. Его применение делает возможным проверку различных экономических гипотез о наличии и силе связи между двумя явлениями или между отдельным явлением и группой их Задача дисперсионного анализа - оценить соотношение между факторами для определения существенности или несущественности различия условий наблюдения | 1. Выявляется зависимость между факторными и результативным признаками в изучаемой совокупности предприятий. 2. Определение форм зависимости между анализируемыми показателями 3. По выбранному спектру показателей строятся аналитические группировки изучаемой совокупности предприятий 4. Анализируется влияние отдельных компонентов на результативный показатель 5. При изучении изменения качественных показателей, три исследовании различий в уровнях показателей при межзаводском анализе |
| Метод | Сущность метода | Сфера применения в экономическом анализе |
| 5. Эконометрические методы | Эконометрические методы строятся на синтезе трех областей знаний: экономики, математики и статистики. Основой эконометрики является экономическая модель, под которой понимается схематическое представление экономического явления или процесса с помощью научной абстракции, отражения их характерных черт. | 1. Матричные (балансовые модели, строящиеся по шахматной схеме и позволяющие в наиболее компактной форме представить взаимосвязь затрат и результатов производства. 2. Производственные функции позволяют исследовать функциональные зависимости между затратами ресурсов и выпуском продукции. 3. Региональный и пространственный анализ, позволяет исследовать размещение и концентрацию производства в регионах. 4.Теория экономического роста, обосновывает варианты достижения планируемой ситуации, при оптимальном использовании ресурсов 5. Система национальных счетов - современная система информации, используемая практически во всех странах для описания и анализа развития рыночной экономики на макроуровне. |
| 6. Линейное программирование | Метод, заключающийся в нахождении экстремальных (максимальных или минимальных) значений линейной функции многих переменных при наличии линейных ограничений | 1. Использование основных фондов (резервы, связанные с оптимизацией загрузки оборудования). 2. Использование оборотных средств (сокращение отходов при раскрое, рациональное использование отходов). 3. Затраты по управлению и обслуживанию производством (затрат на транспортировку) 4. Обоснование оптимальной программы производства с использованием симплекс-метода, учитывающей критерий оптимальности заданной при определении данной программы. 5. Транспортные задачи, для решения минимизации грузооборота при доставке товаров от производителя к потребителю |
| 7.Нелинейное и динамическое программирование | Основывается на решении уравнений, которые характеризуются не линейными зависимостями Признаками нелинейности является, в частности, наличие переменных, у которых показатель степени отличается от единицы, а также наличие переменной в показателе степени, под корнем, под знаком логарифма. | 1. Решение задач, когда нарушаются закономерности развития, например, экономическая рентабельность не зависит от изменения масштаба производства, затраты по транспортировке изменяются в не зависимости от размера перевозимых грузов и т.п. 2. Наполняемость транспортных средств различным ассортиментом товаров, чтобы стоимость была максимальной и т.п. |
| Метод | Сущность метода | Сфера применения в экономическом анализе |
| 8.Теория управления запасами | Теория, исследующая и разрабатывающая методы расчета оптимального уровня производства или запасов, обеспечивающего будущие потребности (спрос) | 1. Анализ материально-технического снабжения (установление норм запасов сырья, материалов, а также объема незавершенного производства). 2. Анализ реализации товарной продукции (размеров готовой продукции на складе и товаров отгруженных) |
| 9. Сетевые методы | Метод изучения определенной взаимосвязанной совокупности работ в специфической форме сети, позволяющей четко определить временные взаимосвязи работ | 1. Анализ организационно-технического уровня производства (технической подготовки производства, сроков внедрения новой техники). 2. Анализ основных фондов (анализ их ввода, реконструкции, предприятия) |
| 10. Теория массового обслуживания | Прикладная область теории случайных процессов, предметом которой являются вероятностные модели физических систем обслуживания, в которых в определенные моменты времени возникают заявки на обслуживание и имеются устройства для обслуживания этих заявок | 1. При анализе производительности труда (в организациях, где широко применяется многостаночное обслуживание). 2. При анализе организационно-технического уровня (организации производства, технического контроля и т.п.) |
| 11. Теория игр | Теория математических моделей, применяемая для нахождения оптимальных решений в условиях конфликта (разногласия) или неопределенности. В качестве конфликта может рассматриваться любое разногласие. Действующие в конфликте стороны называются коалициями действия | В разделе анализа реализации продукции в объединениях легкой и пищевой промышленности, реализации товаров культурно-бытового назначения |
| 12. Методы экономической кибернетики | экономическая кибернетика - системный анализ экономики. Численный метод математического моделирования, который заключается в имитации производственных процессов на ЭВМ путем воспроизведения элементарных явлений и актов процесса в последовательности, отражающей реальные связи и взаимосвязи | 1. Теория экономической информации 2. Теория управляющих систем 3. Анализ финансового состояния (изучение общей модели финансовых взаимоотношений объединения с бюджетом, министерством, поставщиками, покупателями). 4. Анализ организационно-технического уровня (качества продукции, сложной в изготовлении; разработки и внедрения автоматизированных систем управления) |
Пример 1.
Экономико-математическая поставка задачи
Фирма может выпускать четыре вида продукции, используя для этого три вида ресурсов: трудовой потенциал, материалы и оборудование. Известны нормы расхода ресурсов на единицу продукции, наличие каждого ресурса, а также прибыль от реализации единицы продукции (табл. 6.2.). Требуется определить производственную программу, обеспечивающую максимум прибыли от реализации продукции.
Таблица 4.2.
Исходная информация для решения задачи
| Вид ресурса | Ед.изм. | Норма затрат ресурса на единицу продукции | Наличие ресурса | |||
| А | В | С | D | |||
| Труд Материалы Оборудование Прибыль на ед. продукции | чел-ч кг станко-ч тыс.руб. |
Построим экономико-математическую модель сформированной выше задачи. Введем обозначения:
j – индекс вида продукции;
i – индекс вида ресурса;
aij – норма затрат i-го ресурса на производство единицы j-й продукции;
bi – наличие (лимит) i-го ресурса;
pj – прибыль от реализации единицы j-й продукции;
xj – объем выпуска j-й продукции.
1. Ресурсные ограничения
2х1 + 2х2 + 1х3 + 2х4 £ 250
4х1 + 5х2 + 3х3 + 6х4 £ 600
1х1 + 1х2 + 2х3 + 1х4 £ 200
Расход ресурсов в производстве не может превышать их наличия.
2. Условия не отрицательности переменных:
х1 ³ 0;
x2 ³ 0;
x3 ³ 0;
x4 ³ 0.
Продукт может либо производиться в некотором количестве, т.е. xj>0, либо не производиться, тогда xj = 0.
3. Критерий оптимальности:
5х1 + 3х2 + 4х3 + 2х4 ® max
Максимизируется прибыль от реализации продукции.
Запись задачи в канонической форме
Наиболее распространенным методом решения задач линейного программирования является симплексный метод. Для решения задачи.симплексным методом исходную экономико-математическую модель необходимо привести к каноническому виду. Общая математическая запись задачи линейного программирования в канонической форме имеет вид:
åaij = bi, i = 1,2, …, n; (4)
xj ³ 0, j = 1,2,…,n, n+1,…n+m; (5)
åpjxj ®max. (6)
При записи задачи в каноническом виде ограничения (4) необходимо представить в форме строгих равенств, а выражение экстремума целевой функции (6) — в виде максимума. Ограничения неравенства исходной модели приводятся к равенствам путем введения дополнительных переменных (в ограничения типа вводятся дополнительные переменные с положительными единичными коэффициентами, а в ограничения типа - с отрицательными единичными коэффициентами). На дополнительные переменные накладывается условие не отрицательности, а коэффициенты целевой функции при них принимаются равными нулю. Если исходная модель имеет целевую функцию на минимум, то знаки при коэффициентах в ней меняются па противоположные.
Экономико-математическая модель рассматриваемой задачи в канонической форме будет иметь следующий вид:
2х1 + 2х2 + 1х3 + 2х4 + 1х5 + 0х6 + 0х7 = 250 (7)
4х1 + 5х2 + 3х3 + 6х4 + 0х5 + 1х6 + 0х7 = 600
1х1 + 1х2 + 2х3 + 1х4 + 0х5 + 0х6 + 1х7 = 200
х1 ³0; (8)
х2 ³0;
х3 ³0;
х4 ³0;
х5 ³0;
х6 ³0;
х7 ³ 0;
5х1 + 3х2 + 4х3 + 2х4 + 0х5 + 0х6 + 0х7 ®max.
Экономический смысл дополнительных переменных задач
В ресурсных ограничениях (4) задачи в каноническом виде правая, часть условия означает наличие (лимит) ресурса на предприятии, а сумма первых четырех слагаемых левой части, соответствующих основным переменным задачи, — расход ресурса, производстве, который может либо совпадать с его наличием, либо быть меньше. В случае превышения наличия ресурса на предприятии над его фактическим использованием в производстве продуктов дополнительные переменные отражают недоиспользованный объем ресурса. Таким образом, рассматриваемые ресурсные уравнения по своей сути представляют балансовые равенства:
использованный ресурс + неиспользованные ресурсы + наличие ресурса
В нашей задаче дополнительные переменные можно интерпретировать следующим образом:
х5 – недоиспользованный фонд рабочего времени, чел. –ч.
х6 – недоиспользованный объем материалов, кг
х7 — недоиспользованный фонд станочного времени, станко-ч.
На дополнительные переменные (как и на основные) накладывается условие не отрицательности (9), так как если ресурс используется полностью, дополнительная переменная будет равна нулю, если ресурс недоиспользуется, то дополнительная переменная примет положительное значение.
В целевой функции дополнительные переменные имеют нулевые коэффициенты, так как неиспользованные остатки ресурсов не участвуют в создании продукта, а следовательно, и в создании прибыли.
Анализ симплексного метода решения задачи
Решение задачи симплекс-методом осуществляется путем ряда итерации, состоящих в последовательном улучшении допустимого решения. Каждой итерации соответствует своя симплексная таблица. Оптимальный план содержится в последней симплексной таблице. Решение поэтапно представлено в табл. 4.3 – 4.5.
Таблица 4.3.
Симплексная таблица первого плана задачи
| Pi | Бх | X0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | |
| Х5 Х6 Х7 J | -5 | -3 | -4 | -2 |
Таблица 4.4.
Симплексная таблица второго плана задачи
| Pi | Бх | X0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | |
| Х1 Х6 Х7 J | Ѕ 3/2 -3/2 | Ѕ -2 -1/2 5/2 |
Таблица 4.5.
Симплексная таблица оптимального решения задачи
| Pi | Бх | X0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 |
| Х1 Х6 Х3 J | 2/3 -5/3 -1/3 | -1/3 -2/3 2/3 |
В каждой из таблиц во втором столбце (Бх) указаны базисные неизвестные. Неизвестные, не входящие в базис, на данном шаге равны пулю. Значения базисных неизвестных записаны в третьем столбце (Хо). Нижний элемент этого столбца является значением критерия оптимальности на данном шаге. В первом столбце (Рj) представлены коэффициенты при базисных неизвестных, взятые из критерия оптимальности. Каждый из столбцов Х1 – Х4 соответствует основным переменным задачи, а столбцов Х5 –Х7 — дополнительным переменным задачи. Последние элементы этих столбцов образуют нижнюю строку, содержащую элементы. С их помощью определяется, достигнут ли оптимум, а если не достигнут, то какое небазисное неизвестное следует ввести в базис, чтобы улучшить план. Элементы последнего столбца (9) позволяют найти то из прежних базисных неизвестных, которое следует вывести из базиса, чтобы улучшить план. Разрешающий элемент, расположенный на пересечении столбца, вводимого в базис неизвестного, и строки неизвестного, выводного из базиса, отмечен в каждой таблице символом “•”
Рассмотрим первую симплексную таблицу решения задачи.
1. План задачи находится в столбцах Бх и Хо
Х5 = 250 (объем неиспользованных трудовых ресурсов, чел-ч);
Х6 = 600 (объем неиспользованных материалов, кг);
X7 = 200 (объем неиспользованного оборудования, станко-ч).
По начальному плану неиспользованные остатки всех ресурсов на предприятии равны их полному объему, поэтому производство продукции А,В, С, D равно нулю (Х1-Х4 в базис не вошли).
2. Информация, содержащаяся в столбцах Х1 – Х7.
Элементы столбцов Х1 – Х7 являются коэффициентами замещения неизвестных. Они показывают, в каком соотношении любые из н6еизвестных могут заменить базисные переменные в плане данного шага.
Так, стоящий на пересечении строки Х5 и столбца Х1 элемент 2 является нормой затрат трудовых ресурсов (чел.-ч) на единицу продукции А. Таким образом, производство единицы продукции А (неизвестное X1) уменьшит неиспользованный остаток трудовых ресурсов (неизвестное X5) на 2 чел.-ч. Аналогично производство единицы продукции А заменит из плана 4кг неиспользованного остатка материалов и 1 станко-ч недоиспользованного фонда станочного времени.
В столбцах Х2 – Х4 находятсякоэффициенты замещения по продуктам В, С и D.
Нули в столбцах дополнительных переменных Х5 — Х7 указывают, что неиспользованные остатки ресурсов друг друга не заменяют, а единицы характеризуют замену базисных неизвестных самих на себя, т.е. введение в базис единицы неиспользованного ресурса вытесняет единицу этого неиспользованного ресурса.
3. Элементы нижней строки (J).
Элементы нижней строки столбцов Х1 – Х7 показывают размер уменьшения значения критерия оптимальности от замены базисных неизвестных Хj
Показатель рассчитывается перемножением элемента первого столбца таблицы (Рj) на элемент столбца Xj с последующим вычитанием соответствующего элемента Рj, т.е. показатель (столбец Хj) был рассчитан следующим образом:
0 х 2+0 х 4+0 х 1-5= -5.
Сумма трех произведений левой части подученного выражения показывает уменьшение первоначальной (нулевой) суммарной прибыли фирмы за счет вытеснения из плана (уменьшения) неиспользованных 2 чел.-ч трудовых ресурсов; 4 кг материалов и 1 станко-ч оборудования, обусловленных производством единицы продукции А. Это увеличит (т.е. даст отрицательное уменьшение) прибыль на 5 тыс. руб.
Наличие отрицательных свидетельствует о том, что найденный план производства не является оптимальным, так как имеются возможности увеличения прибыли.
По рассчитанным значениям можно судить о том, что в базис (план производства) следующего шага (см. табл. 6.4.) целесообразно ввести неизвестное Х1 (продукция А), так как производство единицы продукции А увеличит значение критерия оптимальности (прибыль предприятия) на 5 тыс.руб. (Р1) против 3 тыс.руб. при производстве продукции В (Р2), 4 тыс.руб. – продукции С (Р3) и 2 тыс.руб. – продукции D (Р4).
Какое из первоначальных базисных переменных заменит вектор Х1?
4. Элементы последнего столбца (0) таблицы
Для определения неизвестного, которое необходимо вывести из базиса, используют показатели последнего столбца 0. Он получен путем деления элемента третьего столбца Хо на элемент столбца Х, (неизвестное, вводимое в базис следующего шага), т.е. неиспользованные остатки ресурсов делим на коэффициенты замещения. Так как в плане первого шага все ресурсы полностью не используются, то каждый из элементов последнего столбца показывает, сколько продукции А можно изготовить за счет полного использования соответствующего ресурса. Но производство продукции А требует одновременной затраты всех трех ресурсов, в случае полного использования одного из ресурсов дальнейшее-производство продукции становится невозможным. Параметр 9 показывает, какой ресурс нас лимитирует, поэтому выводим из базиса переменную, соответствующую наименьшему положительному значению 9. Рассматривая значения последнего столбца (табл. 6.3), можно заключить, что производство продукции А возможно лишь в объеме 123 шт. При данном объеме производства будут полностью использованы трудовые ресурсы в размере 250 чел.-ч, а недоиспользованный остаток Х5 станет нулевым.
Итак, итог анализа симплексной табл. 6.3. - план не является оптимальным, необходимо улучшить его путем замены в базисе неизвестного Х5 на неизвестное X1.
Показатели строки X1, (см. табл. 6.4.) следующего шага решения получены путем деления элемента разрешающей строки X5; (табл. 6.3.) первого шага на разрешающий элемент 2 (отмечен в таблице символом, “*”). Например, коэффициент замещения продукта С на продукт А равен 1/2: 1 чел.-ч/шт. продукта А: 2 чел.-ч/шт. продукта С = 1/2 шт. продукта С/шт. продукта А.
В плане второго шага производство единицы продукта С вытеснит производство продукции А на 1/2 шт. Действительно (см. табл.6.3.), если производство продукции С уменьшало неиспользованные трудовые ресурсы на 1 чел.-ч, а единица: продукции А —на 2 чел-ч., то с точки зрения использования трудовых, ресурсов их взаимный коэффициент замещения равен 1/2;
Базисными переменными второго шага явились Х1, Х6, Х7(см. табл. 6.4.).По найденному решению, предприятие может выпускать 125 продукции А (Х1=125), при этом трудовые ресурсы будут использованы полностью (Х5=0), остаток неиспользованных материалов составит 100 кг (Х6=100), остаток недоиспользованного оборудования - 75 станко-ч, (Х7=75). Такая производственная программа даетпредприятию 625 тыс. руб. прибыли.
Как видно, величины неиспользованного остатка материалов [600-(250/2)*4=100] и оборудования [200-(250/2)*1=75] в плане второго шага уменьшились, так как производство 125 шт. продукции А (250:2 = 125) требует 500 кг материалов (125х4 = 500), 125 станко-ч оборудования (125х1= 125).
Увеличение с -4 (табл. 6.3.) до -3/2 (табл. 6.4.) показывает, что включение в план продукта С еще выгодно (5х1/2 + 0х1 + + 0х3/2 - 4 = -3/2), по в меньшей степени, чем на первом шаге. Теперь производство единицы продукта С, приносящее предприятию 4 тыс. руб. прибыли, возможно лишь при замещении 1/2 шт. продукта А (в силу полного использования трудовых ресурсов, (Х5=0). Появление в плане единицы изделия С (Х3) уменьшит неиспользованные остатки материалов на 1 кг (Х6) и фонда станочного времени на 3/2 станко-ч (Х7).
Наличие на втором шаге единственного отрицательного ** свидетельствует о том, что в базис нужно ввести Х3. Как видноизстолбца 0, Х3 заменит в базисе Х7. Обратимся к оптимальному плану.
Содержание симплексной таблицы оптимального решения задачи
Оптимальное решение задачи содержится в табл. 6.5. Проанализируем таблицу.
1. Оптимальный план прямой задачинаходится в столбцах Бх и Хо (здесь и далее оптимальное решениеотмечено звездочкой):
X1* = 100 (объем производства продукции А, шт.);
Х3* = 50 (объем производства продукции С, шт.);
Х6* = 50 (объем недоиспользованных материалов, кг);
3. Оптимальный план двойственной задачи находится в нижней строке в столбцах, соответствующих дополнительным переменным:
u1* = 2 (двойственная оценка трудовых ресурсов, столбец Х5);
u2* = 0 (двойственная оценка материалов, столбец Х6);
u3* = 1 (двойственная оценка оборудования, столбец Х7).
5. Элементы нижней строки таблицы.
В нижней строке таблицы в столбцах Х1-Х4 находятся коэффициенты Dj, показывающие, насколько уменьшится прибыль при увеличении значения соответствующей переменной на единицу.
Так, выпуск единицы не вошедших в оптимальный план продуктов В и D уменьшит прибыль предприятия соответственно на 3 тыс. руб. (D2) и 2 тыс. руб. (D4).
В нижней строке в столбцах Х5-Х7 находятся переменные ui, показывающие, насколько изменится прибыль (Df) при изменении дефицитного ресурса на единицу (Dbi). Увеличение на единицу дополнительных переменных Х5-Х7 означает прирост неиспользованных остатков соответствующих ресурсов. Если в оптимальном плане ресурс используется полностью, то дополнительная переменная равна нулю (в нашей задаче X5* = 0 и Х7* = 0), и введение Dxn+1 = 1 будет означать уменьшение расхода i-го дефицитного ресурса в производстве на единицу (Dbi = -1). Естественно, что это вызовет уменьшение прибыли. Так, сократив фонд рабочего времени на 1 чел.-ч (X5 = 1, пли, что то же самое, Dbi = -1), предприятие потеряет 2 тыс. руб. прибыли. Если произойдет уменьшение фонда рабочего времени на 3 чел.-ч (Dbi = -3), то предприятие потеряет б тыс. руб. прибыли:
Df(х) = (2 тыс.руб./чел.-ч) х 3 чел.-ч = 6 тыс. руб.
Аналогично увеличение объема дефицитного ресурса будет вести к росту прибыли. Увеличим, к примеру, фонд рабочего времени на 2 чел.-ч, а фонд станочного времени на 4 станко-ч, тогда прирост прибыли составит 8 тыс. руб.:
Df(х) = (2 тыс. руб./чел.-ч) х 2 чел.-ч + (1 тыс. руб./станко-ч) х х 4 станко-ч = 8 тыс. руб.
На основании данных нижней строки можно установить оптимальность варианта плана, представленного в симплексной таблице. Если все коэффициенты нижней строки неотрицательны, то план оптимален, так как увеличение любой переменной приведет лишь к.уменьшению целевой функции. Таким образом, все возможности улучшения плана исчерпаны.
4. Информация, содержащаяся в столбцах основных переменных (Х1-Х4), позволяет определить, насколькоуменьшатьсязначения базисных переменных (перечисленных в столбце Бх), прибыль (нижняя строка), если соответствующую переменную увеличить на единицу. Так, если включить в план единицу продукта В(Dx2 = 1),то придется на единицу сократить выпуск продукта А, выпуск продукта С при этом не изменится, а недоиспользование материалов (переменная Х6) уменьшится на 1 кг (т.е. материалы будут использоваться полнее). Прибыль же при этом сократиться на 2 тыс.руб.
Это уменьшение прибыли может подтвердить также следующий расчет. Уменьшение выпуска продукции А на единицу приведет к сокращению прибыли на 5 тыс. руб. (5х1 = 5). Увеличение же выпуска продукта В на единицу даст 3 тыс. руб. прибыли. Итого, изменение прибыли составит -2 тыс. руб. (Df = 3-5 = -2). Таким образом, выпуск продукта В при заданных условиях невыгоден предприятию.
Последствия изменения выпуска продукта D показаны соответственно в столбце Х4. Посмотрим, что произойдет, если в план включить 5 единиц этого продукта. Выпуск продукта А при этом уменьшится на 5 шт. (1х5 = 5), выпуск продукта С не изменится (1х5 = 0), материалы же будут использоваться полнее на 10 кг (2х5 = 10). В результате прибыль уменьшится на 15 тыс. руб. (3х5 = 15), т.е. план станет хуже оптимального.
5. Информация, содержащаяся в столбцах дополнительных переменных (Х5-Х7). характеризует изменение величины базисных переменных (Хj) и прибыли (Рj) при изменении на единицу соответствующей дополнительной переменной. Так, коэффициенты столбца X7 (не доиспользование оборудования) показывают, что при увеличении фонда станочного времени на 1 станко-ч выпуск продукции А (X1) сократится на 1/3 шт., а продукции С (X3) увеличится на 2/3 шт.; при этом не доиспользование материалов (Х6) уменьшится на 2/3 кг (т.е. материалы будут использоваться полнее), а прибыль возрастет на 1 тыс. руб.
Рассмотрим, что произойдет, если увеличить фонд рабочего времени предприятия, к примеру, на 3 чел.-ч (Dbi = 3, или, Dx5 = -3). На основании данных столбца Х5 получим:
D Х1 = 2/3 х 3 = 2 (выпуск продукта Аувеличится на 2 шт.);
DХ3 = 1/3 х 3 = -1 (выпуск продукта С уменьшится на 1 шт. );
DХ4 = -5/3*3 = -5 (расход материалов в производстве увеличится на 5 кг, так как на эту.величину уменьшилось их не доиспользование);
Df(х) = 2*3 = 6 (прибыль вырастет на 6 тыс.руб.)
Таким образом, предприятию выгодно добиваться увеличения трудовых ресурсов.
На основании произведенного расчета нетрудно определить новую программу выпуска продукции по формуле Хj = Хjн + ** Хj.
Используя данную формулу, получим:
Х1н = 100 + 2 = 102
Х3н = 50 – 1 = 49.
Значение критерия оптимальности (прибыль) можно определить двумя путями: или на основе рассчитанного приращения прибыли (fн(х) = f(х) + Df(х) = 700 + 6 = 706), или по новой производственной программе (fн(х) = åpjxнj = 5 х 102 + 4 х 49 = 706).
Можно проверить также расход материалов на новую производственную программу. На основании заданных норм расхода (см. табл. 6.2.) получим: 4 х 102 + 3 х 49 = 555 кг. Это на 5 кг больше, чем при первом варианте оптимального плана, что соответствует расчетам, проведенным по данным столбца Х5. Объем же неиспользованных материальных ресурсов соответственно уменьшится на 5 кг: X6н = 600 - 555 = 45 вместо Х6* = 50.
Таким образом, информация, содержащаяся в столбцах дополнительных переменных симплексной таблицы оптимального решения задачи, позволяет определить сдвиги в производственной программе при изменении объемов ресурсов.
Однако необходимо иметь в виду, что этот метод можно использовать лишь при незначительных изменениях объемов ресурсов, которые не ведут к изменению самого набора переменных, сходящих в базис оптимального плана. Если в результате расчетов появится хотя бы одно Xj < 0 (независимо от того, основная или дополнительная это переменная), то план стал недопустимым и задача должна быть решена заново.
Теория очередей. Основы знаний об очередях, иногда называемыетеорией очередей или теорией массового обслуживания, составляют важную часть теории управления производством. Анализ очередей в терминах длины очередей, среднего времени ожидания и других факторов помогает нам лучше понять системы обслуживания.
Менеджер оценивает изменения, возникающие в затратах, связанных с обеспечением хорошего обслуживания, и в затратах, связанных с ожиданием в очереди клиента или машины. Он может предложить увеличить время ожидания, если соблюдается баланс между количеством продаж и затратами на обслуживание покупателей. Его задача – организовать такое обслуживание, чтобы покупатель не ушел без покупки и, если купил то не потерял бы охоту вернуться еще раз.
Характеристика систем массового обслуживания. Рассмотрим три элемента систем массового обслуживания:
1) появление заявок на входе в систему;
2) порядок прохождения очереди, или собственно система обслуживания;
3) средства обслуживания.
Характеристика входа. Входной источник, который генерирует поступление заявок в систему обслуживания, имеет три основные характеристики: число заявок на входе, режим поступления заявок в систему обслуживания и поведение клиентов.
Число заявок на входе. Число заявок (размер популяции) может считаться либо неопределенным (бесконечным), либо ограниченным (конечным). Если число клиентов, поступивших на вход от начала до любого заданного момента времени, является лишь малой частью потенциально возможного их числа, популяция на входе рассматривается как неограниченная, или бесконечная. На практике примерами неограниченных популяций могут служить автомобили, проходящие через пропускные пункты на скоростных дорогах, покупатели в супермаркете. Многие модели очередей рассматривают на входе такие неограниченные популяции.
Режим поступления в систему. Клиенты приходят в систему обслуживания в соответствии с определенным графиком (например, один пациент каждые пятнадцать минут, один студент на экзамене каждые полчаса) или появляются случайным образом.
Поступления клиентов считаются случайными, если они независимы друг от друга и точно не предсказуемы. Часто в задачах массового обслуживания число поступлений в единицу времени может быть оценено с помощью распределения вероятностей, известного как пуассоновское. При заданном темпе поступления (например, два клиента в час или четыре грузовика в минуту) дискретное распределение Пуассона описывается следующей формулой
 для х=0,1,...4, где
для х=0,1,...4, где
р(х) – вероятность х заявок;
х – число заявок в единицу времени;
z – средний темп поступления заявок;
е = 2,7183 (основание натурального логарифма).
Соответствующие вероятности нетрудно определить с помощью таблицы пуассоновского распределения. Если средний темп поступления заявок два клиента в час, то вероятность того, что в течение часа не будет ни одной заявки, равна 0,13, вероятность появления одного клиента – около 0,27, вероятность поступления двух заявок – около 0,27, три клиента в течение часа могут с вероятностью 0,18, четыре – с вероятностью около 0,09 и т. д. Вероятность того, что будет 9 или более заявок, близка к нулю. Вероятность появления заявок, близка к нулю. Вероятности появления клиентов, разумеется, не всегда подчиняются пуассоновскому распределению (они могут иметь какое-то другое распределение), и для того, чтобы убедиться, что пуассоновское распределение может служить хорошей аппроксимацией, следует проводить предварительные исследования.
Поведение клиентов. Большинство моделей очередей основывается на предположении, что каждый появляющийся клиент (человек или машина), вставший в очередь, ждет до тех пор, пока он не будет обслужен, и не переходит из одной очереди в другую. Жизнь значительно сложнее. На практике клиенты могут покинуть очередь потому, что она оказалась слишком длинной. Может возникнуть и другая ситуация – клиенты дожидаются своей очереди, но по каким - то причинам уходят не обслуженными. Эти случаи также являются предметом теории массового обслуживания, однако здесь не рассматриваются.
Характеристики очереди. Очередь является вторым компонентом теории массового обслуживания. Длина очереди может быть либо ограниченной, либо неограниченной. Очередь ограничена, если она по каким-либо причинам (например, из-за физических ограничений) не может увеличиваться до бесконечности. Это может быть, например, очередь в небольшую парикмахерскую, которая имеет ограниченное число мест для ожидания.
Рассматриваемые в данном разделе модели массового обслуживания исходят из предположения неограниченности длины очереди. Длина очереди не ограничена, если она может включать в себя сколько угодно клиентов. Например, очередь автомобилей на бензоколонке.
Вторая характеристика очередей – дисциплина очереди. Эта характеристика связана с правилом, в соответствии с которым обслуживаются клиенты. Большинство систем используют правило: первым пришел – первым ушел. В некоторых случаях, например в приемном покое больницы, в дополнение к этому правилу могут устанавливаться различные приоритеты. Пациент с инфарктом в критическом состоянии будет иметь приоритет в обслуживании по сравнению с пациентом, сломавшим палец. Порядок пуска компьютерных программ – другой пример установления приоритетов в обслуживании.
Характеристики средств обслуживания. Третий компонент систем обслуживания – средства обслуживания. Наибольший интерес представляют следующие их свойства: 1) конфигурация системы обслуживания; 2) временной режим обслуживания.
Основные конфигурации систем массового обслуживания. Системы обслуживания часто классифицируются по числу каналов обслуживания (например, по числу парикмахеров в парикмахерской) и по числу фаз обслуживания (этапов обслуживания одного клиента). Примером одноканальной системы обслуживания могут служить банк, в котором открыто одно окошко для обслуживания клиентов, или ресторан, обслуживающий клиентов в автомобилях. Если же в банке открыто несколько окошек для обслуживания и клиент ожидает в общей очереди, какое из них освободится первым, то мы имеем дело с многоканальной системой обслуживания. Большинство банков, так же как и почтовые отделения и авиакассы, сейчас являются многоканальными системами обслуживания.
Однофазными являются такие системы обслуживания, в которых клиент обслуживается в одном пункте (на одном рабочем месте) и затем покидает систему. Ресторан для обслуживания автомобилистов, в котором официант получает деньги и приносит заказ в автомобиль, является примером однофазовой системы. Тоже можно сказать и об агентстве, выдающем лицензии на вождение, где агент проводит тестирование и выдает лицензию.
Одноканальная однофазовая система

 Заявки
Заявки



Одноканальная двухфазовая система
Заявки







Трехканальная однофазовая система








 Заявки
Заявки


 Двухканальная двухфазовая система
Двухканальная двухфазовая система












 Заявки
Заявки
Однако, если в ресторане нужно сделать заказ в одном месте, оплатить его в другом и получить пищу в третьем, то мы имеем дело в многофазовой системой обслуживания. Если агентство по выдаче лицензий на вождение достаточно большое, то можно подождать в очереди для того, чтобы заполнить заявление, затем в другом месте пройти профессиональный тест и уже затем (третье место обслуживания) оплатить услуги и получить лицензию.
Распределение времени обслуживания. Режим обслуживания, так же как и режим поступления заявок, может быть либо постоянным, либо случайным. Если время обслуживания постоянно, то независимо от клиента требуется одинаковое время для обслуживания, например автомобиля. Такая ситуация может наблюдаться на автоматической мойке машин. Однако более часто встречаются ситуации, когда время обслуживания имеет случайное распределение. Во многих случаях можно предположить, что время обслуживания подчиняется экспоненциальному распределению. это предположение удобно, так же как и предположение о пуассоновском распределении числа поступающих заявок.
Параметры для оценки очередей. Модели очередей помогают менеджеру принять решения, увязывающие затраты на обслуживание с затратами, связанными с ожиданием. Наиболее часто при стоимостной оценке систем массового обслуживания используются следующие параметры:
1) среднее время, которое клиент проводит в очереди;
2) средняя длина очереди;
3) среднее время, которое клиент проводит в системе обслуживания (время ожидания плюс время обслуживания);
4) среднее число клиентов в системе обслуживания;
5) вероятность того, что система обслуживания окажется не занятой;
6) параметр занятости системы;
7) вероятность определенного числа клиентов в системе.
Модели систем массового обслуживания. В управлении производством можно использовать различные модели систем массового обслуживания. Опишем четыре наиболее часто встречающиеся в практике модели. Их характеристики даны в таблице 4.6
Таблица 4.6.
Модели систем массового обслуживания
| Модель | Название | Пример | Число каналов | Число фаз | Темп поступ-ления заявок | Темп обслу-живания | Число клиен-тов | Порядок прохож-дения очереди |
| А B C D | Простая система (М/М/I) Многока-нальная (М/М/S) Равномер. обслуживание (M/D/I) Огранич. популяция | Справочное бюро магазина Кассы аэрофлота Автоматическая автомойка Самолеты маленькой авиакомпа-нии | Один Несколь-ко Один Один | Одна Одна Одна Одна | Пуассо-новское Пуассо-новское Пуассо-новское Пуассо-новское | Экспоненциальный Экспоненциальный Экспоненциальный Экспоненциальный | Неограниченное Неограниченное Неограниченное Неограниченное | FiFo FiFo FiFo FiFo |
Все четыре модели имеют следующие общие характеристики:
1) пуассоновское распределение заявок;
2) правило - FiFo (первым пришел - первым ушел);
3) единственная фаза обслуживания.
Модель А: модель одноканальной системы массового обслуживания с пуассоновским входным потоком заявок и экспоненциальным временем обслуживания.
Наиболее часто встречаются задачи массового обслуживания с единственным каналом. В этом случае клиенты формируют единственную очередь, которая обслуживается одним рабочим местом. Предположим, что для систем этого типа выполняются следующие условия.
Заявки обслуживаются по принципу FIFO.
Среднее число заявок поступающих в единицу времени неизменно, хотя и является случайным процессом.
Темп обслуживания выше темпа поступления заявок.
Средний темп обслуживания известен, хотя время затрачиваемое на обслуживание клиентов различно и описывается экспоненциальным распределением вероятностей.
Формулы для описания модели А:
Число заявок в единицу времени: z
Число клиентов, обслуживаемых в единицу времени: b
Среднее число клиентов в системе 
Среднее время обслуживания одного клиента в системе: 
(время ожидания плюс время обслуживания).
Среднее число клиентов в очереди: 
Среднее время ожидания клиента в очереди: 
Параметр загруженности системы: 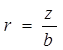
Вероятность отсутствия заявок в системе: 
Вероятность более чем k заявок в системе: 
(n - число заявок в системе).
Пример 2.
Механик автосервиса может заменить масло в трех автомобилях в течении 1 часа. Клиенты, нуждающиеся в данной услуге, приезжают в среднем по два в час, в соответствии с пуассоновским распределением. Клиенты обслуживаются в порядке прибытия, и их число не ограничено.
Решение:
z=2 машины поступают в час;
b=3 машины обслуживаются в час
 - машины в среднем в системе
- машины в среднем в системе
 - среднее время обслуживания 1 клиента в системе
- среднее время обслуживания 1 клиента в системе
 - машины в среднем ожидает в очереди
- машины в среднем ожидает в очереди
 мин – среднее время ожидания в очереди
мин – среднее время ожидания в очереди
 - процентов времени механик занят
- процентов времени механик занят
 - вероятность того, что в системе нет ни одного клиента
- вероятность того, что в системе нет ни одного клиента
После того как получены основные характеристики системы обслуживания, часто бывает полезным провести ее экономический анализ. В частности, сопоставить возрастающие затраты на улучшение обслуживания и снижающие затраты, связанные с ожиданием.
Пример 3.
Владелец автосервиса установил, что затраты, связанные с ожиданием, выражаются в снижении спроса в связи с неудовлетворенностью клиентов и равны 1000 руб за час ожидания в очереди. Заработная плата механика автосервиса составляет 70 руб в час, или 560 руб в день. Определим общие затраты.
Решение:
Так как в среднем каждая машина ожидает в очереди 2/3 часа (см. предыдущую задачу) и в день обслуживается около шестнадцати машин (2 машины в час, при 8-часовом рабочем дне), общее число часов, которое проводят в очереди все клиенты, равно

Следовательно, затраты, связанные с ожиданием, составляют
 руб в день
руб в день
Тогда общие затраты составят:
6666,66+560 = 7226,66 руб
Модель В: многоканальная система обслуживания
В многоканальной системе для обслуживания клиентов открыты два и более каналов. Предполагается, что клиенты ожидают в общей очереди и обращаются в первый освободившийся канал обслуживания. Пример такой многоканальной однофазовой системы можно увидеть в телефон-автоматах, где клиент подходит к освободившемся телефонным аппаратам. В многоканальной системе поток заявок подчиняется пуассоновскому распределению, а время обслуживания экспоненциальному. Для расчета параметров данной системы целесообразно использовать компьютерное программное обеспечение.
Модель С: модель с постоянным временем обслуживания.
Некоторые системы имеют постоянное, а не экспоненциальное время обслуживания, тогда формулы расчета будут выглядеть следующим образом:
Средняя длина очереди: 
Среднее время ожидания в очереди: 
Среднее число клиентов в системе: 
Среднее время ожидания в очереди: 
Пример 4.
Компания «ХХХ» собирает и утилизирует бытовые отходы. Водители доставляющие вторсырье ожидают в очереди на разгрузку в среднем ¼ часа. Время простоя водителя оценивается 600 руб в час. Новый компактор может обслуживать водителей при темпе 12 машин в час (или 5 мин.на одну машину). Время прибытия водителей подчиняется пуассоновскому закону с параметром z=8 водителей в час. Если приобрести новый компактор, то амортизационные затраты составят 30 руб на одного водителя контейнеровоза. Следует принять решение приобретать ли новый компактор или нет.
Решение:
1.Определим существующие затраты (без покупки компактора):

2.Определим среднее время ожидания в очереди, если будет приобретен новый компактор:

3. Определим затраты при новом компакторе:

4. Определим чистый доход от приобретения нового компактора:
150 (существующая система) – 50 (новая система) – 30 (амортизационные затраты) = 70 руб доход с одной поездки.
Модель Д: модель с ограниченной популяцией
Если число потенциальных клиентов системы обслуживания ограничено, в данном случае, чем длиннее очередь на обслуживание, тем ниже темп поступления новых заявок. Расчеты в данной модели достаточно сложны и требуют специального программного обеспечения.
4.2.3. Модели сетевой оптимизации
В математически формализованной системе анализа, планирования и управления особое место занимают сетевые графики. Они позволяют выделить из всего комплекса работ наиболее важные, лежащие на критическом пути, и сосредоточить на них основные ресурсы предприятий, устанавливать взаимосвязь между различными специализированными организациями и координировать их работу. Коммуникационная сеть минимальной длины, или дерево кратчайших расстояний, — это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети.
Пример 5.
Рассмотрим задачу регионального вычислительного центра, который должен установить специальные линии связи между пятью локальными потребителями и новым центральным компьютером. Телефонная компания берется проложить новую сеть связи. Однако организация связи — дело дорогостоящее. Чтобы сократить затраты, руководство центра решило, что общая протяженность линий связи в сети должна быть минимальной. Хотя центральный компьютер может быть связан с каждым потребителем в отдельности, более экономичным было бы установить прямую связь с частью потребителей остальных связать с центральным компьютером через потребителей, которые уже получили эту связь. Определение такой системы связи минимальной длины представляет собой пример дерева кратчайших расстояний. Сеть применительно к этой задаче с различными возможными альтернативами связи и расстояний показана на рис. 4.2.















 Рис.4.2.
Рис.4.2.
Метод, который может быть использован для решения задачи нахождения дерева кратчайших расстояний, очень прост.
Шаг 1. Начните произвольно с любого узла и соедините его ближайшим узлом. Эти два узла теперь рассматриваются как связанные узлы, а остальные — как несвязанные узлы.
Шаг 2. Определите несвязанный узел, который наиболее близок к одному из связанных узлов. Если два или более узлов можно рассматривать как ближайшие, то выберите любой из них. Добавьте этот новый узел к связанным узлам. Повторяйте этот шаг до тех пор, пока все узлы не станут связанными.
Этот сетевой алгоритм легко реализуется, если выбирать связи непосредственно на графе сети. Обращаясь к сети связи для регионального вычислительного центра и начиная с узла 1, мы находим, что ближайшим является узел 2 с расстоянием 20. Используя жирные линии для пометки дуги, обеспечивающей соединение узлов 1 и 2, мы приходим у следующему результату, характеризующему шаг 1.(рис.4.3.)
















 Рис. 4.3.
Рис. 4.3.
На втором шаге метода находим, что несвязанный узел, ближайший к одному из связанных узлов, есть узел 4 с расстоянием 30 км от узла 1. Добавляя узел 4 к множеству связанных узлов, мы получаем следующий результат (рис. 4.4.).
Повторение шага, заключающегося в добавлении ближайшего несвязанного узла к связанному сегменту сети, дает нам решение задачи о дереве кратчайших расстояний, показанное на рис. 4.5. Повторяйте шаги метода и посмотрите, получите ли вы решение. Минимальная длина дерева представлена суммой расстояний на дугах, образующих дерево.





Date: 2016-07-25; view: 601; Нарушение авторских прав