Диаграмма сдвига материала

Диаграммой сдвига материала называется зависимость между касательными напряжениями , возникающими в материале при чистом сдвиге, и соответствующими углами сдвига .

Диаграмма сдвига материала

Связь между упругими постоянными для изотропного тела

29 Кручение прямого вала поперечного сечения Определение перемещений и напряжений в поперечном сечении

Кручением называется такой вид деформации, при котором в по­перечном сечении вала возникает только крутящий момент, а все остальные внутренние силовые факторы равны нулю.

При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его проч­ности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

2) выбирают материал для рассчитываемого вала и определяют для этого ма­териала допускаемое напряжение, например по формуле (5.9), ;

3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

Для сплошного круглого сечения , отсюда можем записать вы­ражение для определения диаметра вала из условия его прочности:

Для кольцевого сечения

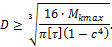
Определив размеры вала из условия прочности, проверяют вал на жесткость.

Условие жесткости требует, чтобы максимальный относительный угол закручивания , был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:

но Wp = 0,2d³, поэтому

Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала

В этой формуле допускаемый относительный угол закручивания должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения I_p будет выглядеть следующим образом:

но I_p = 0,1d ⁴ , поэтому

Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.

В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего d_вн и наружного диаметров d, т.е. при заданном параметре k = d_вн /d, формулы (5.12) и (5.13) принимают вид:

Определим крутящий момент (момент внутренних сил), возникающих в этой площадке, относительно оси кручения бруса:

М_кр = ∫_s dQ r = ∫_s τ_r dS r = ∫_s G φ₀ r dS = G φ₀ ∫_s r² dS = G φ₀ I_r,

где I_r - полярный момент инерции сечения (для круглого бруса I_r = πD⁴ / 32 = 0,1D⁴).

Из полученной зависимости найдем относительный угол закручивания: φ₀ = М_кр / (GI_r).

G - коэффициент пропорциональности между относительным углом закручивания и величиной касательного напряжения, возникающего в сечении волокна, который называют модулем упругости второго рода.

Для круга диаметром D:

W_r = I_r / 0,5D = πD⁴ / (32 x 0,5) = πD³ / 16 или приближенно: W_r ≈ 0,2D³.

Для кольца имеющего наружный диаметр D и внутренний диаметр d:

W_r = I_r / 0,5D = π(D⁴ - d⁴) / (32x0,5D) = π(D⁴ - d⁴) / 16D или приближенно: W_r ≈ 0,2(D⁴ - d⁴) / D.

Из последней формулы видно, что если полярный момент инерции кольцевого сечения можно определить, как разность между осевыми моментами инерции большого и малого кругов, то момент сопротивления кручения кольцевого сечения подобным образом рассчитать нельзя.

Итак, для определения напряжений в сечениях круглого бруса следует использовать формулы:

для сплошного вала: τ_max ≈ М_кр / 0,2D³
для трубчатого вала: τ_max ≈ М_крD / (D³ - d³)

Угол закручивания цилиндрического вала: φ = М_крl / (GI_r).

Date: 2016-07-22; view: 635; Нарушение авторских прав