
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Муравин Г.К., Муравин К.С., Муравина О.В. Алгебра. 8 класс, учебник. – 15 изд., стереотип. – М.: Дрофа, 2013. – 254 с.
|
|
33. Никольский С.М., Потапов М.К. « Алгебра» 9 класс, учебник для общеобразовательных организаций, «Просвещение» 2014.
34. Осколков В. А. и др. Сборник конкурсных задач по математике с решениями и ответами. – М.: МИФИ, 2003. – 92 с.
35. Просветов Г.И. Графики функций. – М.: Альфа-пресс, 2010.
36. Рванова А.С. Проектирование и реализация целевого и содержательного компонентов элективных курсов для классов математического профиля на основе локальной аксиометизации: автореферат дис. …кандидата педагогических наук: 13.00.02 /Рванова Алла Сергеевна; [Место защиты: Ом.гос.пед.ун-т]. – Омск, 2006. – 22с.
37. Савицкая Н. Элективные курсы в профильном обучении //Народное образование, 2004. - №6. – 275-277 с.
38. Сафонов Г. Элективные курсы в профильных классах //Народное образование, 2005. - №6. – 213-219 с.
39. Сергеев И. Н. Математика. Задачи с ответами и решениями. – М.:КДУ, 2011. – 3-е изд. – 360 с.
40. Теляковский С.А. «Алгебра» 8 класс, «Просвещение», 2008.
41. Шахмейстер А.Х. «Задачи с параметрами в ЕГЭ».С.-Петербург, 2004г.
42. Шенцева Т. А., Прудских А. Г. Элективный курс "Задачи с параметром" // Научно-методический электронный журнал «Концепт». – 2014. – Т. 12. – 191–195 с.
43. Шивринская Е.В. Задачи с параметрами как средство повышения мотивации обучения математике, 2002.- 10с.
44. Ястребинецкий Г.А. «Уравнения и неравенства с параметрами», Москва, «Просвещение», 2007.
Приложение
Решение некоторых задач:
15. При каких положительных значениях а уравнение 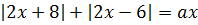 имеет одно решение?
имеет одно решение?
Решение. Нарисуем графики функций  и
и 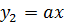 . График
. График 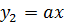 при каждом а представляет собой прямую, проходящую через начало координат.
при каждом а представляет собой прямую, проходящую через начало координат.
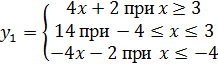
Итак, нам надо найти положительные значения а, при которых графики 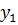 и
и 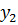 не пересекаются.
не пересекаются.
В этом месте некоторые школьники рассуждают так: Найдем а, при которых прямая 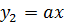 проходит через точку А (3;14) (Рис.1). Подставляя координаты точки А в
проходит через точку А (3;14) (Рис.1). Подставляя координаты точки А в 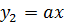 , получаем неравенство 14= а *3. Откуда а =
, получаем неравенство 14= а *3. Откуда а = 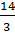 . Следовательно, при 0 < а <
. Следовательно, при 0 < а < 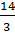 прямая
прямая 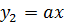 пройдет ниже точки А и решений не будет.
пройдет ниже точки А и решений не будет.

Рис.1.
Ответ: 0 < а < 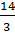
42.При каких а все решения уравнения

удовлетворяют условию х > 1.
Решение.
Случай 1. 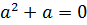 , т.е а =0 или а =-1.
, т.е а =0 или а =-1.
Рассмотрим обе эти возможности. При а =0 имеем уравнение 0* х =0, которое имеет решениями все хϵR. Следовательно, а =0 условию задачи не удовлетворяет, т.к. часть решений в этом случае ≤1.
Значение а =-1 также условию задачи не удовлетворяет, т.к. в этом случае имеем уравнение 0* х =-1, которое вообще не имеет решений.
Случай 2. а ≠0, а ≠-1. Тогда 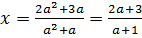 - решение уравнения. Решим неравенство х >1. Имеем
- решение уравнения. Решим неравенство х >1. Имеем

Решением последнего неравенства будут все а ϵ (-∞;-2)ᴗ (-1;+∞). Теперь нам осталось выколоть точку а =0.
Ответ: а ϵ (-∞;-2) ᴗ (-1;0) ᴗ (0;+∞).
55.Найти все значения а, при которых уравнение

имеет два решения.
При решении уравнения надо отдельно рассматривать два случая: 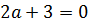 и
и  . В первом случае исходное уравнение будет линейным, во втором – квадратным.
. В первом случае исходное уравнение будет линейным, во втором – квадратным.
Решение. Случай 1. 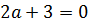 , т.е. а =-
, т.е. а =-  . Тогда уравнение имеет вид: 3 х -
. Тогда уравнение имеет вид: 3 х - 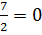 . Это уравнение имеет единственное решение х =
. Это уравнение имеет единственное решение х =  . Следовательно, а =-
. Следовательно, а =-  условию задачи не удовлетворяет.
условию задачи не удовлетворяет.
Случай 2.  , т.е. а ≠-
, т.е. а ≠-  . Тогда уравнение – квадратное. Чтобы оно имело два решения, необходимо и достаточно, чтобы его дискриминант
. Тогда уравнение – квадратное. Чтобы оно имело два решения, необходимо и достаточно, чтобы его дискриминант
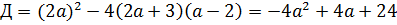 был положительным. Решая неравенство
был положительным. Решая неравенство 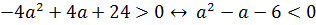 , находим а ϵ (-2;3). Теперь, выкалывая из этого промежутка точку а =-
, находим а ϵ (-2;3). Теперь, выкалывая из этого промежутка точку а =-  , получаем
, получаем
Ответ: а ϵ (-2; -  ) ᴗ (-
) ᴗ (-  ;3).
;3).
56.Найти все значения а, при которых уравнение
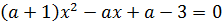
имеет не более одного решения.
Решение. Случай 1. 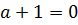 , т.е. а =-1. Тогда уравнение имеет вид
, т.е. а =-1. Тогда уравнение имеет вид 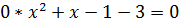 или х -4=0, которое, очевидно, имеет единственный корень х =4. Следовательно, а =-1 удовлетворяет условию задачи.
или х -4=0, которое, очевидно, имеет единственный корень х =4. Следовательно, а =-1 удовлетворяет условию задачи.
Случай 2. 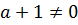 . Тогда уравнение – квадратное. Нам подходят а, при которых уравнение имеет либо один корень (тогда Д=0), либо не имеет корней (в этом случае Д<0). Итак, имеем систему
. Тогда уравнение – квадратное. Нам подходят а, при которых уравнение имеет либо один корень (тогда Д=0), либо не имеет корней (в этом случае Д<0). Итак, имеем систему
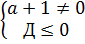
Д 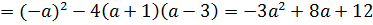 . Неравенство
. Неравенство 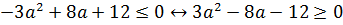 выполняется для а ϵ (-∞;
выполняется для а ϵ (-∞; 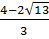 ] ᴗ[
] ᴗ[  ).
).
Учитывая значение а =-1, запишем окончательный ответ.
Ответ: а ϵ (-∞; 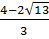 ] ᴗ[
] ᴗ[  ) и а =-1.
) и а =-1.
58.При каких значениях параметра а корни уравнения
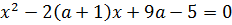
удовлетворяют неравенству х > 5?
Решение. Коэффициент при 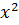 положителен, поэтому ветви параболы
положителен, поэтому ветви параболы 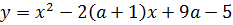 направлены вверх. Следовательно, чтобы выполнялись условия задачи, график этой параболы должен проходить относительно точки 5 как показано на рис.2, т.е. пересекать ось Ох в точках, лежащих на оси Ох правее точки 5.
направлены вверх. Следовательно, чтобы выполнялись условия задачи, график этой параболы должен проходить относительно точки 5 как показано на рис.2, т.е. пересекать ось Ох в точках, лежащих на оси Ох правее точки 5.

Рис.2.
Последнее имеет место при выполнении следующих условий
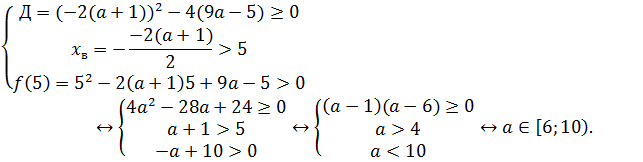
Ответ: а ϵ [6;10).
59.При каких а корни уравнения
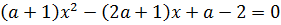
будут положительными?
Решение. Положительный корень, означает, что корни уравнения больше, чем 0. В этой задаче нельзя сразу утверждать, что наше уравнение квадратное. Это зависит от коэффициента а +1.
Случай 1. а +1=0, т.е. а =-1. Тогда уравнение принимает вид: х -3=0, откуда х =3>0. Следовательно, а =-1 удовлетворяет условию задачи.
Случай 2. а +1 > 0. Тогда, наше уравнение – квадратное, и чтобы его корни были больше нуля, график функции  должен быть расположен так, как на рис.3 а).
должен быть расположен так, как на рис.3 а).
Для этого необходимо и достаточно выполнение следующих условий
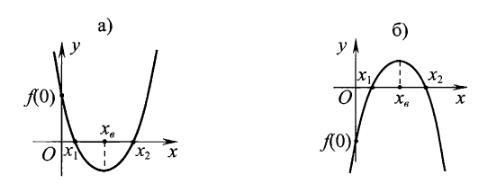
Рис.3.
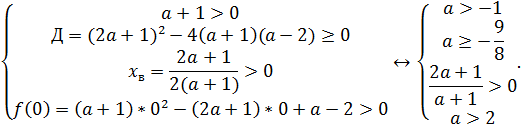
Случай 3. а +1 < 0. Тогда, чтобы его корни были положительными (рис.3 б), необходимо и достаточно выполнение следующих условий:
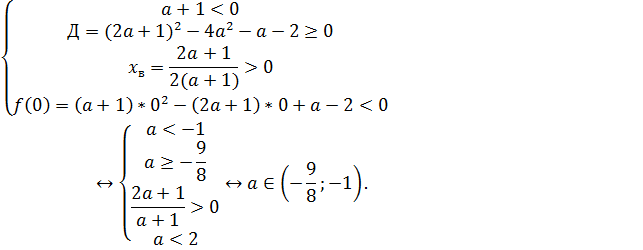
Объединив решения в случаях 1-3, получим
Ответ: а ϵ (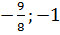 ] ᴗ (2;+∞).
] ᴗ (2;+∞).
60.При всех а решить уравнение

Решение.
Случай 1.  . В этом случае уравнение – линейное.
. В этом случае уравнение – линейное.
а) При а =1 имеем  .
.
в) При а =-1 имеем 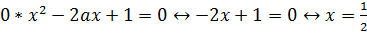 .
.
Случай 2. а ≠1, а ≠-1. Тогда исходное уравнение квадратное. Имеем, Д=  .
.
а) Если Д<0↔  то решений нет.
то решений нет.
в) Если Д>0↔ 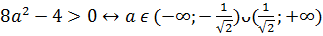 , то с учетом того, что а ≠±1, уравнение имеет два решения
, то с учетом того, что а ≠±1, уравнение имеет два решения 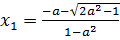 и
и 
с) Если Д=0↔  уравнение имеет один корень:
уравнение имеет один корень:
1. При  уравнение принимает вид
уравнение принимает вид 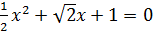 . Его единственный корень х =-
. Его единственный корень х =- 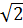 .
.
2. При 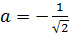 уравнение имеет вид
уравнение имеет вид  , единственный корень которого х =
, единственный корень которого х = 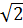 .
.
Ответ: при 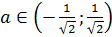 решений нет; при а =1 решение х =-
решений нет; при а =1 решение х =-  ; при а =-1 решение х =
; при а =-1 решение х =  ; при
; при  решение х =-
решение х =- 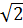 ; при
; при 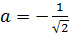 решение х =
решение х = 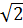 при
при  решения
решения  .
.
63.При каких а неравенство
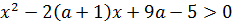
не выполняется ни для одного значения х.
Решение. Нам надо найти такие параболы, у которых ни при каком х не выполняется у > 0.
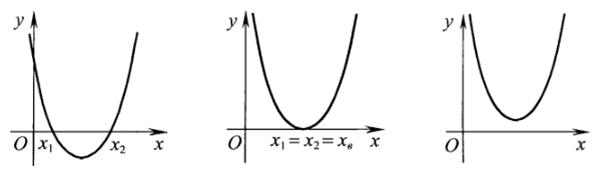
Рис.4. Рис.5. Рис.6.
Парабола на рис.4 не удовлетворяет условию задачи, т.к. при х ϵ (-∞; 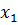 )ᴗ(
)ᴗ(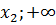 ) выполняется у > 0. Парабола на рис.5 нам также не подходит, т.к. при х ϵ (-∞;
) выполняется у > 0. Парабола на рис.5 нам также не подходит, т.к. при х ϵ (-∞;  ) ᴗ (
) ᴗ (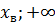 ), выполняется у > 0. И, наконец, график на рис.6 также не подходит, т.к при всех х ϵ R значение у > 0.
), выполняется у > 0. И, наконец, график на рис.6 также не подходит, т.к при всех х ϵ R значение у > 0.
Ответ: таких а нет.
64.При каких а из неравенства

выполняется при всех х, удовлетворяющих условиям 1 < х ≤ 4?
Решение. Умножив обе части неравенства на (-1), получим равносильное неравенство:
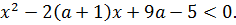
Итак, нам надо найти все а, при которых неравенство выполняется при всех х из промежутка (1;4]. Как обычно, нарисуем график квадратного трехчлена 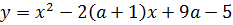 .
.
Очевидно, что нам не подходят параболы, находящиеся над осью Ох, т.к. ни при одном х не выполняется неравенство у < 0. Так же нам не подходят параболы, касающиеся оси Ох.
Из парабол, пересекающих ось Ох в двух точках, нам подходят только те, у которых промежуток (1;4] находится между корнями 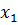 и
и  (Рис.7).
(Рис.7).
И сразу же посмотрим, подходят ли нам параболы, проходящие через точки х =1 или х =4 (рис.8 и 9).
Очевидно, что случай, изображенный на рис.8, нам не подходит, т.к. у (4)=0, а должно быть по условию задачи у (4) < 0. А случай на рис.9 нам подходит. Никакое другое расположение корней квадратного трехчлена относительно промежутка (1;4] нам не подходит.
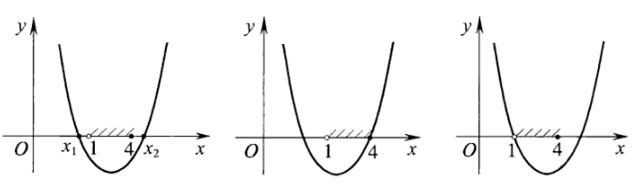
Рис.7. Рис.8. Рис.9.
Объединяя теперь случаи на рисунках, имеем систему:
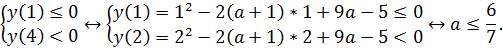
Ответ: а ϵ (-∞;  ].
].
Date: 2016-07-22; view: 513; Нарушение авторских прав