Умножение и транспонирование матриц

Определим результат операции транспонирования матрицы A размерности как матрицу размерности , элементы которой для всех и задаются следующим правилом (3)

. (3)

Таким образом, матрица

является транспонированной к матрице

Матрицы с элементами из числовых множеств, на которых определены арифметические операции сложения и умножения называются числовыми.

Определим результат операции умножения числовой матрицы A размерности справа на числовую матрицу B размерности как числовую матрицу C размерности , элементы которой для всех и задаются следующим правилом (4)

(4)

где .

Для трех произвольных числовых матриц A, B, C размерностей , , , соответственно, выполняется свойство ассоциативности (5)

. (5)

Квадратная числовая матрица размерности , элементы которой определены правилом (6)

, (6)

называется единичной.

Для произвольной числовой матрицы A размерности и единичной матрицы размерности при выполняется свойство

.

Аналогично, для произвольной числовой матрицы A размерности m 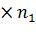и единичной матрицы размерности при выполняется свойство

.

Date: 2016-07-22; view: 404; Нарушение авторских прав