Группированная выборка

Весь интервал рахобъем на к интервалов(разрядов),подсчитаем число m,значений,попавших в каждый i интервал. Числа mi-частичными.

Поэтому, в некоторых случаях приходится рассматривать распределение случайной величины, имеющие определенные отличия от нормального. Для оценки этого отличия введены специальные характеристики. К ним относятся, в частности, асимметрия и эксцесс.Асимметрией распределения случайной величины называется отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения: .

Эксцессом распределения случайной величины называют число, определяемое выражением: .

Для нормального распределения , поэтому эксцесс равен нулю.

Вероятность попадания нормальной случайной величины в заданный интервал

Во многих практических задачах требуется определить вероятность попадания случайной величины в заданный интервал. Эта вероятность может быть выражена в виде разности функции распределения вероятности в граничных точках этого интервала:

.

В случае нормального распределения:

сделаем замену переменной: , , .

Тогда: ,

где , .

Разобьем полученный интеграл на два:

.

Следовательно, искомая вероятность может быть выражена через веденный ранее стандартный интеграл Лапласа:

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i / h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i / h.

Площадь i - го частичного прямоугольника равна hn_i / h = n_i - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению W_i / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W_i / h (Рис. 2).

Площадь i - го частичного прямоугольника равна hW_i / h = W_i - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Рис. 2. Гистограмма относительных частот

15. Метод моментов определения параметров теор.паспределения

Точечной называется оценка, которая определяется одним числом. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Интервальной называется оценка, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок (смысл этих понятий выясняется ниже).Пусть найденная по данным выборки статистическая характеристика Θ∗служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом(Θ может быть и случайной величиной). Θ∗тем точнее определяет параметр Θ,чем меньше абсолютная величина разности |Θ − Θ∗|. Другими словами, если δ > 0 и |Θ − Θ∗| < δ, то чем меньше δ, тем оценка точнее.Таким образом, положительное число δ характеризует точность оценки.Статистические методы не позволяют категорически утверждать, что оценка Θ∗ удовлетворяет неравенству |Θ − Θ∗| < δ; можно лишь говорить о вероятности γ,с которой это неравенство осуществляется.Надежностью (доверительной вероятностью) оценки Θ по Θ∗называют вероятность γ, с которой осуществляется неравенство |Θ − Θ∗| < δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0.95, 0.99 и 0.999. Пусть вероятность того, что, |Θ − Θ∗| < δ равна γ P(|Θ − Θ∗| < δ) = γ. Заменив неравенство |Θ − Θ∗| < δ | равносильным ему двойным неравенством −δ < Θ − Θ∗ < δ, или Θ∗ − δ < Θ < Θ∗ + δ, получим P(Θ∗− δ < Θ < Θ∗+ δ) = γ. Это соотношение будем понимать так: вероятность того, что интервал (Θ∗ −δ, Θ∗ + δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.Доверительным называют интервал (Θ∗ − δ, Θ∗ + δ), который покрывает неизвестный параметр с заданной надежностью γ. Интервал (Θ∗ − δ, Θ∗ + δ) имеет случайные концы (они называются доверительными границами).В разных выборках получаются различные значения Θ∗. Следовательно, от выборки к выборке будут изменяться и концы доверительного интервала, т. е. доверительные границы сами являются случайными величинами - функциями от x1, x2,..., xn. Так как случайной величиной является не оцениваемый параметр Θ, а доверительный интервал, то более правильно говорить не о вероятности попадания Θ в доверительный интервал, а о вероятности того, что доверительный интервал покроет Θ.

Интервальная оценка мат.ожидания

Дана выборка (x ₁, x ₂, …, x_n) объема n из генеральной совокупности с генеральным средним m_x (неизвестный параметр) и генеральной дисперсией s² (известна). Ищется интервал [Θ₁, Θ₂], в котором m_x может находиться с доверительной вероятностью γ. Задача может быть решена двумя путями.

I. Предполагая, что предварительно определена точечная оценка m_x – выборочное среднее , в качестве статистики для получения Θ₁ = = Θ₁(x ₁, x ₂, …, x_n) и Θ₂ = Θ₂ (x ₁, x ₂, …, x_n) традиционно рассматривается нормированное выборочное среднее

z = .

Случайная величина z имеет распределение:

1. нормальное, с нулевым математическим ожиданием и единичной дисперсией (z N (0, 1)), если выборка берется из нормальной генеральной совокупности;

2. асимптотически нормальное (z ~ N (0, 1)), если генеральная совокупность имеет распределение, отличное от нормального.

Интервальная (п.1) или асимптотическая интервальная (п.2) оценка в данном случае формируется на основе неравенства

P [ < z < ] = P [– < z < ] = γ,

откуда – δ < m_x < + δ, δ = .

Здесь – квантиль нормированного нормального распределения порядка (1 – α/2), α = 1 – γ.

Таким образом, границы доверительного интервала, найденные первым путем, могут быть определены по следующим выражениям:

Θ₁ = – ; Θ₂ = + .

II. Второй способ получения интервальных оценок в рассматриваемом случае основан на использовании выборочного среднего (без нормировки) в качестве статистики. Границы доверительного интервала определяются значениями квантилей нормального распределения N (,s²/ n ) порядков α/2 и (1 – α/2).

16. статестическая проверка гипотез

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими. Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если l является параметром экспоненциального распределения, то гипотеза Н0 о равенстве l =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве l >10 состоит из бесконечного множества простых гипотез Н0 о равенстве l =bi, где bi – любое число, большее 10. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется. Множество S0 называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.

Критерий согласия Пирсона χ² – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими (f_Т) и эмпирическими (f) частотами к теоретическим частотам:

• k–число групп, на которые разбито эмпирическое распределение,
• f_i–наблюдаемая частота признака в i-й группе,
• f_T–теоретическая частота.

Для распределения χ² составлены таблицы, где указано критическое значение критерия согласия χ² для выбранного уровня значимости α и степеней свободы df (или ν).

17. Регрессионный анализ — это статистический метод исследования зависимости случайной величины у от переменных (аргументов) х_j (j = 1, 2,..., k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения x_j.

Обычно предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием =φ(x₁,..., х_k), являющимся функцией от аргументов х_j и с постоянной, не зависящей от аргументов дисперсией σ².

Обычно предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием =φ(x₁,..., х_k), являющимся функцией от аргументов х_j и с постоянной, не зависящей от аргументов дисперсией σ². Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид

(53.8)

где β _j — параметры регрессионной модели;

ε _j — случайные ошибки наблюдения, не зависимые друг от друга, имеют нулевую среднюю и дисперсию σ².

Отметим, что модель (53.8) справедлива для всех i = 1,2,..., n, линейна относительно неизвестных параметров β₀, β₁,…, β_j, …, β_k и аргументов.

Линейные и нелинейные модели регрессии

Уравнение линейной регрессии: у = а + bx

Уравнения нелинейной регрессии

полиномиальная функция

гиперболическая функция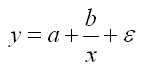

степенная модель

показательная модель экспоненциальная модель

Date: 2016-07-20; view: 2230; Нарушение авторских прав